基于改进型电流控制策略的单相并网逆变装置研究

曾晓生，杨 苹

(华南理工大学电力学院，广东省绿色能源技术重点实验室，广东广州510640)

1 引言

在风能、太阳能并网发电系统中，并网逆变装置是最为核心的部分。而控制算法的改进是优化并网逆变装置的关键。高性能的逆变器不但动态响应快，而且稳态精度高，抗干扰能力强，系统稳定。

对于单相并网逆变装置，目前广泛应用电流控制的控制方式［1］，使逆变器相当于一个电流源。闭环控制电流的方法有电流瞬时值PI控制、电流滞环控制［2］、单周控制［3］和无差拍控制［4］等。其中电流瞬时值PI控制已经是工程应用中比较成熟有效的方法，具有简单、易实现的优点，能够使并网逆变器的输出电流快速地跟踪参考电流的变化，有良好的动态性能。随着研究的不断深入，从该方法已经发展出直接电流控制、间接电流控制和混合控制等不同的策略［5］。然而，单独的电流瞬时控制环不能满足系统输出精度的要求。因此本文在电流瞬时值PI控制的基础上加入电流平均值外环，使逆变装置不但有快速的动态性能，而且有很高的电流幅值精度。同时在电流瞬时值内环加入电网电压前馈，使系统不受电网电压的影响。

2 拓扑结构和电流瞬时值内环数学模型

为了设计电流平均值外环，需要首先确定系统拓扑和建立电流瞬时值内环的控制模型。

2.1 拓扑结构

本文选用的逆变系统拓扑结构如图1所示。

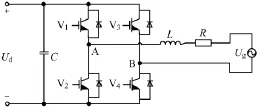
图1 系统拓扑结构Fig.1 System topology

图1中，Ud是直流母线电压，电容C起缓冲无功能量的作用，逆变电路为电压型单相全桥电路，选用IGBT作为开关管，每个开关管都并联了一个反馈二极管，为交流侧向直流侧反馈无功能量提供通道。采用单电感的滤波电路，R为滤波电感及交流进线等效阻抗。在此系统结构上，建立并网电流瞬时值控制模型。

2.2 电流瞬时值内环数学模型

由图1可以得到以下等式:

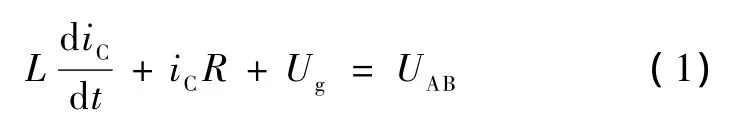
式中，L为滤波器电感;R为等效串联电阻;iC为并网电流;UAB为逆变器的输出电压;Ug为电网电压。把式(1)转化为复数域的形式并加以整理可得到滤波器的传递函数如下:

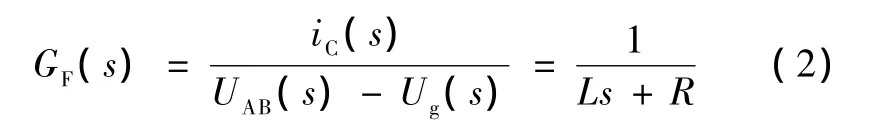
PI控制器的传递函数为［6］:

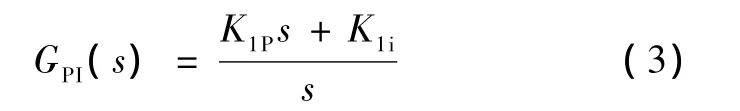
本文采用单极性的PWM控制，所以逆变环节可以等效为线性比例环节［1］，其传递函数为:

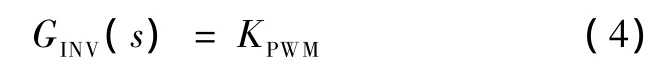
式中，KPWM数值上等于直线母线电压。

因此电流瞬时值内环的闭环传递函数:

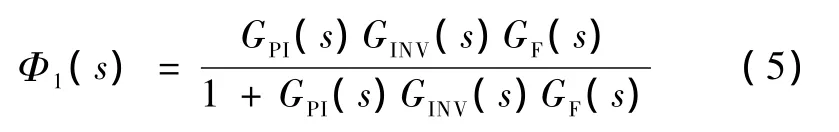
3 电流平均值外环设计

基于以上对电流瞬时值内环的分析，本节阐述平均值外环的设计。加入平均值外环后系统的控制模型如图2所示。

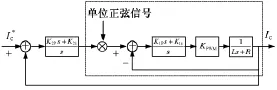
图2 加入平均值外环后系统的控制模型Fig.2 Control model with mean value loop

设计外环时，把电流瞬时值内环闭环当作被控对象。外环的输出是实际并网电流经过全波整流后在一个基波周期内算得的平均值，输入是相应的参考平均值，而外环PI控制器的输出是内环正弦参考电流的幅值。因此，图2中电流瞬时值内环，即虚线框内的部分的输入和输出都是直流量。所以，在进行外环设计时可以把图2中虚线部分的传递函数等效成一个比例系数K1，它等于内环闭环传递函数幅频特性上50Hz频率对应的增益:

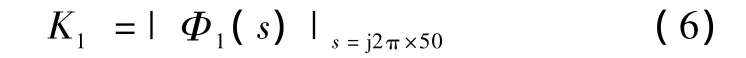
设计外环，主要是求出外环的 PI参数 K2p和K2i。设外环补偿后的穿越频率为fc，由于在穿越频率处回路的增益为1，所以有以下等式:

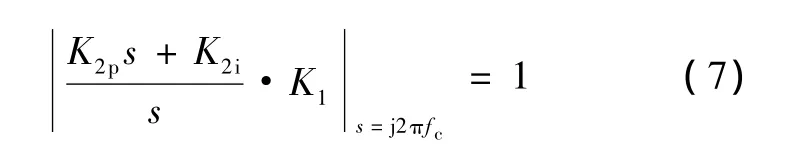
当穿越频率fc比较小时，可以使系统比较稳定，但跟踪速度慢;当fc比较大，跟踪速度快，但系统的稳定裕度下降。所以应该采用折衷的方法。

另外，在PI控制器传递函数的零点处有

式中，fz是 PI控制器零点处的频率，在本文中为100Hz。

联立式(7)和式(8)，即可算出 K2p和 K2i。于是外环的开环传递函数为

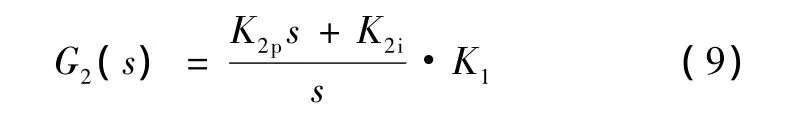
其波特图如图3所示。

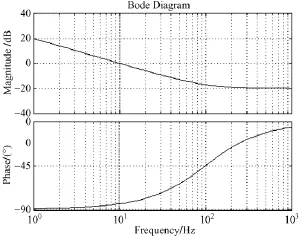
图3 外环开环传递函数波特图Fig.3 Bode diagram of outer open loop

外环的闭环传递函数为

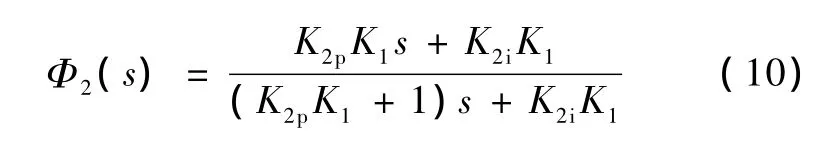
4 电网电压前馈控制

采用电流平均值和瞬时值双环控制，能使系统获得良好的动态性能和稳定精度，但无法消除电网电压的影响，所以必须在瞬时值内环加入电网电压前馈环节。加电网电压前馈后的内环控制框图如图4所示。

在图4中，如果不加电网电压前馈，可得到

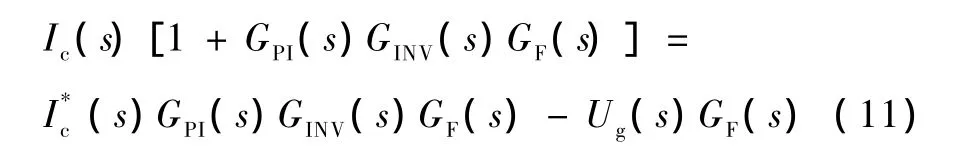
由式(11)可以看出，Ug(s)GF(s)是并网电流的干扰量。从控制理论看，电网电压可以看作系统的干扰源。

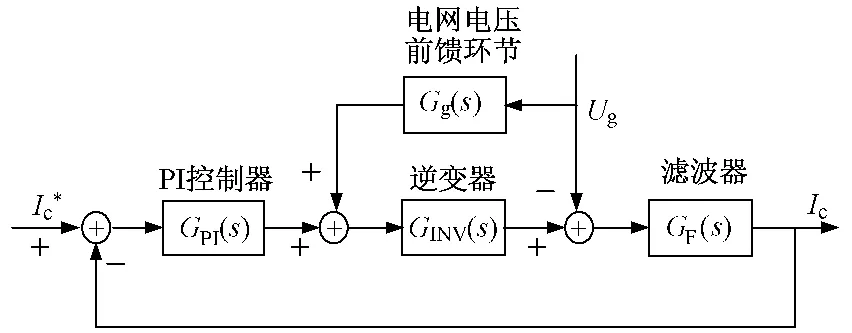
图4 加电网电压前馈后的内环控制框图Fig.4 Control block diagram with feed forward loop

如果加入电网电压前馈，由图4得到

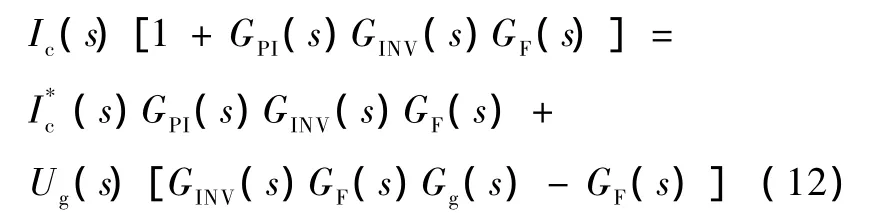
式中，若令 Gg(s)= 1/GINV(s)，可以使得Ug(s)［GINV(s)GF(s)Gg(s)－GF(s)］=0，即抵消了电网电压的影响。

5 总体控制方案

基于上文的分析，本节阐述最终的系统总体控制方案。系统在每个采样周期对并网电流瞬时值进行检测，并在一个基波周期内进行绝对值累加，然后求取平均值，与电流的参考平均值进行比较。得到的误差经外环PI调节后得到内环参考电流的幅值，再和单位正弦波相乘得到正弦参考电流。同时，系统将对电网电压过零上升沿进行捕获并以此对上述正弦电流进行锁频锁相，得到与电网电压同频同相的参考电流。该参考电流在每个开关周期的值和采样到的电流瞬时值的误差经过内环PI调节后再与电网电压前馈量相加，得到占空比，最后产生PWM信号以控制逆变电路功率开关的通断。

6 仿真与实验结果

为了证明上述控制方案的可行性，本文在Matlab环境下进行仿真验证。仿真结果如图5所示。由图可知，并网电流是和电网电压同频同相的高质量正弦波，且能很快消除幅值误差。

为了验证电流平均值外环在实际系统中能提高输出电流的幅值，本文进行了样机对比实验。实验参数:母线电压 Ud=380V，电网电压有效值 Ug=220V，给定的并网电流有效值I*rms=10A，采样频率和开关频率f=15kHz。图6和图7为实验波形图。

图6为采用电流瞬时值单环PI控制得到的实验波形。谐波总畸变率THD=4.85%，功率因数λ=0.99，输出电流有效值Irms=10.8A。可见这种情况下虽然逆变器的输出电流波形很好，但稳态误差是8%。

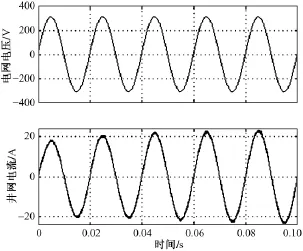
图5 仿真结果波形图Fig.5 Waveforms of simulation experiment

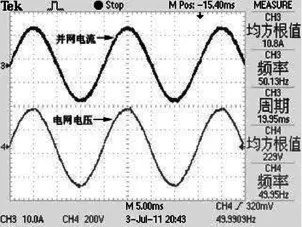
图6 电流瞬时值单环控制实验波形Fig.6 Waveforms of single loop control

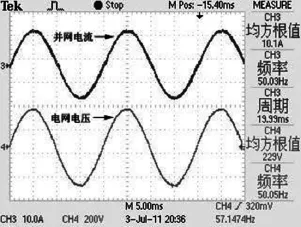
图7 电流平均值和瞬时值双环控制实验波形Fig.7 Waveforms of double loop control

图7为采用电流平均值和瞬时值双环PI控制得到的实验波形。THD=4.10%，λ=0.99，Irms=10.1A。可见所提的控制方法使系统的稳态误差降低为1%，而且电流波形为高质量的正弦波，与电网电压同频同相，不受电网电压的影响。

7 结论

本文提出了一种并网电流平均值和瞬时值双环PI控制算法，瞬时值内环使并网逆变器输出低谐波畸变率、与电网电压同频同相的正弦电流，平均值外环减小并网电流幅值的误差，提高系统的输出精度。仿真结果和样机对比实验证明了所提方法的可行性和有效性。

［1］刘伟(Liu Wei).单相光伏并网逆变数字控制策略研究与实现(Research and implementation of digital control strategy of the single phase PV grid-connected inverter)［D］.湖南:湖南大学(Hunan:Hunan University)，2007.

［2］叶齐峰，金新民(Ye Qifeng，Jin Xinmin).高功率因数脉冲整流器数字控制系统设计(Design of digital control system of the high power factor pulse rectifier)［J］.电工技术(Electronic Engineering)，2003，(1):56-57.

［3］李海林，王燕京，侯振义(Li Hailin，Wang Yanjing，Hou Zhenyi).单周控制原理及其应用(One-cycle control theory and its application)［A］.中国电工技术学会电力电子学会第十一届学术年会(The 11thAnnual Meeting of the Power Electronics Society of China Electrotechnical Society)［C］.杭州(Hangzhou)，2008.

［4］Gokhale K P，Kawamura A，Hoft R G.Deadbeat microprocessor control of PWM inverter for sinusoidal output waveform synthesis［A］.Proc.IEEE Power Electronics Specialists Conf.［C］.Toulouse，France:IEEE，1985.28-36.

［5］吴卫民，刘松培，何远彬(Wu Weimin，Liu Songpei，He Yuanbin).单相 LCL并网逆变器电流控制综述(Summarization of the current control of the single phase LCL grid-connected inverter)［J］.电源学报(Electrical Source Acta)，2011，(2):51-58.

［6］胡寿松(Hu Shousong).自动控制原理 (Principle of Automatic Control)［M］.北京:科学出版社 (Beijing:Science Press)，2001.222-226.