基于热电耦合的10kV XLPE地下电缆群温度场数值计算

王巧玲，杨玉平，梁永春

(1.河北科技大学信息科学与工程学院，河北 石家庄050018;2.河北科技大学理工学院，河北 石家庄050018;3.河北科技大学电气信息学院，河北 石家庄050018)

引言

目前电力输送大多采用地下电缆的形式，安装地下电缆需要保证地下散热条件不使电缆超温而导致绝缘损坏，但是由于影响电缆传热的可变因素很多，电缆的载流量很难准确确定。

综合目前国内外的研究现状，可将已有的电缆温度场数值计算方法概括为有限元法、边界元法、有限差分法［1-6］。对于多芯电缆，有限差分和边界元法都存在电缆区域剖分困难的问题，而有限元法可以很好地解决这个问题。

电缆导体的电阻率是温度的线性函数，而电阻率是影响电缆发热量的重要因素，同时也是本文主要考虑的，即地下电缆群温度场计算是一个热电耦合问题。本文采用有限元法进行数值计算，同时利用迭代法实现热电间接耦合，确定土壤直埋电缆的散热和周围土壤的温度分布，并最终确定电缆的载流量。

1 基本原理

1.1 损耗计算公式

单回路土壤直埋电缆如图1所示，整个区域为一个半无限大温度场。电缆群水平直埋于地下700mm处，周围填充沙土100mm，然后回填土壤。

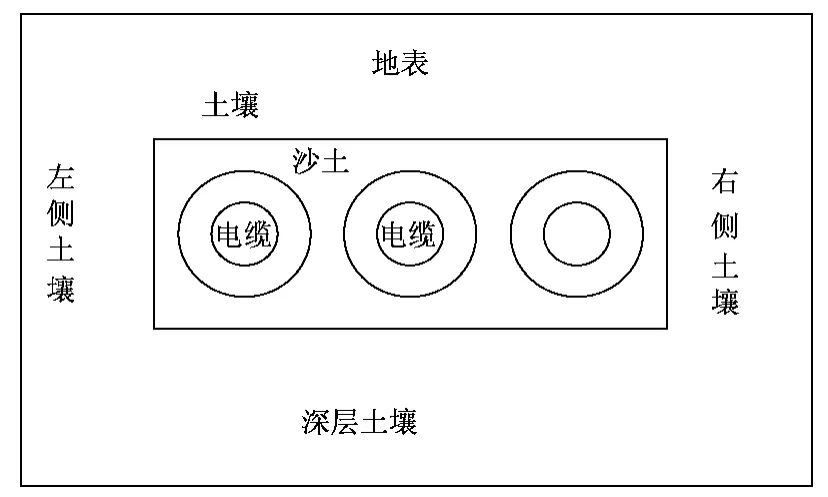
图1 土壤直埋电缆物理模型Fig.1 Physical model of underground cables

整个区域为一个半无限大温度场。需要将一个开域场转变为闭域场才能进行求解。上边界为地表，属于第三类边界。下边界、左边界和右边界可由以下方法确定。

温度仅在电缆附近变化较为剧烈，当远离电缆时，土壤温度将与环境温度相同。通常在距离电缆2000mm的土壤已不受电缆的影响。因此下边界、左边界和右边界可取距离最近电缆3000mm的直线。图1中左、右侧土壤边界为第二类边界，深层土壤边界为第一类边界。

土壤直埋电缆线芯导体损耗、金属屏蔽层损耗和铠装层损耗可以由电磁场计算而得。土壤直埋电缆的电磁场可以看作似稳场处理，且电缆截面相对于长度很小，可以看作二维场计算损耗。二维直角坐标下的涡流损耗可以描述为［7-8］:

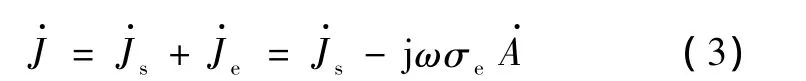
导体的损耗为:

式中，qv为单位体积内产生的热量，W/m3。

绝缘介质损耗可由IEC60287给定的公式计算。绝缘介质损耗与电压有关，每相中单位长度的绝缘损耗为:

式中，U0为对地电压(相电压)，V;tanδ为在电源系统和工作温度下绝缘损耗因数;c为单位长度电缆电容，F/m。

圆形导体电容为:

式中，ε为绝缘材料的介电常数;Di为绝缘层直径(屏蔽层除外)，mm;dc为导体直径(如有屏蔽层则包含屏蔽层)，mm。

对于10kV以下电压等级的电缆，绝缘介质损耗很小，以6/10kV 150mm2YJV22型为例，绝缘介质损耗约等于0.08W/m，在实际载流量计算中可以忽略不计。

1.2 温度场计算公式

土壤直埋电缆的稳态温度场属于二维稳态导热问题。有热源区域(如电缆导体、金属屏蔽层和铠装层)的温度控制方程为:

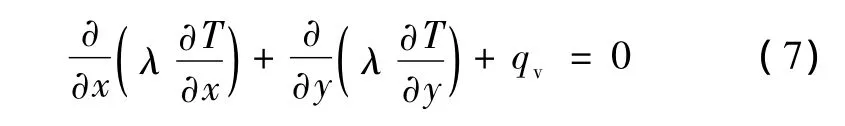
式中，T为点 (x，y)温度，℃;λ为导热系数，W/(m·℃)。

无热源区域(如电缆其他层、土壤等)的温度控制方程为:

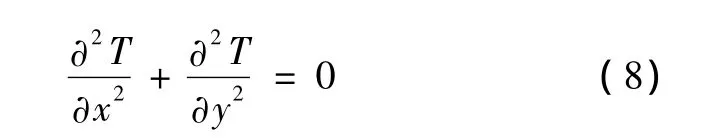
图1中的三类边界的控制方程为:

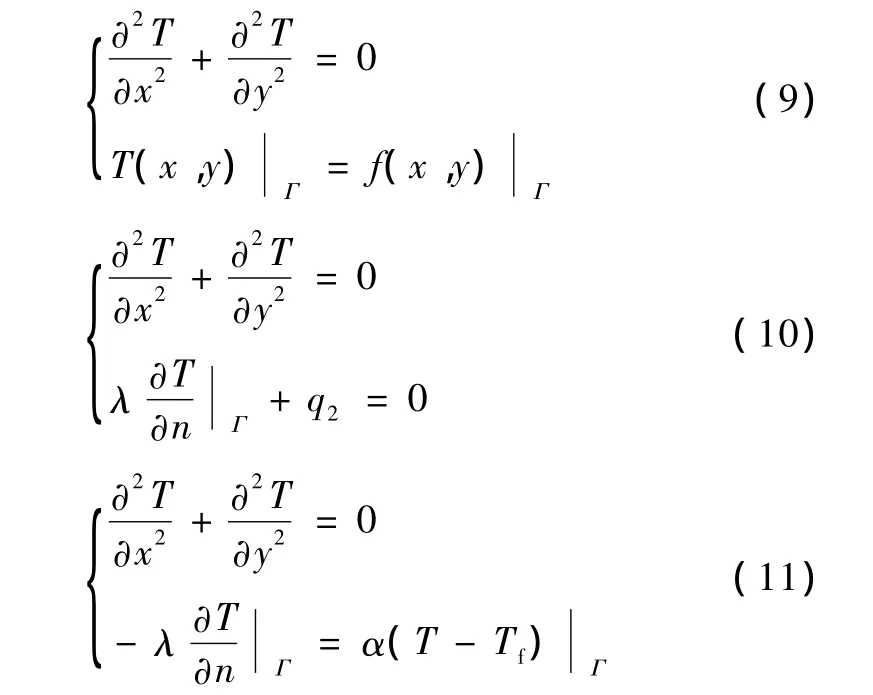
式中，q2为热流密度，W/m2;α为对流换热系数;Tf为流体温度，℃;Γ为积分边界。

有限元计算温度场中常用的计算单元为三角形单元。利用加权余量法和Galerkin法对式(7)～式(11)进行处理，整个区域的有限元方程为

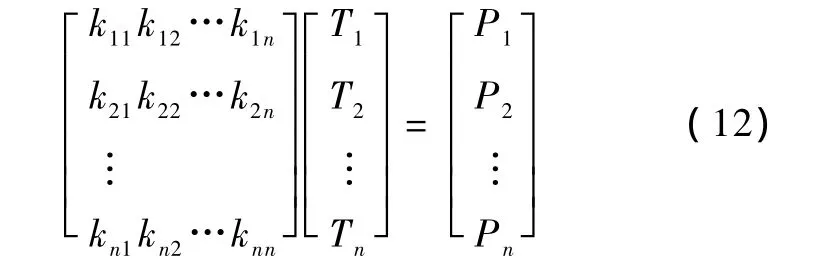
式中，kij、Pi(i=1 ～ n，j=1 ～ n，n是剖分节点数)的计算参见文献［8］。

利用迭代法对方程(2)求解，即可求得各点的温度值。

2 耦合计算

在导体、金属屏蔽层损耗和铠装层损耗计算中，qv为单位时间内，在单位面积上产生的热量，是温度场计算的热源，其数值由式(4)计算而得。而式(4)中的电导率σ是一个与温度密切相关的量，可表示为:

式中，σ20为温度为20℃时的电导率;Tr为导体的温度，℃。

因而，直埋电缆温度场计算是一个温度场与电磁场耦合计算的问题，可由图2所示迭代流程实现。

3 载流量的计算

图2 热电耦合计算流程图Fig.2 Flow chart of thermoelectric coupling

在给定电缆电流后，可根据图2计算流程，利用有限元耦合计算电缆的温度场。对于交联聚乙烯电缆，要求长期工作过程中，导体温度不超过90℃，此时可施加的最大负荷电流即为电缆的额定载流量。载流量的计算可根据图3所示迭代过程计算。

图3 载流量计算流程图Fig.3 Flow chart of ampacity calculation

4 模型仿真

以6/10kV 150mm2YJV22型XLPE电力电缆为例，计算电缆温度场分布。电缆结构参数如表1所示，敷设条件如表2所示。

电缆区域的有限元剖分模型如图4所示。将边界条件离散后，代入温度场的有限元方程，采用交叉迭代法求解，得到整个电缆和周围土壤温度场的分布，整个考虑区域的温度场对称分布;最高温度位于电缆区域，其导体温度值为90℃。温度从电缆到周围土壤温度逐步降低，距离电缆越远，温度越低，最后趋于恒定值，最后降到土壤温度为10℃和地表温度25℃。

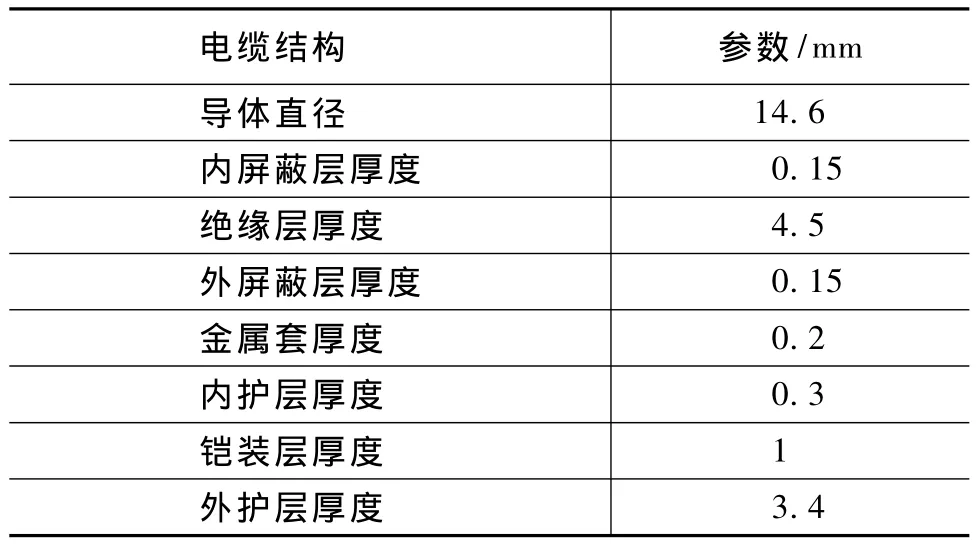
表1 电缆结构参数Tab.1 Parameters of cable structure

表2 电缆敷设条件Tab.2 Installation condition of cable

图4 电缆的有限元剖分模型Fig.4 FEM dissection model of cable

当电缆缆芯温度迭代到90℃时，载流量为362.1A，试验载流量为 365A［9］，误差为 0.8% 。

当不考虑热电耦合时，载流量为375.5A，与试验载流量相比，误差为2.9%。可见，考虑热电耦合时载流量计算结果更接近试验载流量。

当电缆周围回填200mm厚的沙土，且沙土热阻为2.0W·(m2·℃)时，电缆的载流量为319.2A。当三根同型号电缆平行排列敷设，电缆间距为200mm时，电缆的载流量为187A。当电缆周围回填沙土时，三根电缆的载流量为167A。

5 结论

本文以土壤直埋的单根三芯电缆和三根三芯电缆平行排列为例，阐述了采用基于热电耦合的有限单元法对电缆土壤直埋敷设时长时间运行的稳态温度场和载流量计算的方法。在电缆区域和土壤区域的剖分中用到了可变步长的离散化方法，能够在不降低精确度的同时减少节点的数量。

采用数值计算方法确定载流量，可以方便地预测各种载流量时地下电缆的温度值，确保电缆在安全温度范围内工作，对电缆的敷设和运行都有一定的指导意义，应用前景非常广阔。

［1］孔祥谦 (Kong Xiangqian).有限单元法在传热学中的应用(Application of finite element method in calorifics)［M］.北京:科学出版社 (Beijing:Science Press)，1998.

［2］Gela G，Dai J J.Calculation of thermal fields of underground cables using the boundary element method［J］.IEEE Trans.Power Delivery，1988，3(4):1341-1347.

［3］Hanna M A，Chikhani A Y，Salama M A A.Thermal analysis of power cables in multi-layered soil，practical consideration［J］.IEEE Trans.Power Delivery，1993，8(3):772-777.

［4］Hanna M A，Chikhani A Y，Salama M M A.Thermal analysis of power cables in multi-layered soil，part3:case of two cables in a trench［J］.IEEE Trans.Power Delivery，1993，8(3):572-577.

［5］Hanna M A，Chikhani A Y，Salama M M A.Thermal analysis of power cables in multi-layered soil［J］.IEEE Trans.Power Delivery，1993，8(3):761-771.

［6］梁永春，李彦明，柴进爱 (Liang Yongchun，Li Yanming，Chai Jinai).地下电缆群稳态温度场和载流量计算新方法 (A new method to calculate steady-state temperature field and ampacity of underground cable system)［J］.电工技术学报 (Trans.China Electrotechnical Society)，2007，22(8):185-190.

［7］梁永春，孟凡凤，王正刚 (Liang Yongchun，Meng Fanfeng，Wang Zhenggang).电缆群邻近效应的计算和优化排列 (Proximity effect and optimized arrangement of cable bundles)［J］.电工电能新技术 (Adv.Tech.of Elec.Eng.＆ Energy)，2006，25(2):39-41.

［8］梁永春，柴进爱，李彦明 (Liang Yongchun，Chai Jinai，Li Yanming).有限元法计算交联电缆涡流损耗 (Calculation of eddy current losses in XLPE cables by FEM)［J］.高电压技术 (High Voltage Eng.)，2007，33(9):196-199.

［9］马国栋 (Ma Guodong).电线电缆载流量(Ampacity of wire and cable)［M］.北京:中国电力出版社 (Beijing:China Elec.Power Press)，2003.5-29.