热电发电装置的动态模型及分析

袁义生，熊 晶

(华东交通大学电气学院，江西 南昌330013)

1 引言

能源紧张及环境污染的加剧使得废热回收技术成为提高能源利用率的一个重要研究方向。以汽车为例，传统汽车石油燃料产生的能量约30%转换成机械能来驱动汽车行驶，另外约40%以废气方式排放，还有约30%在引擎冷却过程中流失，其能源利用率极低［1-2］。因此，研究如何将这些废热回收利用是一项极其有益的研究工作。

热电发电装置由热端导热片、热电发电器件和冷端散热片构成，之后再经后级直流变换器将热电发电器件发出的电能转换后送给蓄电池储存。

但热电发电及变流装置要得到广泛应用，还有一些基础性问题需要解决，其中重要一点就是热电发电装置的数学模型的建立。这是因为后级直流变流器的控制特性，包括做最大功率跟踪和功率匹配［3］时的动态特性都与前级热电发电装置的动静态模型密切相关。然而，现有的热电发电器件的模型有两种，一种是设计模型，另外一种是电等效模型。设计模型是基于器件物理特性而建立的微观参数模型，主要为评估器件Seebeck效应建立，此类模型主要是不考虑器件工作条件的物理静态模型［4］，也有少数考虑了外部工作条件的准动态模型［5］。电等效模型则是将热电发电器件的输出等效为电压源U和内阻Rin串联电路。此类模型可以由厂家给出特性参数。但问题是，器件厂家标示的器件参数是在器件两端温差ΔT和负载固定的静态条件下测量得到的，并不反映热电发电器件的动态特性，尤其是大信号特性。而且，热电发电器件处于热端尾气管和冷端散热器之间，这两者的特性对热电器件的输出电压动态特性都有影响;还有就是后级直流变换器的等效输入电阻对热电发电器件的输出电压也有影响。这些都是之前的研究没有系统考虑的问题。

所以，本文建立热端导热片、热电发电器件和冷端散热器构成的完整热电发电装置的动态模型。分析热电发电器件输出电压的热源响应特性，以及输出负载响应特性。建立等效仿真电路模型，并用小装置试验测试验证了模型的正确性。

2 热电发电装置结构及原理

热电发电装置由热端导热片(散热片)、热电发电器件和冷端散热器构成，如图1所示。其中，因为热电发电器件为双层半导体串联结构，表面不绝缘，所以在热冷端散热器与热电发电器件之间还有绝缘陶瓷片。而虚线框的后级直流变换器部分可用一个等效负载电阻Ro来代替。

图1 热电发电装置结构Fig.1 Structure of thermoelectric generator equipment

热电发电器件Seebeck效应的输出电压表示为:

式中，α是 Seebeck系数;ΔT是热电发电器件热端和冷端间的温差。α值由材料特性决定。但ΔT却不仅取决于热电发电器件的传热特性，由图1可知也与热源变化、冷热端散热片传热特性和等效负载电阻Ro有关。所以，建立完整的热电发电装置模型需要逐个建立上述部件数学模型并连接构成。

3 散热片动态模型

对任意微小封闭容积，据热力学第一定律［8］有:

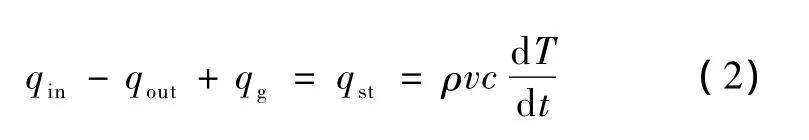
式中，ρ、v、c分别为此封闭容积的密度、体积、比热容;q表示能量流动的速率，即热流量。此式表示控制容积中的能量速率的增大，必定等于进入控制容积的能量速率，减去离开控制容积的能量速率，再加上在同一瞬间控制容积内产生热量的速率。

由于导热系数恒定，温度沿厚度方向线性分布。如果散热片很薄，可以使用两端平均温度代替散热片温度。定义其两端温度分别为T1和T2，则有:

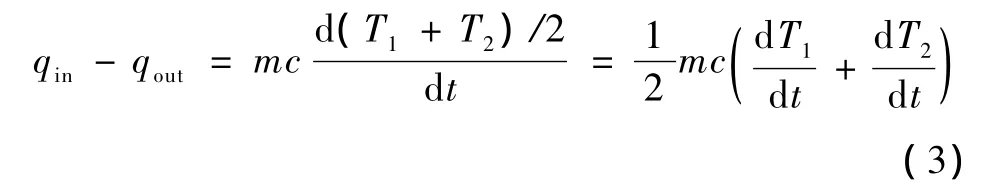
式中，m为封闭容积的质量。再结合基本的静态热阻定律:

式中，θ表示散热片的热阻。可以得到热冷端散热器完整的静动态特性等效电路如图2所示。

4 热电发电器件的动态等效模型

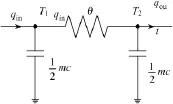
图2 平板散热器等效电路图Fig.2 Equivalent model of flat heatsink

为了提高热电转换效率，热电发电器件通常制作成平板状。当热电发电器件输出接负载电阻Ro时，体内的热能就转换成电能，有:

式中，Rm是热电发电器件本身电阻。

对于半导体热电模块，考虑塞贝克效应及帕尔帖效应，单位时间内从热接触层吸收的热量为:

热电器件单位时间内放给冷端接触层的热量为［9］:

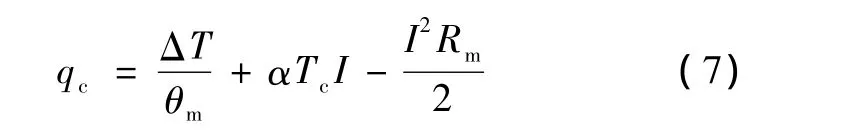
式中，Ta和Tc分别为热电模块热面和冷面的温度;θm为热电模块的热阻。并且:

根据热力学第一定律可得:

可以建立热电模块的等效模型，如图3所示。

图3 热电发电器件等效模型Fig.3 Equivalent model of thermoelectric generator

5 完整模型及分析

5.1 完整模型

在上述分析的基础上，据图1装置结构可以得到完整的热电发电装置的等效电路模型如图4所示。

图4 热电发电装置等效电路模型Fig.4 Equivalent circuit model of thermoelectric equipment

在图4中，T1、T2分别为热端和冷端温度;θ1为热端散热片的热阻;C1为热端散热片的热容，其值为热端散热片的质量与比热容的乘积的1/2;C3为热电发电器件的热容;θ4为冷端散热片的总热阻;C2为冷端散热片的热容;θ2和 θ3分别为热端和冷端导热陶瓷垫片热阻和接触热阻之和;Rm和Ro分别为热电发电器件的内阻和等效负载电阻。因为绝缘陶瓷片热容小，因此图中忽略。

5.2 模型分析

(1)源响应

源响应是指热源波动对Seebeck输出电压的影响。假定热源信号阶跃变化，而热电发电器件输出开路，即在图4中设定I=0，Ro断开，就可以分析模型的源响应特性。这是一个多阶的热阻容θC惯性电路。热电发电器件Seebeck效应输出电压U与ΔT(Ta－Tc)成正比。当 qin是一个初始为零的阶跃函数时，ΔT的稳态值就等于qinθm，但其暂态分量则取决于各串联的热阻容乘积。在实际的系统中，热端散热片热容大;热电发电器件的热容则最小;冷端散热片的热容较大。所以，ΔT的暂态分量主要取决于θ1C1和θ4C2两个时间常数。即 Seebeck效应输出电压U的源阶跃响应特性曲线是一个简化的二阶惯性环节。

(2)负载响应

负载响应是指等效负载电阻Ro(后级直流变换器电路等效输入电阻)阶跃变化时，Seebeck效应输出电压U的响应特性。此时可以假定热源稳定。等效电路如图5所示。

分析负载由开路(R=∞)阶跃变化至 Ro时的输出电压响应。由于Ro和Rm的分压，此时负载电压Uo会瞬间降低。之后，因为IU/2的分流作用，流过 θm的热量 qm下降;且(αTa－IRm/2)Iθm的存在，使得热冷端温差ΔT下降。所以，负载电压Uo会继续随Seebeck电压U下降而下降。由于热电发电器件的效率很低，IU/2远小于qa，所以负载电压Uo继续下降的过程中可以忽略热端散热器的影响qa不变。此时，负载电压Uo基本按θmC3时间常数规律下降至稳定值。

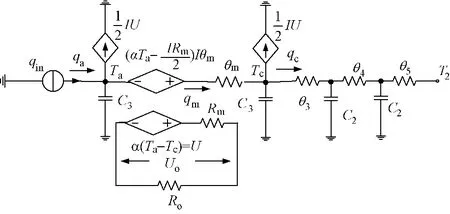
图5 负载响应等效电路Fig.5 Equivalent circuit of load response

综上所述，可以看出:热电发电装置输出电压的变化在其物理特性基础上，不仅与热源的改变，也与后级负载的变化有关。

6 仿真与实验

在实验室搭建了一个小型热电发电装置，其中的热电发电器件采用了一片Hi-Z公司生产的HZ-14(可见该公司网站)，热源采用热风枪来模拟，冷端采用强迫风冷使冷端散热器外侧温度与空气温度接近。

按照图4在电路仿真软件SABER中建立仿真电路模型。其中的温度，热阻和热容分别用电压，电阻和电容来代替。

系统各部分的热阻和热容按照文献［8］中公式计算，热电发电器件的热阻在说明书中查。参数见表1。

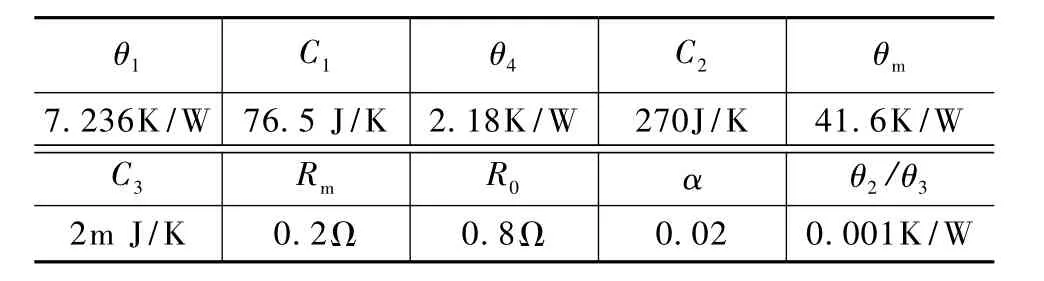
表1 仿真和试验参数Tab.1 Parameters of simulation and experiment

实验首先测试了装置的负载响应特性。在热源及温度稳定的条件下，投卸等效输出电阻 Ro，测试其输出电压响应特性。其中，图6(a)和6(b)分别为投载下仿真和实验的负载电压Uo波形图。图7(a)和7(b)分别为卸载下仿真和实验的负载电压Uo波形图。由图可见，投载瞬间负载电压Uo先迅速下降，而后沿曲线下降约5s后稳定。卸载时相反。实验和仿真结果吻合。

图6 投载下Uo仿真和实验波形Fig.6 Simulation and experimental waveforms ofvoltage Uoin load-on transient

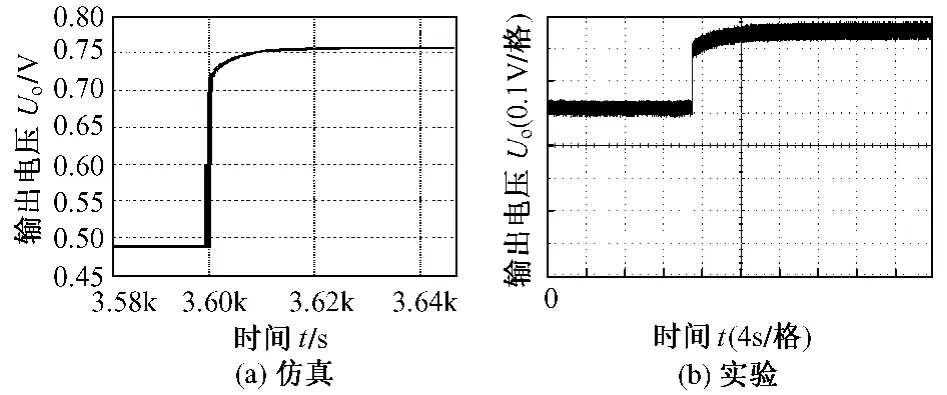
图7 卸载下Uo仿真和实验波形Fig.7 Simulation and experimental waveforms of voltage Uoin load-off transient

其次测试了装置的源响应特性。在热源加热温度稳定后断开热源，分别考察空载和带载情况下的负载电压Uo响应。图8(a)和8(b)分别是空载下仿真和实验波形。图9(a)和9(b)分别是带载下仿真和实验波形。可见，源响应负载电压Uo下降时间达到1800s，远远超过负载响应时间，这与第4节的分析吻合。另外，带载下的源响应速度略快于空载下的源响应速度，但并不显著，这是因为热电发电器件的效率低，输出电功率远小于传递的热量。

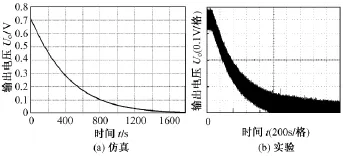
图8 空载下断热源时Uo仿真和实验波形Fig.8 Simulation and experimental waveform of voltage Uoin hot source cut-off transient without load

图9 带载下断热源时Uo仿真和实验波形Fig.9 Simulation and experimental waveform of voltage Uoin hot source cut-off transient with load

7 结论

建立了热电发电装置的动态模型和等效电路模型，分析了其源响应和负载响应特性。指出了热电发电器件的输出电压源响应是一个由散热器决定的大时间惯性特性曲线，而负载响应则是由热电发电器件决定的小时间惯性特性曲线。这对后级直流变换器主电路和控制电路的进一步研究具有重要参考价值。建立的小型实验装置的实验和仿真结果吻合，证明了模型的有效性。

［1］Yang Jihui.Potential applications of thermoelectric waste heat recovery in the automotive industry［A］.2005 International Conference on Thermoelectronics［C］.New York，USA，Aug.2005.19-23.

［2］Yang Jihui.Development of thermoelectric technology for automotive waste heat recovery［R］.Washington:DOE USA，2008.

［3］Rae Young Kim，Jih-Sheng Lai.A seamless mode transfer maximum power point tracking controller for thermoelectric generator applications［J］.IEEE Trans.on Power Electronics，2008，23(5):2310-2317.

［4］宋瑞银，李伟，杨灿军，等 (Song Ruiyin，Li Wei，Yang Canjun，et al.).微小型热电发电器建模及优化设计研究(Modeling and optimal design for mic-thermoelectric generator)［J］.太阳能学报 (Acta Energiae Solaris Sinica)，2006，27(6):554-558.

［5］Rasit Ahiske.New method for investigation of dynamic parameters of thermoelectric modules［J］.Electric Engin，2007，15(1):51-65.

［6］Simon Lineykin，Sam Ben-Yaakov.Modeling and analysis of thermoelectric modules［A］.IEEE APEC 2005［C］.New York，USA，2005.2019-2023.

［7］Chavez J，Ortega J，Salazar J，et al.Spice model of thermoelectric elements including thermal effects［A］.Proc.Instrumentation and Measurement Tech.Conference［C］.New York，USA，2000.1019-1023.

［8］Incropera F P，葛新石译 (translated by Ge Xinshi).传热和传质基本原理 (Fundamentals of heat and mass transfer)［M］.北京:化学工业出版社 (Beijing:Chemical and Industry Press)，2009.

［9］Omer S A，Infield D G.Design optimization of thermoelectric devices for solar power generation［J］.Solar Energy Materials and Solar Cells，1998，(53):67-82.