基于根轨迹法的随动系统PID 控制

邵中年，张志瑞

(海军驻包头军事代表室，内蒙古 包头 014030)

随动系统(伺服系统)输入信号是变化规律未知的任意时间函数，要求被控变量按同样规律变化并与输入信号的误差保持在规定范围内。对随动系统而言，被控制量始终跟踪参考量的变化［1］。快速性、精确性和平稳性是现代战争对舰炮随动系统的基本要求。虽然系统本身的反馈装置可以较好地满足系统的跟踪精度和快速性的要求，但是由于系统中存在的非线性因素甚至是不确定因素，为了实现更好的系统性能，除了提高一些装置自身的精度外，重要的是还需采用先进的控制策略。

由于具有结构简单、调整容易、控制效果良好等优点，PID 控制已在工业控制中得到广泛应用［2］。但是，随着被控对象的机理日益复杂，非线性、慢时变、纯滞后、参数与结构的不确定性等导致传统的PID 控制很难再得到理想的效果。多年来，为了克服传统PID 控制的不足，提高其鲁棒性，人们提出了许多新的控制算法，如参数自调整PID 控制、模糊自适应PID 控制［3-7］等。S 平面上的根轨迹可以用图解法来确定，当一个参数变化时，根的变化轨迹即为根轨迹图。根轨迹法是分析设计反馈控制系统的有效工具。本文将采用依据根轨迹法设计的PID 控制来实现对舰炮随动系统的控制。

1 舰炮随动系统及其数学模型

随动系统的任务是控制机械负载的位置，使其与参考位置相协调。典型随动系统结构如图1 所示。而舰炮瞄准随动系统是使舰炮作旋回和俯仰等运动的装置总称，其任务是根据火控信息，带动舰炮及时、准确地跟踪、瞄准目标［1］。舰炮随动系统一般采用复合控制，主要是电流反馈、速度反馈和机械反馈3 个负反馈以及前馈装置，其工作原理见图2。

图1 随动系统总体结构

图2 舰炮随动系统原理

对于本文所研究的舰炮随动系统(交流伺服系统)来说，可以认为伺服放大器和交流伺服电机综合起来，构成一个速度环。这个速度环可以近似为一个一阶惯性环节:

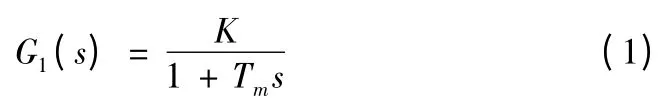
其中:Tm是系统的电气时间常数;K 是系统的开环放大倍数。从速度环到系统的输出控制量之间是一个积分环节:

于是整个伺服系统的开环传递函数为

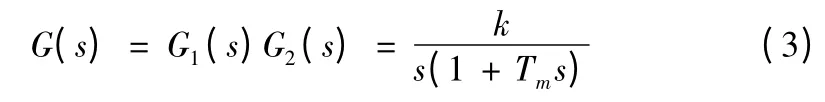
从上面的结果可以看出，只要测出k 和Tm的值，就能够得到速度环的模型，并进而得到整个伺服系统的传递函数模型。

在实际的测量当中，给定系统一个阶跃信号，通过严格的时间间隔来测出交流伺服电机转轴的角位置，并记录下来，经过差分、滤波计算后，求出电机的时间常数和转速值。与此同时，也可以用转速表测量出伺服电机的转速值。

综合实验测得的数据，可以得到Tm=0.162 s，k =416 mil/s v。因此，伺服系统的传递函数(数学模型)如下:

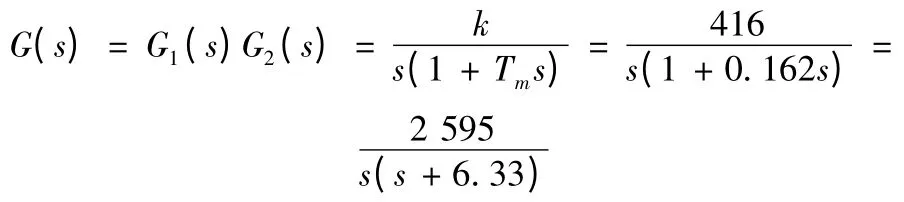
需要说明的是，在工作过程中，被控对象的模型是变化的，这里可以用近似的传递函数来表征伺服系统在无转动惯量、无冲击和力矩干扰等情况下的系统动态特性，并以此传递函数作为设计系统控制器以及系统仿真的基础。

2 舰炮随动系统PID 控制器的设计

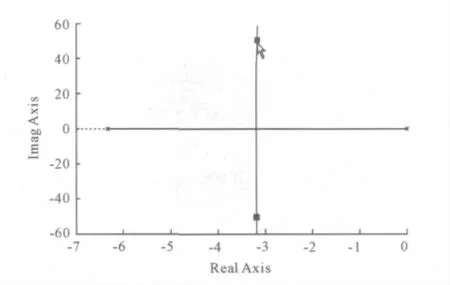
图3 前向传递函数为G(s)且为单位反馈时系统根轨迹

由图3 可知该系统的闭环极点位于s = -3.165 ±j50.8，阻尼比ζ 为0.062 1。无阻尼自然频率ωn为50.9，静态速度误差常数kv为410 s-1。由于其阻尼比很小，系统响应会出现剧烈振荡［8］，所以，必须适当调大ζ。现在假设需要使主导极点的阻尼比等于0.5，ωn不变，静态速度误差常数kv增加到4 100 s-1，为原kv的10 倍。设计一个适当的校正装置，以满足所有的性能指标。该校正系统将具有下列传递函数:

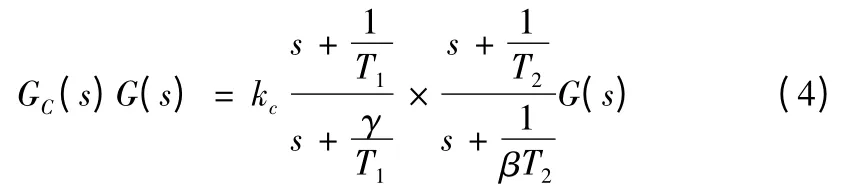
其中γ≠β。根据性能指标，主导闭环极点必须位于-25.45 ±j44.08。

为了设计校正装置的相位超前部分，首先需要确定产生53°辐角增量的零极点的位置。这里有很多种选择，但本文选择零点位于s= -6.33，以便使零点与被控对象的极点s = -6.33 相抵消。零点选定之后，相应的极点位置便可以确定。为保证辐角增量为53°，必需满足通过图解分析及简单计算，可知极点必须位于s= -49.991。

根 据 辐 值 条 件 确 定 kc的 值:

校正装置的相位滞后部分设计如下:首先根据对静态速度误差常数的要求确定β 的值4 100，因此确定β=79.814 2。

最 后， 选 择 T2值 足 够 大， 使 得 - 5° ＜基本满足上述两项条件，因此可选择T2=5。

于是，可得设计出来的PID 控制器传递函数为

此时，已校正系统将具有下面开环传递函数:Gc(s)G(s)

3 仿真结果分析

图4 系统对25t 度位置斜坡响应误差曲线

仿真结果表明，系统静态误差小于0.5 mil，等速跟踪误差小于1 mil，正弦跟踪误差小于1 mil，在系统的结构参数k 和Tm发生较大变化时，该PID 控制器具有很好的自适应性和鲁棒性，即使输入响应信号特性发生大范围变化，系统仍能很好地跟踪输入信号，具有很好的控制性能。

4 结束语

为了能够实现对目标的精确跟踪和打击，需要舰炮随动系统具有高精度、高快速性。本文利用根轨迹法建立PID 控制器，基本保留了常规PID 控制器的优点，结构简单、易于控制;同时利用根轨迹法对控制参数进行校正，使得整个系统具有良好的鲁棒性和自适应性，将其加入到随动系统的控制中，并进行仿真。结果表明，采用根轨迹法PID控制能够使随动系统性能的更加符合战术技术要求。

［1］田福庆，刘云秋，周耕书，等.舰炮随动系统设计原理［M］.武汉:海军工程大学，1997.

［2］曾军，方厚辉.神经网络PID 控制及其Matlab 仿真［J］.现代电子技术，2004(169):51-52.

［3］Chang W D，Hwang R C，Hsieh J G.A self-tuning PID control for a class of nonlinear systems based on the Lyapunov approach［J］.Journal of Process Control，2002，12(2):233-242.

［4］Carvajal J，Chen G，Ogmen H.Fuzzy PID controller:Design，evaluation，and stability analysis［J］.Information Science，2000，123(3/4):249-270.

［5］胡浩，黄文玲.压力仿真系统模糊自适应PID 控制［J］.四川兵工学报，2010(7):112-114.

［6］卢海洋，林平.基于模糊PID 控制的UUV 定深控制系统设计［J］.重庆理工大学学报:自然科学版，2011(6):58-62.

［7］栾军山，陈华.Smith-模糊PID 在过程控制中的应用［J］.重庆理工大学学报:自然科学版，2010(7):106-109.

［8］胡寿松.自动控制原理［M］.北京:科学出版社，2002.