导弹对空中目标毁伤的坐标系转换方法及应用

张云昆，张 龙

(南京理工大学 机械工程学院，南京 210094)

1 三个坐标系

1.1 目标坐标系

目标坐标系(oxtytzt)，坐标原点为目标的几何中心，oxt轴沿目标质心速度方向，向前为正;oyt轴位于铅直平面内，向上为正;ozt与oxt、oyt构成右手系，向右为正。如图1 所示。

图1 目标坐标系示意图

1.2 导弹几何坐标系

导弹几何坐标系(oxmymzm)，坐标原点为导弹质心，oxm轴沿导弹速度方向，向前为正;oym轴位于铅直平面内，向上为正;ozm与oxm、oym轴构成右手系，向右为正。如图2 所示。

图2 弹体坐标系示意图

1.3 相对速度坐标系

相对速度坐标系包含目联相对速度坐标系和弹联相对速度坐标系。

目联相对速度坐标系(oxyz)，坐标原点为目标的几何中心，ox 轴与相对速度矢量平行;oy 轴位于垂直平面内，向上为正;oz 轴与ox、oy 轴构成右手系，向右为正。

弹联相对速度坐标系(oxryrzr)，坐标原点为导弹的炸点，各轴与oxyz 各轴平行。

目联相对速度坐标系(oxyz)和弹联相对速度坐标系(oxryrzr)如图3 所示。

图3 相对坐标系及弹目之间姿态关系

2 坐标系间转换

2.1 目标几何坐标系和目联相对速度坐标系转换

如图4 所示，当给出攻击平面相对目标翼面的倾角αH和在攻击平面的截获角χ 或航向角q 时，

其中，转换矩阵

式中:(x，y，z)为oxyz 坐标系中的点坐标;( xt，yt，zt )为oxtytzt坐标系中的点坐标。

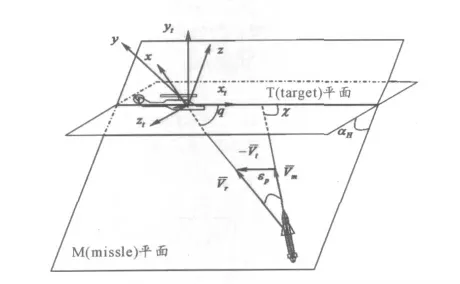
图4 弹、目平面关系

2.2 导弹几何坐标系和弹联相对速度坐标系转换

式中，转换矩阵

其中:δm为导弹攻角;βm为导弹侧滑角;εp为导弹前置角。

当δm≠0，βm=0 时，则

当δm=βm=0 时，oy 轴与oyr轴重合，则

式中

其中:Vt为目标速度;Vm为导弹速度;Vr为相对速度。

3 坐标系转换应用

在求导弹破片流相对速度时，涉及到速度方程从弹体几何坐标系到弹联相对速度坐标系的转换。

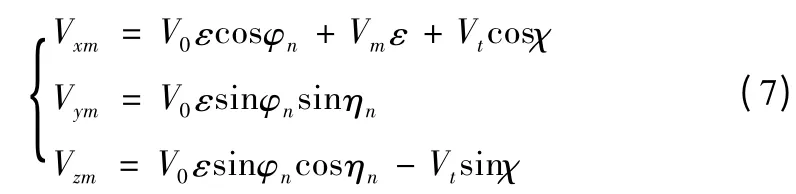
描述导弹破片流的运动，若攻角δm=0，其在弹体几何坐标系中的相对速度方程为式中:V0为战斗部静爆时破片初速;φn为在经过战斗部纵轴平面内破片的平均飞散方向角;ηn为在赤道面内破片的平均飞散角度;χ 为攻击平面内相对于目标oxtzt面内的截获角。

为便于分析，通常用导弹的相对速度向量Vr描述比较方便，于是将导弹几何坐标系(oxmymzm)转换为弹联相对速度坐标系(oxryrzr)，则式(7)转换为

4 结束语

排除直接命中目标，导弹破片流对目标的毁伤取决于落在目标上的破片数ΔN、遭遇速度VB和破片流的进入角δ0。如果给出确定破片流在相对运动中的导弹接近目标的条件Vm、Vt、δm、χ(或q)、αH和H 以及战斗部相对目标炸点的坐标 (x，y，z)，通过坐标系变换等方法，则可以求出上述3 个参数。

［1］蔡满意.飞行控制系统［M］.北京:国防工业出版社，2007.

［2］李新国，方群.有翼导弹飞行动力学［M］.西安:西北工业大学出版社，2004.

［3］王凤英，刘天生.毁伤理论与技术［M］.北京:北京理工大学出版社，2009.

［4］郑振忠.装甲装备战斗毁伤学概论［M］.北京:兵器工业出版社，2004.

［5］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2006.

［6］杨绍卿.火箭外弹道偏差与修正理论［M］.北京:国防工业出版社，2011.