基于蒙特卡洛模拟的地铁对公交线网布局影响分析

周 媛

(西安外事学院工学院汽车运用系，陕西西安 710077)

0 引言

随着经济和社会的发展，城市化水平的提高，城镇和农村人口向城市聚集，城市规模越来越大、人口越来越多，使得乘车需求激增，传统的以公交车为主体的公共交通模式已经无法满足市民的乘车需要。为了缓解当前公共交通面临的巨大压力，地铁轨道交通凭借其容量大、速度快的特点，逐渐成为城市公共交通的重要组成部分，因此城市公共交通系统如何应对这种新的变化亟需研究，本文以西安为例对此进行了探讨。

目前西安城市公共交通已具有一定规模，并且为西安社会经济的建设与发展做出了贡献，但仍存在一些问题，比如公共交通出行时间过长，降低了吸引力;公交线网布局不合理;公交线网密度整体水平偏低;公交优先政策和管理措施不强等，影响着公共交通系统优势的发挥［1］。为了能够缓解上述存在的问题，西安市政府开展了城市地铁的规划和修建工作，然而现有公交线路已存在多年，建设地铁线路必然会对已有公交线路产生影响。地铁的铺设会导致地铁线路辐射范围内的公交线路的调整，例如将与地铁线路重合部分的公交线路撤销或减少班次，适当增加便于换乘地铁的公交线路等。因此平衡公交车与地铁的客流分配，使公共交通系统的效益最大化便是现存的一个主要问题。显然，这类问题属于交通规划中的交通网络均衡配流问题。在过去的30 a中交通网络均衡配流问题取得了不少的研究成果，但是关于公共交通网络均衡配流的相关成果却较少［2］。目前最常用的做法便是采用 wardrop第一、第二均衡准则来完成配流，但是这种传统方法要求公共交通系统的主要参数是确定的。这一假设往往并不与实际情况相符，从而导致了该模型得到的结果与实际情况偏差很大［3］。

为了能够精确预测地铁投入使用后给人们的乘车带来的方便程度，以及对现有公交路线的影响，本文首先根据西安市当前公交汽车系统数据，以“平均候车时间最短”和“平均换乘次数最少”这两项市民出行最常考虑因素为目标函数［4，5］，优化得出任意两个公交汽车站点之间的最优路线，并通过计算机模拟仿真得到在没有修建地铁时公交系统的平均客流量和乘客平均候车时间。然后，在同样的代价函数下，结合地铁的相关数据，优化得到任意两个站点之间的最优线路，以及此时公共交通系统的效率指标。以此比较说明地铁对公交系统效率的提高。这种做法可以摆脱传统算法对参数确定性的要求，更多的融入一些实际因素，使得预测结果更加接近实际情况。进而在此基础上，通过比较地铁修建前后周边公交线路的客流量和乘客平均候车时间的改变情况给出铺设地铁后，公交车系统运营线路规划的改进意见。

1 对公共交通系统的评价模型

公共交通系统是一种为了最大程度方便市民出行的公共服务系统。故本文重点从乘客的角度出发，选取平均乘车时间和路段客流量作为定量评价公共交通系统主要指标。

1.1 平均候车时间

通常，衡量一个城市公共交通系统是否有效，最主要的一个判断准则就是市民在该系统中的平均候车时间。平均候车时间越短，说明该公共交通系统越有效。反之，则说明该系统的效率越低。因此，平均候车时间是本文选择描述公共交通系统的一个重要指标。

1.2 路段客流量

城市公共交通系统的客流拥挤程度也是反映该系统运行效率的一个因素。如果一个城市的市民总是面对十分拥挤的乘车状况，则说明该系统不能满足目前该市市民对公共交通系统的服务需求。反之，则说明该系统运行效率能够满足需求。因此，路段客流量也是本文选择的一个描述公共交通系统的指标。

上述两个指标，在下文中统称为公共交通系统的效率指标。

为计算公共交通系统的效率指标，本文采用计算机模拟的方法来获得统计意义下的效率指标。首先选取地铁路线附近的公交路线作为研究对象，依据蒙特卡洛模型随机生成各个行人的出行起点及终点。假设每个人按照乘车的“最佳路线”情况下进行出行路线选择，进而统计出所有乘车路线上的平均客流量和乘客平均候车时间。其流程图见图1。

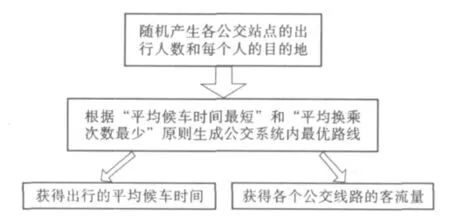
图1 公交系统中乘客平均候车时间和平均客流量计算流程图

然而“最佳路线”在每个人的心中都是不同的，很显然仿真模型中的路线选择与现实生活越接近，模型得到的数字结果就越具有说服力。因此，我们从实际情况出发，对市民出行乘坐公共交通的心理做了调查［5］，得到乘客对公交系统的需求期望分布，如图2所示。

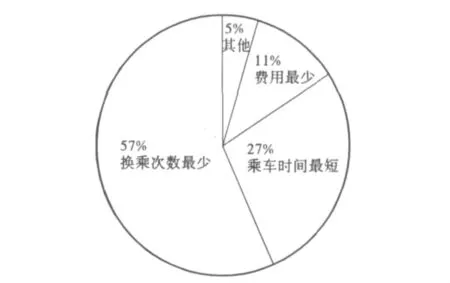
图2 乘客对公交系统的期望分布图

由图2可以看出，市民在选择公交路线时，有56.7%优先考虑换乘次数，27%优先考虑行程时间。市民对公交路线的选择往往是通过对上述这两个因素进行综合而得到的。因此，我们在考虑市民乘车路线选择时应着重考虑“换乘次数”和“行程时间”这两个指标。以图G(V，E)来表示一个城市的公共交通网络，其中V代表该城市公共交通网络的所有站点的集合，E表示该市公共交通网络的所有道路的集合。假设某市民的乘车起点为k，终点为l，xkl表示一条起点为k，终点为l的通路。此时路线选择的优化模型如式(1)所示:

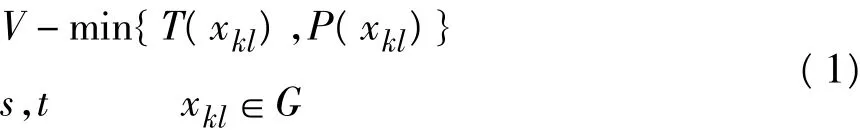
模型中T(xkl)表示路线xkl所需要的行程时间，P(xkl)表示路线xkl所需要的换成次数。

由式(1)可以看出，市民的出行选择是个多目标优化问题。本文采取运筹学中目标规划的策略来获取上述多目标优化问题的近似解。即把2个优化目标中的1个变为目标约束，通过给定目标约束的取值范围，将多目标优化问题转变成了一个单目标优化问题［6］。此时式(1)转化为:

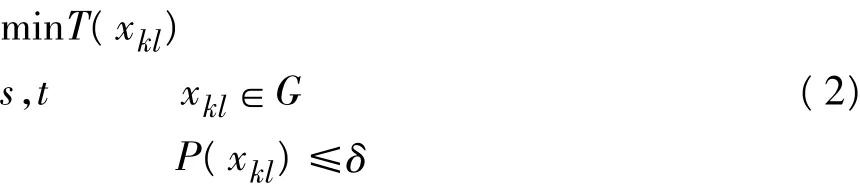
其中δ表示公民出行时可以容忍的最大换乘次数。

从上述优化模型可以看出，通过将换乘次数这一目标函数转化为优化模型的约束条件，式(1)所示的多目标优化问题已经转化为一个单目标优化问题。下面给出式(2)所示的优化模型的求解方法。

首先生成各个站点间的邻接矩阵X。其中Xij存放在公交站点i与公交站点j之间的连接情况。如果这两站点是存在交通工具将其相连的，那么Xij中的值为从站点i到站点j之间的乘车时间，否则其中的值为－1。通过公交站点与路线的信息存入邻接矩阵，便可以利用矩阵中各个相邻站点间的距离信息得出在已知乘车路线起点和终点的情况下的距离最短路线。接下来对换乘次数最大值进行限制(本文在进行数据处理时δ取值为2)，并且对上述最短路线所需要的换乘次数与换乘次数最大值进行比较。如果该最短路线所需的换乘次数小于最大限制，便认为公民在乘车时会选择该路线，否则将选择另外一条距离次短的路线进行判断。具体操作流程如图3所示。

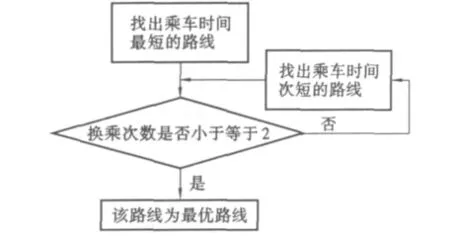
图3 公交车最优路线寻找方法

2 评价指标的求解及公交系统线路改进建议

本节将通过上述评价模型来预测西安市地铁修建好后会对公交系统效率指标的影响［7］。

Step1:生成10 000个自然数用来代表乘车的10 000个人，分别给他们编号1至10 000，并同时随机给出各个乘客的出现时间;

Step2:随机生成每个人的乘车路线的起点与终点;

Step3:应用上节中找最优乘车路线的求解算法，找出每个人乘车的最佳路线选择;

Step4:统计Step3中所有的乘车路线，得到每条路线(地铁路线和公交路线)的客流量。

计算结果见表1。

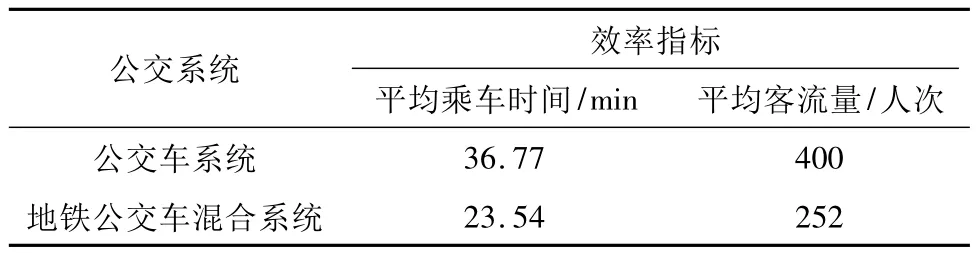
表1 公交系统效率指标

以102路公交车劳动路—玉祥门路段为例，1 d当中的各个时段的平均客流量示意图如图4所示［8］。从图4－a可以看到，在每天8点，12点与18点、21点，是此路段公交运输的高峰期，公交系统压力较大。

地铁开通后，仍以102路公交车劳动路—玉祥门路段为例，1 d当中的各个时段的平均客流量示意图如图4－b所示。根据示意图可以看到，在每天8点，12点与18点、21点，此路段公交运输的高峰期的公交系统压力，相较没有地铁之前降低，且在高峰时段与非高峰时段的客流量差异也降低了。

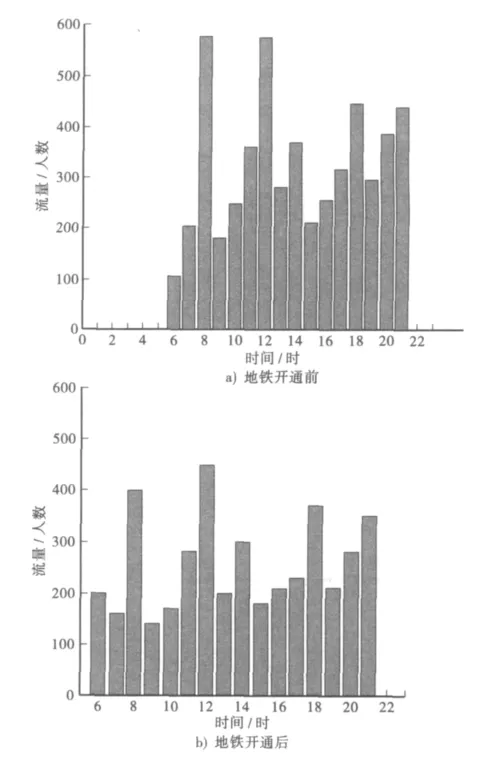
图4 地铁开通前后公交路线平均客流量

从西安市地铁建设图(图5)中可以看到，红色椭圆圈内黑色线路即为102路车与地铁线路重合线路，导致原先这条公交线路上的客流量分流给地铁线路。

所以，地铁投入使用后，在客流量高峰时段，公共汽车线路的客流量平均下降了23.4%。当然，此条线路公交汽车线路与地铁线路重合部分较多，所以较多的分担了公交系统的客流量，在其他线路上，地铁的分流量将可能小于此数值。

由此可见，地铁线路的投入使用，必然会对市民出行时交通工具及交通路线的选择产生很大的影响。一方面地铁为市民出行提供了很大的便利;另一方面使某些已有公交路线客流量大大减少。对于这样的公交路线，政府有必要做出相应的调整，这样既可以节省政府开销，又能够缓解交通拥堵。笔者建议根据客流量变化情况进行线路调整。

1)对承担客流量比例很小的路线建议撤销。该线路乘客的乘车需求可由其他路线满足。

2)对于承担客流量较少的路线，建议按比例减少这些线路的公交车班次，有利于充分发挥每辆公交车的运载能力。

3)对仍承担客流量比例较高的公交路线应当保留。

根据上述路线调整建议，102路公交线路的调整方案如下:

102路公交车的路线为公园南路北口－互助路立交－兴庆路－兴庆公园北门－鸡市拐－东门－大差市－民乐园－五路口－革命公园－北新街－北大街－莲湖公园－红湖街－洒金桥－玉祥门－潘家村－劳动路。其中，兴庆路、东门、大差市、五路口、北大街、洒金桥、玉祥门、劳动路这几个公交站点与地铁站点重复，其重复率为45%，如图5所示。按照上述线路调整方案应将公园南路北口至五路口之间的公交路线关闭，即将互助路立交、兴庆公园北门、鸡市拐、民乐园几个站点撤销，同时将五路口至劳动路的公交线路相应减少。

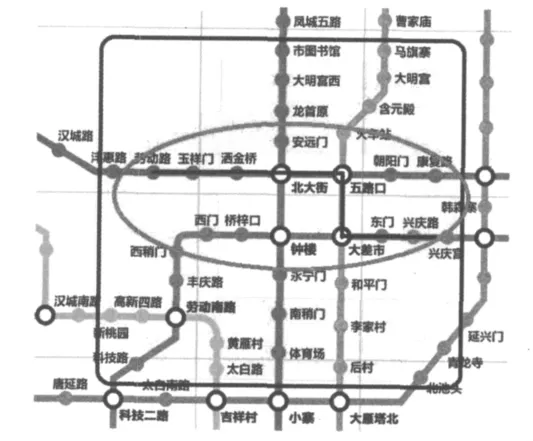
图5 西安市地铁建设图［8］

3 结论

本文针对实际生活中的公交路线选择问题，首先分析了影响乘客选择乘车线路的主要因素，然后调查了西安公交线路、地铁线路的铺设与运营情况。根据此调查数据，在“平均乘车时间最短”和“平均换乘次数最少”的原则下，分别计算出地铁投入使用前后公交系统中任意两个站点之间的最佳乘车路线。最后，通过统计模拟市民的乘车需求，在地铁、汽车混合的公交系统中分别计算得到各个站点的客流量，分析了两个系统中客流量分布的改变情况，提出汽车公交系统运营线路规划的改进意见。

［1］王玉萍，马超群.公共交通特性分析与发展对策研究［J］.西安建筑科技大学学报，2006(6):846－850.

［2］四兵锋，高自友.城市公交网络均衡配流模型及算法的研究［J］.公路交通科，1998(3):41－44.

［3］牛学勤，王 炜.基于最短路搜索的多路径公交客流分配模型研究［J］.东南大学学报，2002(6):917 －919.

［4］谭泽光，姜启源.公交车调度问题的数学模型［J］.工程数学学报，2002(2).

［5］王 炜，杨新苗，陈学武.城市公共交通系统规划方法与管理技术［M］.北京:科学出版社，2002.

［6］李 丹，曲玉萍，王晓燕.城市公交乘车系统中的最优路线算法研究［J］.中国交通信息产业，2005(1).

［7］良 河，刘信斌，廖大庆.城市公交线路网络图的最短路与乘车路线问题［J］.数学的实践与认识，2004，34(6).

［8］西安市人大.西安市城市快速轨道交通建设规划［EB/OL］.http://www.china － xa.gov.cn/sites/MainSite/Detail.aspx?StructID=2890.

［9］西安市城市快速轨道交通线网规划报告［R］.2000.

［10］郭文莲，罗湘武.公交车辆隔站停车运行模式研究［J］.湖南交通科技，2008，34(4):155 －157.

［11］陈 芳.城市公交调度模型研究［J］.中南公路工程，2005，30(2):162－164.

［12］胡光明，雷红尧.博弈论在公交枢纽规划布局方案评价中的应用研究［J］.中南公路工程，2006，31(6):116 －118.

［13］李光辉，赵顺波.我国城市快速公交系统关键问题研究［J］.公路工程，2008，33(4):157 －160.