基于量子粒子群算法的MIMO信道容量优化

陈常山，张 申，魏 培

(中国矿业大学物联网研究中心;信息与电气工程学院，江苏 徐州 221000)

责任编辑:许 盈

MIMO可以在无需增加带宽的情况下，大幅提高信道容量，被认为是下一代无线通信的关键技术［1］。但在实际应用中MIMO信道容量受多方面的影响，很多学者对实际环境中MIMO信道容量的影响作了大量研究［2-7］，这些研究论文都从一个或几个方面对影响MIMO信道容量的因素进行了深入探讨，并据此给出了一些理论建议，这对于实际应用中尽可能达到最大容量是有益的。然而如何在实际中限制性条件下使MIMO信道容量最大化是一个要考虑的问题。本文综合考虑影响MIMO信道容量的因素，利用量子粒子群算法，在既定的条件下给出MIMO系统架构的最优方案。

1 MIMO信道容量影响因素

1.1 天线数量

MIMO信道容量是随着收发天线数的较小值成线性增加的关系［8-9］，图1是对MIMO在不同收发天线数目下的信道容量的仿真，其中Tx为发射天线数，Rx为接收天线数。

图1 不同收发天线数目下MIMO信道容量

由图1可以发现，相比较于传统的一发一收形式，MIMO的信道容量有了显著增加，但实际应用中空间和复杂度的限制，天线数目并不能无限扩展，这就需要在有限的条件下给出最合理的天线设计。

1.2 天线阵列结构

以线性天线阵为例，在不同的天线间隔，以及不同的扩展角条件下，MIMO的信道容量有较大差别［10-11］，因为这些因素都在不同程度上影响天线之间的相关性，而天线之间的相关性是决定MIMO信道容量的关键因素［12］，图2仿真的是不同相关系数下MIMO信道容量的比较，这里以2×2为例。

图2 不同相关系数下MIMO信道容量随信噪比的变化趋势

由图2可以看出，MIMO信道容量随着相关系数的增加变化较大。天线之间相关性受天线之间的间隔以及扩展角度等因素的影响，而这种影响并不是一个简单的增减函数［13］，这就需要在实际条件下仔细分析给出最优的架构。

1.3 天线高度

图3是接收端场强随发送端天线高度变化的趋势，这里假设接收端高为1.5 m。

图3 接收端场强随发送端高度的变化趋势

图3可以看出，接收端的场强不是随发送端天线高度成线性变化的，如果发射天线设计不合理极有可能造成接收端信号的极度衰弱。所以有必要结合实际情况所确定的高度范围对发送端天线进行合理的设计。

1.4 其他典型因素

除了以上提到的关键因素外，还有较多的重要因素影响MIMO的信道容量，在已知和未知信道状态信息的情况下，尤其是在天线数量较多时，MIMO信道容量差距较大［14］;而在巷道里，MIMO的信道容量又受巷道尺寸的影响［4］;不同的移动速度对MIMO信道容量有不同的影响程度［2］等，这些都是需要考虑的。

2 MIMO信道容量优化

透过以上的分析，发现有必要结合实际情况对MIMO的天线做合理的布置，但同时可以看到，MIMO信道容量受多方面的影响，要作出合理设计需要多点考虑。量子粒子群优化算法［15］在解决这类问题上具有很大优势。

量子粒子群算法是对传统粒子群算法的改进，由于引入了量子的概念，使得此算法具有更高的全局搜索能力，而且需要的参量更少。这里解决主要问题的有粒子的构造，这是最基本的，目的是要寻找最优的粒子;构建惩罚函数，以使得算法能按照既定的要求搜索最优粒子;得到粒子的搜索空间，这就要结合实际条件给出恰当的范围。

2.1 算法设计

首先要构造一个基本粒子 X(m1，m2，m3，m4，…) ，为了节省问题的处理，这里假定m1，m2，m3分别表示天线的间隔、天线高度、天线数目，其他因素可以再继续加上。

其次要构建一个惩罚函数，这是寻找粒子的依据，根据以上的分析，给出一个简单的公式

μ1，μ2分别表示影响因子;Imin是指M，N中的最小值所组成的单位矩阵;det(·)表示行列式;ξ是信噪比;H表示瑞利矩阵，HH表示H的共轭矩阵;λ，σ，ω，l分别表示波长、角能量分布的标准差、中心到达角以及天线间隔;p，d，r，λ，h1，h2分别表示发送端有效辐射功率、方向系数及收发天线间隔、波长以及收发天线高度;Q定义为［9］

再次，要根据实际情况给出粒子的范围，比如天线高度在50～100 m，天线允许间隔在0～20 cm，天线数目在2～4根，这样就给出了粒子的三维搜索空间。

这些基本的参数给出以后，初始化一群粒子，如X(2，60，3) ，X(3，58，2) ，X(5，63，3) 等，然后代入迭代公式［15］

式中:pbest，gbest，M分别为个体极值、全局极值以及总的粒子数;ε1，ε2，u分别是在0～1之间的随机数;η是收扩系数。根据式(3)就可以找出一系列的粒子，这里要用到惩罚函数以确定是否为最优粒子。最后根据粒子的范围以及粒子的精度或者迭代次数终止循环迭代，以找出最优的粒子。

2.2 仿真及分析

这里精确到小数后4位，迭代次数为100，然后对信噪比在0～30 dB之间的MIMO信道容量进行优化，同时再对得出的最优粒子进行比较，取其中数值最小的粒子作为最优粒子，这是由于惩罚函数的震荡性导致求出的最优粒子有多个，而其中的最小值代表着成本的最小值，因为数值越小表示高度越低，间隔越小，天线数目越少，这样可以减少信号处理和天线架设的成本。

依据上述条件得出最优粒子X(20，54.3749，4)，这表示天线间隔为20 cm，高度为54.3749 m，收发天线均为4根时为最优方案，这样根据得出的最优方案再对MIMO信道容量作计算，图4是优化前后的比较。

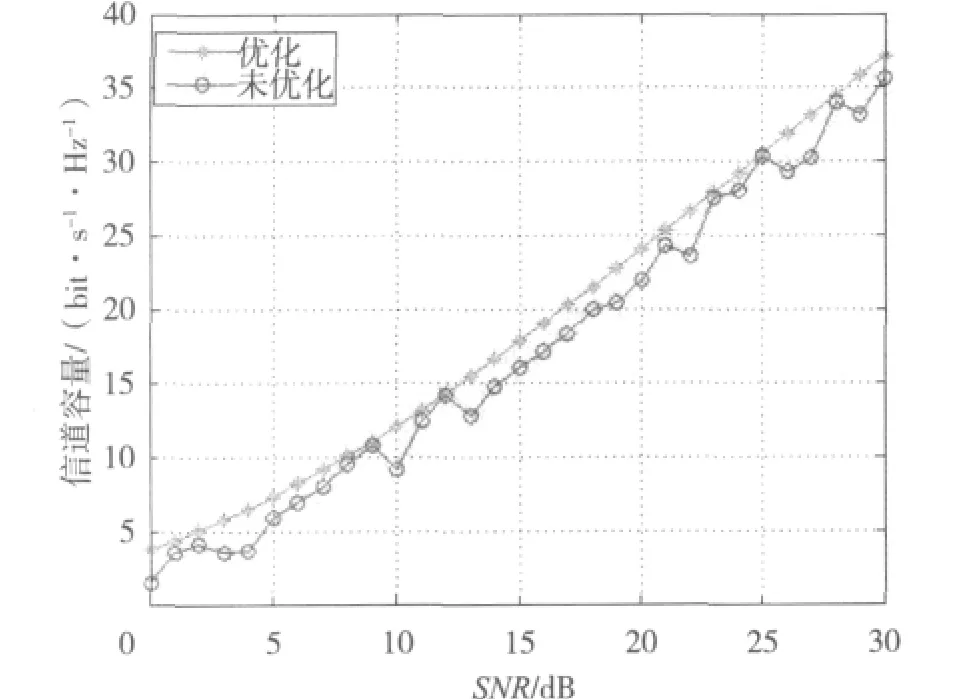
图4 MIMO信道容量优化前后比较

从图4可以看出，根据量子粒子群算法所得出的最优方案比未进行优化的MIMO信道容量有了较为明显的提高，而实际情况下若无优化，架设天线时很难人工准确找到最佳的方案，所以MIMO信道容量具有一定的随机性。虽然某些情况下未优化的MIMO信道容量也能达到最优值，但是其随机性较大，这会一定程度上影响通信的质量。而优化之后的MIMO信道容量稳定性较好，没有出现较大的跳跃性，这对实际的应用是有利的。

3 结论

MIMO作为下一代无线通信的关键技术，具有很高的信道容量，但是实现其高容量受到很多方面的限制。本文综合考虑影响MIMO信道容量的各个因素，并给出了其中几个关键因素的仿真情况，透过这些仿真发现，要实现MIMO高信道容量需要对天线根据实际情况作出合理的设计布置。据此，依据量子粒子群优化算法，给出了其中的惩罚函数，并构造了基本粒子，这样根据算法的迭代函数，就可以求出最佳粒子，依据此最佳粒子可以对天线做合理的优化布置。本文中给出的参数中有几个是与MIMO信道容量成正比的，这会很大程度上影响量子粒子群算法的优势，然而在实际情况中，影响MIMO信道容量很多的因素是与其成一定的函数关系，而不是正比例关系，所以本文给出优化算法对此类问题的处理有一定的参考意义。

［1］MARZETTA T L，HOCHWALD B M.Capacity of a mobile multiple-antenna communication link in Rayleigh flat fading［J］.IEEE Trans.Commun.，1998，46(7):870-880.

［2］李忻，聂在平，伍裕江.移动性对MIMO无线信道性能的影响［J］.电子科技大学学报，2004，33(5):504-506.

［3］李忻，聂在平.天线阵列方位对MIMO无线信道性能的影响［J］.电子与信息学报，2005，27(9):1433-1436.

［4］郑红党.煤矿井巷电波传播理论和MIMO信道建模关键技术研究［D］.徐州:中国矿业大学，2010.

［5］孙继禹，谢红.MIMO信道在不同条件下的容量分析［J］.传感器与微系统，2011，30(12):50-53.

［6］李英梅，邵玉斌，王纯.不同天线相关分布特性下的M IMO容量性能分析［J］.云南民族大学学报:自然科学版，2007，16(3):277-280.

［7］吕剑刚，吕英华，李云庄，等.天线阵结构对非视距室内MIMO信道容量的影响［J］.电子与信息学报，2006，28(9):1636-1639.

［8］FOSCHINI G J，GANS M J.On limits of wireless communication in a fading environment when using multiple antennas［J］.Wireless Personal Communication，1998，6(3):311-335.

［9］VUCETIC B，YUAN J.Space-time coding［M］.［S.l.］:John Wiley ＆Sons Ltd.，2003.

［10］庞继勇，李建东，赵林靖.MIMO相关信道估计中训练序列的最优结构和最佳长度［J］.电子学报，2007，35(6A):35-40.

［11］CHIZHIK D，RASHID-FARROKHI F，LING J，et al.Effect of antenna separation on the capacity of BLAST in correlated channels［J］.IEEE Comm.Lett，2000，4(11):337-339.

［12］康桂华.MIMO无线通信原理及应用［M］.北京:电子工业出版社，2009.

［13］吕波.MIMO空间相关性近似算法及性能研究［D］.南京:南京信息工程大学，2011.

［14］李莉，王珂，韩力.CSI对MIMO系统信道容量影响的仿真与分析［J］.武汉理工大学学报:信息与管理工程版，2007，29(7):1-4.

［15］SUN Jun，FENG Bin，XU Wenbo.Paticle swarm optimization with particles having quantum behavior［C］//Proc.IEEE Congress on Evolutionary Computation.Portland:IEEE Press，2004:325-331.