一种新的基于分块直方图的Mean－Shift跟踪算法

李群山，张 文

（1.电子科技大学光电信息学院，四川成都610054;2.内江师范学院工程技术学院，四川内江 641112）

目标跟踪是计算机视觉和图像处理研究中的一个重要课题，其广泛应用于智能视频监控、军事制导、智能机器人等视觉应用领域［1-2］。目标的颜色直方图具有特征稳定、抗部分遮挡、计算方法简单和计算量小的特点，基于Mean-Shift的跟踪一般采用直方图对目标进行建模，然后通过相似度度量，最终实现目标的匹配和跟踪［1］。

均值漂移算法（Mean-Shift）是一种基于密度梯度上升的非参数方法，通过较少的几次迭代运算就能找到目标位置。这种算法计算量小、计算速度快，体现出良好的实时性和稳定性，适用于实时视频的目标跟踪。经典的Mean-Shift跟踪算法用于目标建模的颜色直方图只是包含了颜色特征在目标中出现的概率信息，没有融入目标的空间信息［3-7］。梁静等人利用kalman滤波器和Mean-Shift相结合的方法跟踪动态背景下的运动目标，解决了目标被部分遮挡的情况［8-11］。

目标的颜色通常分布在颜色空间的一个子空间，传统的颜色直方图通常将颜色空间均匀划分（例如16×16×16或者32×32×32），这样容易造成大量的空的颜色直方图区间，不仅浪费内存空间，而且还增加了计算量。针对传统颜色直方图空闲率高，本文提出了简化颜色直方图的方法，针对传统颜色直方图没有融入空间信息的缺点，提出了一种新的分块直方图构建方法，这种分块直方图构建方法简单，而且保留了颜色直方图的尺度和旋转变化的不变性。

1 经典Mean-Shift算法

1.1 目标模型

设{xi}，i=1，2，…，n表示目标区域归一化的n个像素集，x0为目标区域的中心像素点。将颜色特征空间划分成u=1，2，…，m个子空间，也就是直方图上的m个bin。每个特征u=1，2，…，m在目标区域的概率值为

假设候选目标模型的在t时刻的中心位置为y;{xi}，i=1，2，…，Nb表示候选目标区域的像素集，则相应候选目标模型在特征值u=1，2，…，m出现的概率可以表示为

1.2 相似性度量

经典的Mean-Shift使用Bhattacharry系数度量目标模型与候选目标模型（y）之间的相似性。相似性定义为

跟踪过程就是不断获得与目标模型相似性最大的候选模型的过程，即求取式（3）最大值的过程。为求式（3）的最大值，令式（3）在（y0）处进行Taylor式展开，并省略一些极小项，得

将式（2）代入式（4）得

要使式（3）最大也就是要使得式（5）最大，而式（5）的第一项为常量，则第二项最大时式（5）最大。结合Mean-Shift算法，得迭代公式为

式中，g（x）=－K'（x）。如果使用Epanechniko核函数，则（7）式进一步简化为

Mean-Shift算法的计算步骤:首先初始化y0，可令y0为最初的目标中心;然后用式（6）计算wi，并利用式（7）计算获得下一次迭代的位置;令y0=y1，进行下一次迭代运算，如此不断地迭代计算式（6），（7），直到‖yi+1－yi‖ ＜ε，或达到最大迭代次数。最终由式（7）得到的位置就是目标的准确位置。

2 改进的Mean-Shift算法

2.1 目标颜色直方图的简化

在建立目标颜色直方图之前通常需要将颜色空间进行量化，目前一般采用均匀量化颜色空间的方法，这样可以减少计算量。但是目标颜色通常紧凑分布在颜色空间的一部分子空间中，因而会造成大量空的颜色直方图区间，或者取值极小的颜色直方图区间。这样不仅会浪费大量的内存空间，而且增加计算量。例如:图1是经常遇到的人脸跟踪目标，其颜色直方图在16×16×16均匀量化的RGB颜色空间中，空的直方图区间达到3 878个，空闲率达3 878/4 096=94.7%。若为这些空的直方图区间分配内存空间，按存储类型为双精度浮点型（8 byte）计算将是31 024 byte。若是在32×32×32量化空间，则空区间为32 550，空闲率达=32 550/32 768=99.3%，浪费的内存空间将是260 400 byte。图2（图2～图11彩色图见网址:http://blog.sina.com.cn/s/blog_b9be7b8501017gyc.html）色彩如此丰富，其在16×16×16均匀量化的RGB颜色空间中空的直方图区间也达3 400个，空闲率为3 400/4 096=83%。而且在跟踪过程中计算Bhattacharry系数时，为其还要付出一定的计算代价。

针对颜色直方图空闲率非常高的情况，本文提出简化颜色直方图的方法，得到没有空闲区间的直方图;同时为了应对在计算候选目标颜色直方图时会出现不同于初始跟踪目标颜色特征的像素的情况，在简化的颜色直方图后增加一个区间用于累积非初始跟踪目标颜色特征的像素。其计算步骤如下:

1）按照传统方法统计得到颜色直方图，并去除空直方图区间。

2）保存剩下的颜色直方图区间对应的颜色特征值。

3）在经过上面处理后的直方后增加一个区间，用于累积候选目标中出现的非初始目标颜色特征的像素。在初始目标的直方图中该区间的值为0，在候选目标的直方图中该区间的值为所有不属于初始目标颜色特征的像素总和归一化后的值。

2.2 空间颜色直方图的建立

假设某目标Q的大小为N（即总像素点），f（x，y）是该目标中的一点，f（x，y）表示目标在该点的颜色值，（x，y）表示该点的坐标，则其质心为

该目标中离该质心（x0，y0）最大的距离为

图3 图像空间划分示意图

最后，根据前面颜色空间量化结果得到的m个颜色子特征空间，分别计算每个圆环区域内的传统颜色直方图，得到最终的分块颜色直方图。其中第v个子空间的第u个颜色特征值为

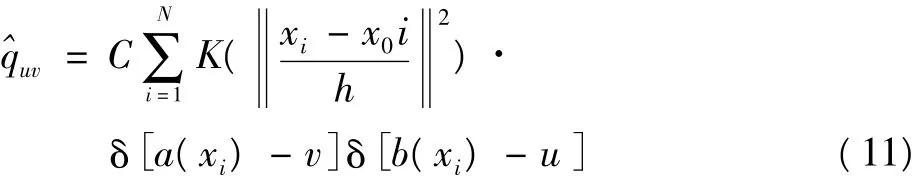
式中:a（xi）表示该像素距离质心的量化空间距离;δ［a（xi）－v］是Kronecker delta函数，当该像素属于第v个空间圆环时，函数值为1，否则为0。其他参数与传统颜色直方图相同。于是，目标模型可表示为:q={quv}，u=1，2，…，m;v=1，2，…，w 。这样得到的分块颜色直方图具有以往分块直方图不具有的尺度、旋转不变性。

2.3 新分块直方图与传统颜色直方图的比较

为了验证新分块直方图的优点，下面对两个颜色分布相似物体的传统颜色直方图与新颜色空间直方图进行比较，来验证新分块直方图具有更好地区分颜色分布相似目标的优点。图4、图5表示颜色分布相似的两个目标;图6、图7分别是图4、图5的传统颜色直方图;图8、图9分别是图4、图5的分块颜色直方图。为了显示方便，以下的颜色直方图在HSV颜色空间统计得到，归一化系数为直方图中区间值的最大值，分块颜色直方图的圆环数仅为3个。

利用Bhattacharry系数度量图6与图7之间的相似程度为0.98，而图8与图9之间的相似程度仅为0.80。可以看出新颜色直方图有更好地区分颜色分布相似目标的能力。为了加大区分度可增加分块的圆环数。

2.4 改进后的Mean-Shift算法

根据分块直方图的计算方法不同，改进后的Mean-Shift算法的Bhattacharry系数计算式为

将式（11）代入式（12）整理得

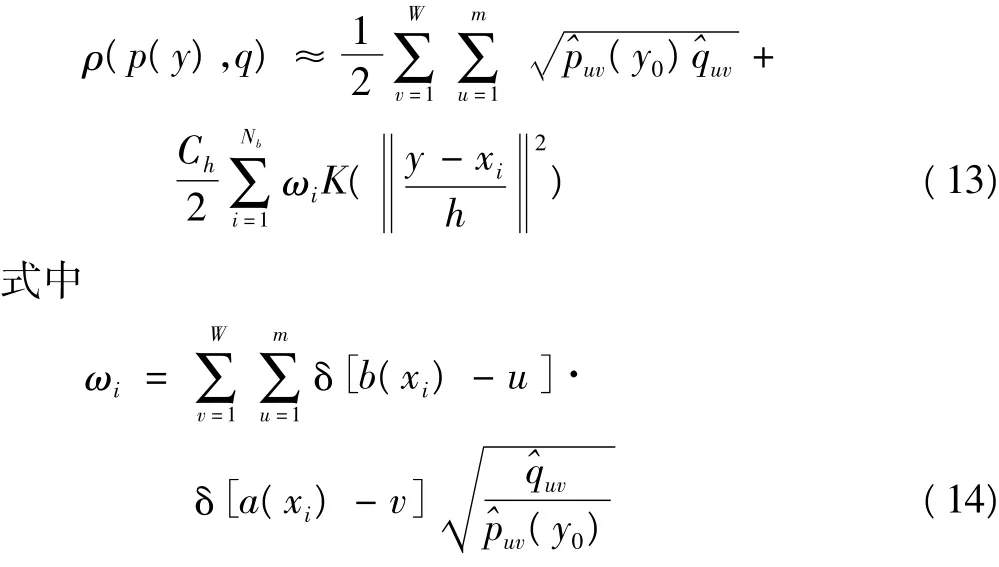
Meanshift算法的其他计算公式不变。

3 实验结果

本文的所有实验在VS2008环境下及利用OpenCV完成，主机主频1.9 GHz，内存1 Gbyte。在RGB颜色空间计算颜色直方图，颜色空间量化为16×16×16的子空间，目标的初始化手动完成，真值的标注也由手动完成。为了适应尺度的变化，进行增量正负10%的核窗宽调整。

3.1 实验一

实验视频在办公室环境拍摄，为了构造颜色分布相似的目标，实验中利用魔方作为跟踪对象。视频图像大小为640×480。实验视频拍摄的是魔方的变速运动及尺度变化的情形。实验结果如图10所示。跟踪目标在X，Y坐标轴上的误差统计结果如图11所示。实验画面中的红色框为改进后算法跟踪结果，白色框为经典Mean-Shift算法跟踪结果。

分析图10和图11可看出改进后的Mean-Shift算法比经典算法跟踪目标更加准确，主要原因是分块直方图中融入了空间信息，使其描述目标的能力比传统颜色直方图更准确。

3.2 实验二

实验所用视频拍摄的是两个颜色分布相似魔方存在遮挡的情形。其中一个魔方静止，另一个魔方运动。图12的跟踪试验中，跟踪的目标为运动的魔方，运动魔方逐渐运动到静止魔方背后被遮挡的情形。图13的跟踪实验中，跟踪目标是静止魔方，在实验中逐渐被运动魔方遮挡的情形。实验画面中的红色框为改进Mean-Shift算法跟踪结果，白色框为经典Mean-Shift算法跟踪结果。

在图12实验中，在运动魔方被静止魔方遮挡后再从静止魔方后面运动出来时，白色框（经典Mean-Shift算法跟踪结果）跟踪丢失，停留在静止魔方上;而红色框（改进Mean-Shift算法跟踪结果）却能正确地进行跟踪。

图12 运动目标被遮挡跟踪实验

图13 静止目标被遮挡跟踪实验

在图13实验中，运动魔方逐渐从静止魔方前面经过，并完全遮挡了后面静止的魔方，随着运动的进行，当被遮挡的静止魔方逐渐显现出来时，白色框（经典Mean-Shift算法跟踪结果）跟踪丢失，跟踪到颜色相似的运动魔方上;而红色框（改进Mean-Shift算法跟踪结果）却能停留在了静止魔方上，表示跟踪正确。

4 结语

本文针对颜色直方图空闲率高造成的内存空间的浪费问题提出了一种简化颜色直方图的计算方法，并提出了一种新的分块颜色直方图的构造方法。实验结果表明基于新的分块直方图的Mean-Shift跟踪算法比经典的Mean-Shift算法具有更好的跟踪稳定性，在跟踪颜色分布相似的目标方面，特别是在相似目标出现大部分遮挡情况下仍能稳定地跟踪目标，与经典Mean-Shift算法相比具有更稳定的效果。

：

［1］宋新，沈振康，王平，等.Mean-Shift在目标跟踪中的应用［J］.系统工程与电子技术，2007，29（9）:1405-1409.

［2］李培华.一种改进的Mean-Shift跟踪算法［J］.自动化学报，2007，33（4）:347-354.

［3］FUKUNAGA K，HOSTETLER L.Estimation of the gradient of a density function and its applications in pattern recognition［J］.IEEE Trans.Information Theory，1975，21（1）:32-40.

［4］CHENG Yizong.Mean shift，mode seeking，and clustering［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，1995，17（8）:790-799.

［5］COMANICIU D，MEER P.Mean shift:a robust approach toward feature space analysis［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2002，24（5）:603-619.

［6］COMANICIU D，RAMESH V，MEER P.Kernel-based object tracking［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2003，25（5）:564-577.

［7］COMANICIU D，RAMESH V，MEET P.Real-time tracking of non-rigid objects using mean shift［C］//Proc.IEEE Conference on Computer Vision and Pattern Recogniton，2000.［S.l.］:IEEE Press，2000:142-149.

［8］YILMAZ A，SHAFIQUE K，SHAH M.Target tracking in airborne forward looking infrared imagery［J］.Image and Vision Computing，2003（21）:623-635.

［9］BIRCHFIELD S T，RANGARAJAN S.Spatiograms versus histograms for region-based tracking［C］//Proc.Computer Vision and Pattern Recognition，2005.［S.l.］:IEEE Press，2005:1158-1163.

［10］袁光林，薛模根，谢恺，等.多颜色直方图自适应组合mean shift跟踪［J］.中国图象图形学报，2011，16（10）:1832-1840.

［11］梁静，支琤，周军.基于mean shift的抗遮挡运动目标跟踪算法［J］.电视技术，2008，32（12）:82-85.