沥青路面线性疲劳损伤特性及形变规律

孙志林 黄晓明

(1长沙理工大学公路工程教育部重点实验室，长沙410114)

(2东南大学交通学院，南京210096)

沥青路面疲劳破坏机理一直是研究的热点，相关学者利用断裂力学、损伤力学、现象学等方法针对沥青路面疲劳破坏作了大量研究［1-4］.但针对沥青路面结构疲劳破坏过程的研究较少，特别是系统采用损伤力学-有限元全耦合方法针对沥青路面结构在交通荷载作用下的疲劳损伤过程的研究更少［5-8］.为了准确分析沥青路面结构疲劳损伤过程，本文将运用损伤力学-有限元全耦合方法，基于通用有限元软件ABAQUS计算平台及相应用户材料子程序UMAT，分析沥青路面结构在车辆荷载作用下路面结构损伤度演变规律，以及应变状态与路表弯沉随荷载作用的变化规律.相关研究结论将为沥青路面结构设计、维修养护及沥青路面长期性能预测提供理论依据.

1 疲劳损伤有限元方法

在疲劳损伤力学理论中，Miner模型是一个广泛应用的线性损伤演化模型，其损伤演化方程为

式中，D为损伤度，本文中取0≤D≤0.5;K，m为回归系数，与材料种类有关;N为荷载作用次数(疲劳寿命);σ为应力水平，本文中为水平正应力.

本文中有限元计算模型选择平面应变模型，此时有限元方法的本构方程为

式中，E 为弹性模量;μ 为泊松比;σx，σz，τxz为应力分量;εx，εz，γxz为应变分量.

为了准确地进行损伤力学有限元疲劳损伤累积分析，本文采用全耦合方法，即每隔一定的应力循环次数进行单元刚度矩阵的重新计算，以反映疲劳损伤累积效应对单元刚度矩阵的影响.在有限元软件ABAQUS提供的用户子程序接口上，采用FORTRAN77编写用户子程序UMAT，以反映疲劳损伤对单元刚度的影响，即耦合疲劳损伤的材料模型进行相应的编译连接，用于进行疲劳损伤分析.本文所用计算方法中，用户子程序UMAT中的单元刚度矩阵在每个增量步中都进行调用，每次调用之后按照疲劳损伤演化规律及时更新刚度矩阵中的疲劳损伤度D，因此该方法属于全耦合解法，其准确度高于全解耦和半耦合解法，且具有明确的物理意义.

2 结构计算模型

2.1 路面结构

采用我国目前常用的半刚性路面结构形式.路面结构各组成部分的材料如下:面层材料为沥青混凝土，基层材料为水泥稳定碎石，底基层材料为二灰土.各层材料的具体参数见表1.

表1 路面结构计算参数

本文中有限元计算模型为平面应变模型，尺寸为10 m×10 m.假定模型两侧与底部完全约束，路面表面为自由面，没有约束.由于靠近约束边界的位置各种力学响应很小，可忽略不计，因此假定是合理的.

2.2 材料疲劳损伤参数

依据相关文献提供的大量疲劳试验结果，考虑现场因素［9-11］，经计算得到Miner损伤演化方程的疲劳参数，如表2所示.

表2 Miner疲劳损伤模型参数

2.3 荷载条件

选取车辆荷载宽度W=156 mm，双轮中心距B=312 mm.为了保证施加荷载为标准轴载，选取荷载集度P=0.16 MPa.这样的设定能够保证在相同路面结构组合下各层结构的应力水平与标准轴载基本相同，路表弯沉在通常范围内，不影响结构各种响应的规律性分析.

3 损伤场分析

3.1 损伤度空间分布规律

利用ABAQUS有限元计算软件，计算可得沥青路面结构在车辆荷载作用6×106次后的损伤度空间分布规律.其中，图1为双轮中心线下垂直方向基层与底基层损伤度分布规律，图2为基层与底基层层底沿水平方向损伤度分布规律.

图1 双轮中心线下基层与底基层损伤度

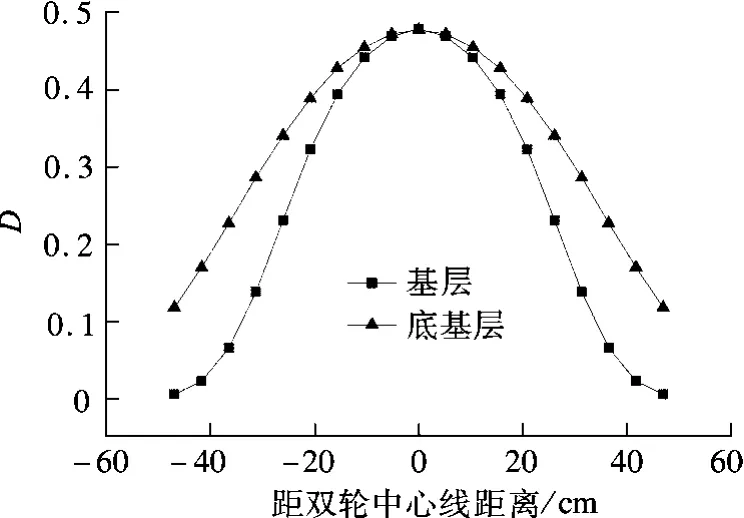
图2 基层与底基层层底损伤度

从图1可看出，在双轮中心线下，无论是基层还是底基层，均是越靠近层底损伤度越大，从层底往上逐渐减小.这是因为在达到一定损伤度之前，越靠近层底，水平拉应力越大，从而形成的损伤也就越大.对于基层，在距层底约10 cm处，损伤度变为0，这是由于基层上部位置已经出现压应力，没有拉应力形成的损伤，因此基层的损伤主要集中在靠近层底的位置.从基层层底往上，损伤度递减的幅度有所减小.对于底基层，损伤度自下往上逐步递减，直到接近层顶的位置损伤度才接近0，这主要是因为对于底基层，整个结构层从下至上都处于拉应力状态，因此从下至上均会出现损伤.从层底往上，损伤度减小的幅度开始时逐渐增大，然后逐渐减小，拐点出现在距层底15 cm左右的位置.

从图2中可看出，损伤度最大的位置出现在双轮中心线下，往两侧损伤度逐渐减小，这与双轮中心线下层底拉应力分布相吻合，说明该位置是整个结构最先出现破坏的地方，当损伤达到一定的程度，便会在此位置逐渐形成裂纹直至开展形成宏观裂缝.对于基层，在中心线两侧附近，损伤度往两侧减小的幅度逐步增大，损伤度迅速减小，到一定的位置后损伤度减小的幅度减缓.底基层的损伤度有类似的规律.由此可见，损伤主要分布在中心线两侧附近.

3.2 结构层层底损伤度随荷载作用次数的变化

图3给出了沥青路面结构层底损伤度随荷载作用次数的变化规律.由图3可看出，基层层底的损伤度随荷载作用次数增加而增加.当荷载作用次数从0增加到5×105次时，基层层底损伤度由0增加到0.222，当荷载从6.5×106次增加到7×106次时，损伤度增加了7×10－3.可明显看出，随着荷载次数的增加，损伤度增加的幅度越来越小.底基层损伤度在初始阶段其增长速度要小于基层;荷载作用次数从0增加到5×105次时，底基层层底损伤度由0增加到0.2;但后期增长速度相近，当荷载从6.5×106次增加到7×106次时，损伤度也增加了7 ×10－3.

图3 层底损伤度随荷载作用次数的变化规律

本文选用了Miner线性疲劳损伤演化模型，但层底损伤度随荷载作用次数的变化并不是线性增长的.这是因为在分析中考虑了损伤度与应力的耦合作用，即当路面结构在水平拉应力作用下产生损伤后，结构模量发生改变，相应的应力分布也发生改变，所以损伤已经不是在常应力下发生的，因此由Miner线性疲劳损伤演化模型的公式可以看出，损伤度随荷载作用次数的变化也就不是线性变化.实际上分析点的应力在逐渐减小，因此损伤度的增长会逐渐减小.

4 应变场分析

4.1 路面结构水平正应变空间分布规律

沥青路面结构在车辆荷载作用6×106次后，其水平正应变空间分布规律如图4和图5所示.其中，图4为双轮中心线下垂直方向基层与底基层水平正应变分布规律，图5为基层与底基层层底沿水平方向水平正应变分布规律.

从图4可看出，基层与底基层双轮中心线下水平正应变沿竖向分布规律与无损路面结构没有差别，但靠近层底拉应变增大，沿竖向增大幅度线性减小，中性轴上移，这与相关解析解的分析结果一致［12］.从图5可看出，基层与底基层层底水平正应变分布规律与无损路面结构的分析［12］相比较，无明显差异，但整体数值较大，且越靠近双轮中心，增大越多.由上述分析可知，沿竖向与水平向水平正应变均有所改变，这主要是由于路面结构受损后，整个结构刚度降低，弯拉程度更为严重，导致整个结构应变增大.

图4 双轮中心线下基层与底基层水平正应变

图5 基层与底基层层底水平正应变

4.2 路面结构各层层底水平正应变随荷载作用次数的变化

图6 层底水平正应变随荷载作用次数的变化

分析路面结构在车辆荷载作用下，结构层底水平正应变随荷载作用次数增加的演化规律，其结果如图6所示.从图中可看出，基层与底基层层底拉应变均随荷载作用次数的增加而增加，但增加幅度逐渐减小，这与损伤度随时间的演化规律一致.出现这种现象的原因是由于随着损伤增大，导致结构刚度降低，结构弯拉程度增大.可以看出，与无损路面结构层底拉应变分析［12］相比较，考虑线性疲劳损伤的路面结构层底拉应变均随着荷载作用次数在改变，而不是定值.

5 路表弯沉分析

分析沥青路面结构在车辆荷载作用下，路表弯沉随荷载作用次数增加的演化规律，其结果如图7所示.从图7可看出，随着荷载作用次数的增加，路表弯沉不断增加，但增加的幅度逐渐减小.可以发现，路表弯沉随荷载作用次数变化的规律与结构层底损伤度的变化规律一致.这是因为随着荷载作用次数的增加，层底的损伤增加，且增加的幅度逐渐减小，导致模量按照一定规律减小，相应的路表弯沉就会增加，增加的幅度逐渐减小.由于路面弯沉与结构应变具有一一对应的关系，因此可以看出路表弯沉的变化规律与层底拉应变的变化规律一致.

图7 路表弯沉随荷载作用次数的变化

6 结论

1)路面结构的损伤主要分布在双轮中心线下靠近层底的区域;随着车辆荷载作用次数的增加，基层层底与底基层层底的损伤度增加，但增加的幅度逐渐减小.依据结构损伤度分析，可以实时了解结构在不同时期、不同位置损伤度的分布和损伤程度，从而确定对路面结构进行养护维修的时间和位置，以及采用的措施.

2)当考虑路面损伤时，路面结构层内水平正应变随着荷载作用而改变，靠近层底位置拉应变增大，中性轴上移.层底拉应变随荷载作用次数的增加而增加，但增加幅度逐渐减小.

3)由于路面结构的损伤，随着车辆荷载作用次数增加，路表弯沉逐渐增大，但增大幅度逐渐减小.依据该结论可对路表弯沉变化规律进行预测，从而研究基于路表弯沉的沥青路面长期性能.

References)

［1］Carpenter S H，Ghuzlan K A，Shen S.Fatigue endurance limit for highway and airport pavements［J］.Transportation Research Record，2003，1832:131-138.

［2］Lytton R L，Chen C W，Little D N.Microdamage healing in asphalt and asphalt concrete，volumeⅣ:a viscoelastic continuum damage fatigue model of asphalt concrete with microdamage healing［R］.Texas，USA:Transportation Institute，2001:178.

［3］Park S W，Kim Y R，Schapery R A.A viscoelastic continuum damage model and its application to uniaxial behavior of asphalt concrete［J］.Mechanics of Materials，1996，24(4):241-255.

［4］Chaboche J L，Lesne S M.A non-linear continuous fatigue damage model［J］.Fatigue and Fracture of Engineering Materials and Structure，1988，11(1):1-17.

［5］杨永顺，王林，高雪池，等.永久路面结构应变分布及疲劳损伤分析［J］.山东大学学报:工学版，2009，39(2):118-124.Yang Yongshun， WangLin， GaoXuechi， et al.Analysis of perpetual pavement strain distribution and fatigue damage［J］.Journal of Shandong University:Engineering Science，2009，39(2):118-124.(in Chinese)

［6］刘振清，钱国超，刘清泉，等.设ATPB的半刚性基层沥青路面结构疲劳特性分析［J］.中国公路学报，2008，21(5):15-18.Liu Zhenqing，Qian Guochao，Liu Qingquan，et al.Analysis of fatigue characteristic of semi-rigid base asphalt pavement structure with ATPB ［J］.China Journal of Highway and Transport，2008，21(5):15-18.(in Chinese)

［7］Shu Xiang，Huang Baoshan，Vukosavljevic D.Laboratory evaluation of fatigue characteristics of recycled asphalt mixture［J］.Construction and Building Materials，2008，22(7):1323-1330.

［8］Sun Injun.Damage analysis in asphalt concrete mixtures based on parameter relationships［D］.Texas，USA:Texas A＆M University，2004.

［9］孙荣山，汪水银.级配变化对水泥稳定碎石材料疲劳性能影响的研究［J］.公路交通科技，2007，24(6):57-61.Sun Rongshan，Wang Shuiyin.Research on fatigue performance of the different gradation of cement stabilized crushed stone［J］.Journal of Highway and Transportation Research and Development，2007，24(6):57-61.(in Chinese)

［10］许志鸿，李淑明，高英，等.沥青混合料疲劳性能研究［J］.交通运输工程学报，2001，1(1):20-24.Xu Zhihong，Li Shuming，Gao Ying，et al.Research on fatigue characteristic of asphalt mixture［J］.Journal of Traffic and Transportation Engineering，2001，1(1):20-24.(in Chinese)

［11］中华人民共和国交通部.JTJ 014—97公路沥青路面设计规范［S］.北京:人民交通出版社，1997.

［12］孙志林.基于损伤力学的沥青路面疲劳损伤研究［D］.南京:东南大学交通学院，2008.