A New Oscillation Criterion for Second-order Neutral Delay Differential Equations

YU Jin-chang DENG Li-hu LIU Xue-jie

(1.Computer College，Dongguan University of Technology，Dongguan 523808，China;2.Editorial Department of Journal，Dongguan University of Technology，Dongguan 523808，China)

In this paper，we study the problem of oscillation for second-order delay differential equations with nonlinear neutral term:

Throughout，we suppose that the functions and parameters in(1)satisfy the following conditions:

(A5)f∈C(R，R)and there exists a positive constant α such that

Neutral differential equations find numerous applications in natural science and technology. For instance，they are frequently used for the study of distributed networks containing lossless transmission lines;See Hale［1］.

In the last decades，there are many studies that have been made on the oscillatory behavior of solutions of differential equations［2－6］and neutral delay differential equations［7－18］.

For instance，Grammatikopoulos et al.［9］examined the oscillation of second-order neutral delay differential equations

where 0≤p(t)＜1.

Liu and Bai［12］investigated the second-order neutral differential equations

where 0≤p(t)＜1.

Ye and Xu［16］considered the second-order quasilinear neutral delay differential equations

where Z(t)=x(t)+p(t)x(τ(t))，0≤p(t)＜1.

Zafer［17］discussed oscillation criteria for the equations

where 0≤p(t)＜1.

Zhang et al.［18］considered the oscillation of even-order nonlinear neutral differential equations

where 0≤p(t)＜1.

To the best of our knowledge，the above oscillation results cannot be applied when p(t)＞1，and it seems to have few oscillation results for(1)when p(t)＞1.

Xu and Xia［14］established some new oscillation criteria for the second-order neutral delay differential equations

Motivated by Liu and Bai［12］，we will further the investigation and offer some more general new oscillation criteria for equation(1)，by employing a class of functionsand operator A. The method used in this paper is different from［14］.

Following ref.［12］，we say that a function φ =φ(t，s，l)belongs to the functions，if φ∈C(E，R)，where E={(t，s，l):t0≤l≤s≤l ＜∞}，which satisfies

for l ＜s ＜t and has the partial derivativesuch thatis locally integrable with respect to s in E.

By choosing the special function φ，we can derive some oscillation criteria for a wide range of differential equation.

Define the operator A［·;l，t］by

for t≥s≥l≥t0and g∈C(［t0，∞)，R). The function φ=φ(t，s，l)is defined by

It is easy to verify that A［·;l，t］is a linear operator and that is satisfies

1 Main Results

In this section，we give a new oscillation criterion for the equation(1). The following lemma will be needed in proving our results.

Lemma 1 Suppose that x is an eventually positive solution of equation(1). Let Z(t)=x(t)+c(t，x(tτ)). Then there exists a number t1≥t0such that for t≥t0，

Proof Let x(t)be an eventually positive solution of equation(1). Note that in view of(A4)and(A5)，there exists a number t1≥t0such that

From(1)，we also have Z(t)＞0 and［r(t)Z'(t)］'≤0 for t≥t1.

Next，we show that Z'(t)＞0 for t≥t1. In fact，if there exists a number t2≥t1such that Z'(t2)＜0.Then，noting that r(t)Z'(t)is decreasing，we have

Dividing both sides by r(t)＞0，we obtain

Integrating the above inequality from t2to t leads to

In view of(A1)，if follows from(14)that Z(t)takes on negative values for sufficiently large values of t.Since this contradicts the fact that Z(t)is eventually positive，we must have Z'(t)＞0 for t≥t1.

Theorem 2 Assume that τ≥σ. Further，there exist functions φ∈and k∈C1(［t0，∞)，R+)，such that

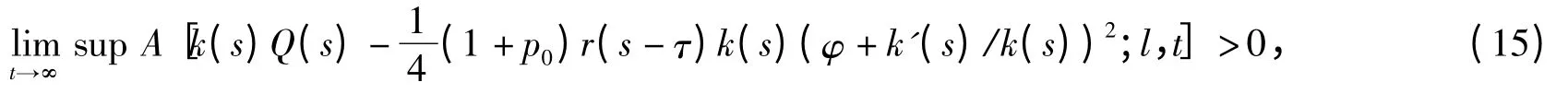
where Q(t)=min{αq(t)，αq(t－τ)}，the operator A is defined in(10)and φ=φ(t，s，l)is defined in(11).Then every solution of the equation(1)is oscillatory.

Proof Let x(t)be a non-oscillatory solution of equation(1). Then there exists t1≥t0such that x(t)≠0 for all t≥t1. Without loss of generality，we may assume that x(t)＞0，x(t－τ)＞0 and x(t－σ)＞0 for t≥t1.Let Z(t)=x(t)+c(t，x(t－τ)). By Lemma 1，there exists t2≥t1such that(13)holds for all t≥t2. From the condition(A5)and(1)，we get for sufficiently large t，

and

From(16)，(17)and(A3)，we have

Thus，we get

where Q(t)=min{αq(t)，αq(t－τ)}.

Define

Then w(t)＞0 and

From(20)and(21)， note that r(t－τ)Z'(t－τ)≥r(t)Z'(t)，we obtain

Similarly，define

Then v(t)＞0 and

From(23)and(24)，we obtain

Therefore，from(22)and(25)，we get

It follows from τ≥σ and Z'(t)＞0 that Z(t－σ)≥Z(t－τ)，then from(19)and(26)we get

Applying A［·;l，t］to(27)，we have

It follows from(12)and(28)that

Hence，from(29)，we have

that is，

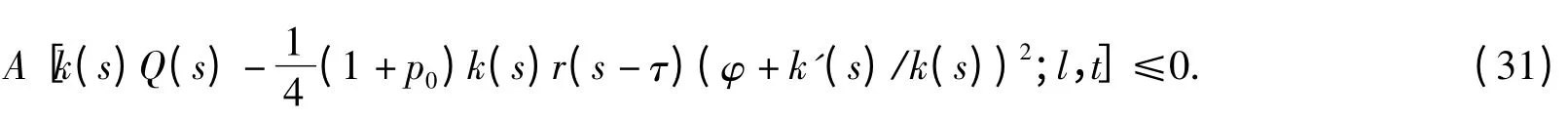
Taking the super limit in the above inequality，we get

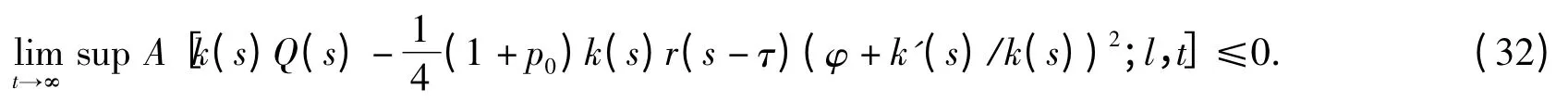
Which contradicts(15)and the proof of Theorem 1 is complete.

Remark 1 With the different choice of k and φ，Theorem 1 can be stated with different conditions for oscillation of(1). For example，if we choose φ(t，s，l)=ρ(s)(t－s)ν(s－l)μfor ν ＞1 2 ，μ ＞12 a nd ρ∉C1(［t0，∞)，R+)，then

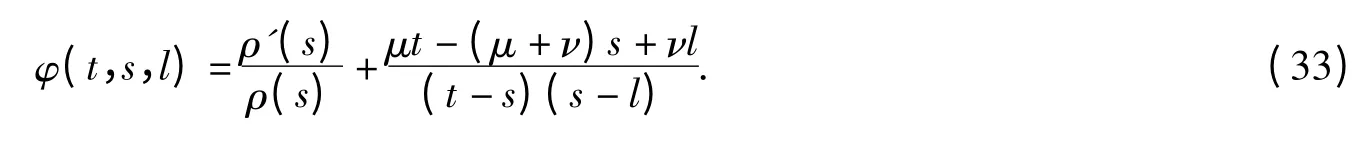
By Theorem 1，we can obtain the oscillation criterion for equation(1);the details are left to the reader.

For illustration，we consider an example.

Example Consider the following equation

where

Let φ(t，s，l)=(t－s)(s－l)，it is easy to verify that

By Theorem 1 let k(t)≡1，α=1 and Q(t)≡1，we can verify that(15)holds. Hence，every solution of equation(34)is oscillatory.

Acknowledgements The authors would like to express his gratitude to Professor Wen Lizhi and Professor Xu Zhiting for a number of suggestions that made the authors complete this paper.

［1］Hale J. Theory of Functional Differential Equations［M］. New york:Springer-Verlag，1977.

［2］Dzurina J，Stavroulakis I P. Oscillation criteria for second-order delay differential equations［J］. Appl Math Comput，2003，140(2－3):445－453.

［3］Grace S R. Oscillation theorems for nonlinear differential equations of second order［J］. J Math Anal Appl，1992，171(1):220－241.

［4］Koplatadze R. On oscillatory properties of solutions of functional differential equations［J］. Memoirs Diff Eqs Math Phys，1994 ，3:1－180.

［5］Philos Ch G. A new criterion for the oscillatory and aymptotic behavior of delay differential equations［J］. Bulletin de I’Academie Polonaise des Science，Serie des Science Mathematiques，1981，39:61－64.

［6］Sun Y G，Meng F W. Note on the paper J Dzurina and I P Stavroulakis［J］. Appl Math Comput，2006，174(2):1634－1641.

［7］Agarwal R P，Grace S R. Oscillation theorems for certain neutral functional-differential equations［J］. Comput Math Appl，1999，38:1－11.

［8］Han Z，Li T，Sun S，et al. Remarks on the paper［Appl Math Comput 207(2009)388－396］［J］. Appl Math Comput，2010，215(11):3998－4007.

［9］Grammatikopoulos M K，Ladas G，Meimaridou A. Oscillation criteria for second-order neutral delay differential equations［J］. Rad Math，1985，1(2):267－274.

［10］Karpuz B，Manojlovic J V，Ocalan O，et al. Oscillation criteria for a class of second-order neutral delay differential equations［J］. Appl Math Comput，2009，210(2):303－312.

［11］Lin X，Tang X H. Oscillation of solutions of neutral differential equations with a superlinear neutral term［J］. Appl Math Letters，2007，20(9):1016－1022.

［12］Liu L，Bai Y. New oscillation criteria for second-order nonlinear neutral delay differential equations［J］. J Comput Appl Math，2009，231(2):657－663.

［13］Meng F，Xu R. Oscillation criteria for certain even-order quasi-linear differential equations with deviating arguments［J］. Appl Math Comput，2007，190(1):458－464.

［14］Xu R，Xia Y. A note on the oscillation of second-order nonlinear neutral functional differential equations［J］. Inter J contem Math Sci，2008，3(29－32):1441－1450.

［15］Xu R，Meng F. New Kamenev-type oscillation criteria for second order neutral nonlinera differential equations［J］. Appl Math Comput，2007，188(2):1364－1370.

［16］Ye L，Xu Z. Oscillation criteria for second order quasilinear neutral delay differential equations［J］. Appl Math Comput，2009，207(2):388－396.

［17］Zafer A. Oscillation criteria for even-order neutral differential equations［J］. Appl Math Letters，1998，11(3):21－25.

［18］Zhang Q，Yan J，Gao L. Oscillation behavior of even-order nonlinear neutral differential equations with varible coefficients［J］. Comput Math Appl，2010，59(1):426－430.