考虑燃油经济性的出行者路径选择模型
2012-06-23冯雨芹冷军强张亚平孙庚冯艳红
冯雨芹,冷军强,张亚平,孙庚,冯艳红
(1.黑龙江工程学院汽车与交通工程学院,黑龙江哈尔滨150050;2.哈尔滨工业大学交通科学与工程学院,黑龙江哈尔滨150090;3.哈尔滨工业大学汽车工程学院,威海264209;4.哈尔滨工业大学 管理学院,黑龙江 哈尔滨150001;5.大连海洋大学信息工程学院,辽宁大连116023)
我国机动车保有量迅猛增长,如何减少交通能耗已成为十分迫切的问题.目前,针对汽车自身节能减排的研究相对比较成熟,而从交通管理角度进行的相关研究却较少.本文拟从交通管理层面,研究燃油消耗因素对出行者路径选择行为的影响,通过燃油消耗与路径选择关系的研究,为出行者提供燃油经济性信息,从而在一定程度上减小出行能耗,达到节能减排之目的.
机动车出行费用通常包括时间费用及燃油消耗费用[1-2].但以往路径选择行为模型,通常仅考虑出行时间相关费用及CO排放量等[3-4],路径选择模型与燃油经济性的关系相关研究较少[5-6].交通诱导系统中提供的路径信息也只有路径长度及行程时间长短等,并没有涉及燃油经济性相关信息.出行费用研究,大多以BPR函数表示的行程时间描述路段的出行费用,以Webster延误公式求取的延误表征交叉口的出行费用[7].
现有出行者路径选择模型主要有随机用户平衡分配模型、弹性需求平衡分配模型等,但这些模型的路阻函数并没有较好地体现出行者在路径选择中的不同需求,如随着人们对能源危机及环境保护的重视,燃油经济性在路径选择中逐步成为考虑因素之一[8].另外,出行需求目标并非单一,往往是多目标且相互矛盾,如更短的行程时间、更高的可靠性、经济性及安全性等.为此,本文在路网单元燃油消耗模型研究的基础上,研究考虑燃油经济性的出行者广义出行费用问题,并研究出行者路径选择行为及费用因素对出行者路径选择行为的影响.
1 考虑燃油经济性的出行者广义出行费用
随着能源危机的加剧及环境保护日趋紧迫,出行者在出行路径选择中,除考虑行程时间、行程时间波动外,越来越考虑和重视燃油经济性问题.降低燃油消耗、减少行程时间、增加可靠性等是出行者的理想目标,但这些目标往往相互矛盾,难以同时得到满足,出行者需要在其所追寻的目标中寻求折中方案.为此,本文以广义出行费用对以上因素进行均衡考虑,将广义出行费用定义为:出行者的燃油消耗量、行程时间及行程时间可靠性的线性加权综合.其中路段、交叉口广义出行费用函数分别表示为

式中:COSTa,COSTnij分别为路段a及交叉口n进口道i中车道组j上的广义出行费用;fa(·)、fnij(·)分别表示路段a及交叉口n进口道i中车道组j的燃油消耗量;Ta、Dnij分别为路段a上的行程时间及交叉口n进口道i中车道组j的车均延误;γ(Ta)、γ(Dnij)分别为路段a行程时间波动及交叉口n进口道i车道组j车均延误的波动;w1、w2、w3分别是燃油消耗、行程时间、行程时间不可靠度在出行者广义出行费用中所占的权重,3个权系数反映了出行者的出行态度,w1越大,则w2和w3越小,即出行者越重视燃油经济性,趋向于以燃油经济性作为路径选择的标准.各个权重可在SP调查基础上确定.
出行者的路径广义出行费用可表示为
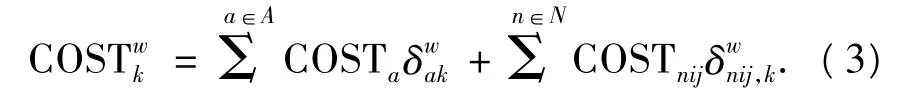
式中:COSTwk为OD对w之间路径k的广义出行费用;为0-1变量,如果OD对w之间的路径k使用路段a,则为 1,否则为 0;为 0-1 变量,如果OD对w之间的路径k使用交叉口n进口道i中车道组 j,则为 1,否则为 0.
1.1 费用指标量化
1.1.1 燃油消耗模型
国内外燃油消耗模型大致可分为如下类别:基于发动机负载油耗模型、基于机动车比功率(VSP)的油耗模型、基于速度或加速度的油耗模型,基于碳平衡原理的油耗模型[9-10].本文利用基于实时路况的车载油耗数据采集系统,分别对哈尔滨市红旗大街及其与长江路交叉口进行了不同交通流状态下的油耗数据采集.以饱和度为参数,利用SPSS进行了回归分析,结果表明:
1)油耗与饱和度的相关性较高,相关系数达到0.92.
2)油耗与饱和度成二次函数关系,可表示为

式中:FC为燃油消耗指标,L/100 km;V/C为饱和度;a、b、c为拟合参数.当饱和度较小,接近于自由流状态时,油耗较高,随着饱和度增加,油耗逐渐减小,当饱和度增至一定值时,油耗又随饱和度一直增加.其原因是当饱和度较小时,驾驶员能够自由选择行驶速度,从而加减速比较频繁,且加减速度比较大,从而油耗增加;但随着饱和度增加,自由行驶机会减少,车辆运行逐渐由自由行驶变为跟驰行驶,加减速行驶工况减少,油耗也随之减小;随着饱和度进一步增加,车流变得较为拥堵,车辆经常处于开开停停状态,且延误也随之大幅增加,即加速、减速、怠速工况比例增加,从而油耗也随之急速增加.
相对路段而言,交叉口燃油消耗指标随饱和度变化更为显著,即饱和度对交叉口燃油经济性影响更为显著.
1.1.2 行程时间与延误
路段行程时间模型研究中最具代表意义的成果是美国联邦公路局(bureau of public roads,BPR)开发的模型,被称之为BPR函数.此模型在交通规划领域影响最大,使用最为广泛,最初只是用于公路网规划之中,后来又被用于城市路网规划.其数学表达式为

式中:Ta为路段a上的行程时间,s;ta为路段a上自由流时的行程时间,s;xa为路段a上的流量,pcu/h;Ca为路段a的通行能力,pcu/h;β,n为模型参数,在国外公路网应用中,其推荐值为β=0.15,n=4.
延误是一个影响因素十分复杂的评价指标,理论计算值难于同实际情况精确吻合.当无条件全面现场调查,如交通规划、交通分配可采用HCM2000延误计算模型进行估算.各车道组延误估算公式为

式中:d1为均匀延误,即车辆按均匀分布到达所产生的延误,s/veh;d2为随机附加延误,即车辆随机到达并引起过饱和排队,分析周期内所产生的附加延误,s/veh;d3为初始排队延误,即分析期初始排队车辆所引起的附加延误,若分析期初始排队车辆数为0,则该值为0.
1.1.3 行程时间或延误波动
1991年Asakura et al[11]提出行程时间可靠性概念来反映行程时间的波动.行程时间可靠性是衡量在规定时间内以一定服务水平完成出行的概率,是衡量行程时间稳定性的指标,反映路网在随机波动交通状态下的应变性能.本文采用的路段行程时间可靠性定义式为

式中:Δ'为可接受的超过自由行程时间的阈值,一般取自由行程时间t的5%、10%、15%、20%等,因为人们对处于不同区位不同路段的交通拥堵容忍程度不同,Δ'应随路段的不同而不同,可以通过SP调查确定;其他参数意义同上.
将式(5)代入式(7)得
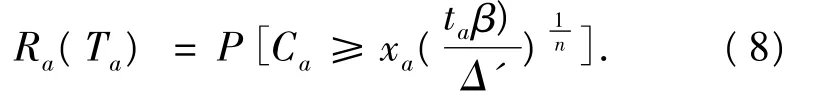
由于路段通行能力Ca随交通流的实际状态变化,为随机变量,其分布函数FCa(x)可通过实地调查拟合得到,则有

式中:r(Ta)表示路段a不满足可靠性要求的概率,也可以理解为出行者在路段a上与行程时间可靠性相关的负效用.
出行者在选择出行路径过程中,对交叉口延误有一个可接受的阈值,由于交通运行的随机性,所以延误时间存在波动,以延误不满足期望阈值的概率来表征延误波动的负效用,计算公式为
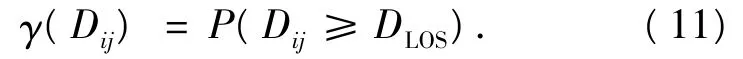
式中:DLOS为出行者在一定服务水平要求下的延误期望阈值,s.
1.2 指标权重确定
指标权重以SP(stated preference survey)调查数据为依据,采用相对比较法确定,首先将所有指标列为方阵,对各指标两两比较打分,打分采用[0,1]打分法,然后对每一指标得分求和,并进行归一化处理.指标i的权重为

式中:aij为指标i相对指标j的重要性.
1.3 指标无量纲化
通过数学变换方法消除广义费用中原始指标量纲的影响,使不同量纲的评价指标具有可比性、可加性.本文拟采用线性比例法进行无量纲化处理,计算公式为:

式中:xi为样本值,yi为xi无量纲化结果,xi'为观测样本值的最小值、最大值或均值.
2 考虑燃油消耗的SUE模型
2.1 模型建立
由于交通状况的复杂性、动态性、随机性,出行者无法完全了解路网中交通流状态,他们对出行路径的选择往往是随机的,因此可用SUE模型来描述出行者的路径选择行为.建立考虑燃油经济性的路径选择模型如下:

2.2 模型算法
3)在新的阻抗基础上,执行一次流量随机加载,得到新的路段流量{yka,∀a};
3 算例
如图1所示测试网络,包括4个节点,5条路段和1个OD对(1→4),OD对流量为2 600 pcu/h,BPR 函数中参数 β=0.15,n=4.节点2、3 采用二相位信号控制,设计通行能力及燃油消耗模型参数如表1所示,算例中Δ'取自由行程时间ta的15%,DLOS按二级服务水平对应的延误阈值选取.以上计算采用Matlab7.0编程处理,其中路网单元可靠性利用Monte Carlo仿真求取.
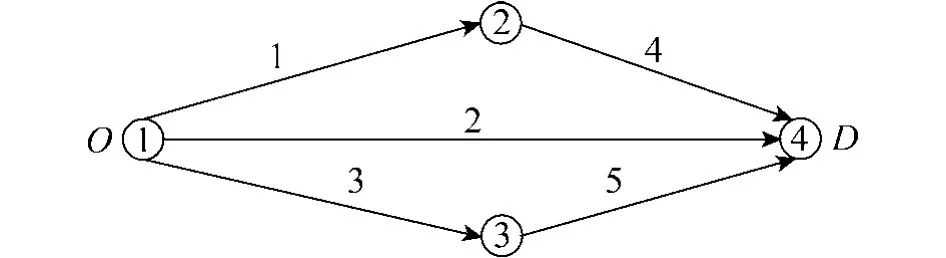
图1 测试路网Fig.1 Test road network
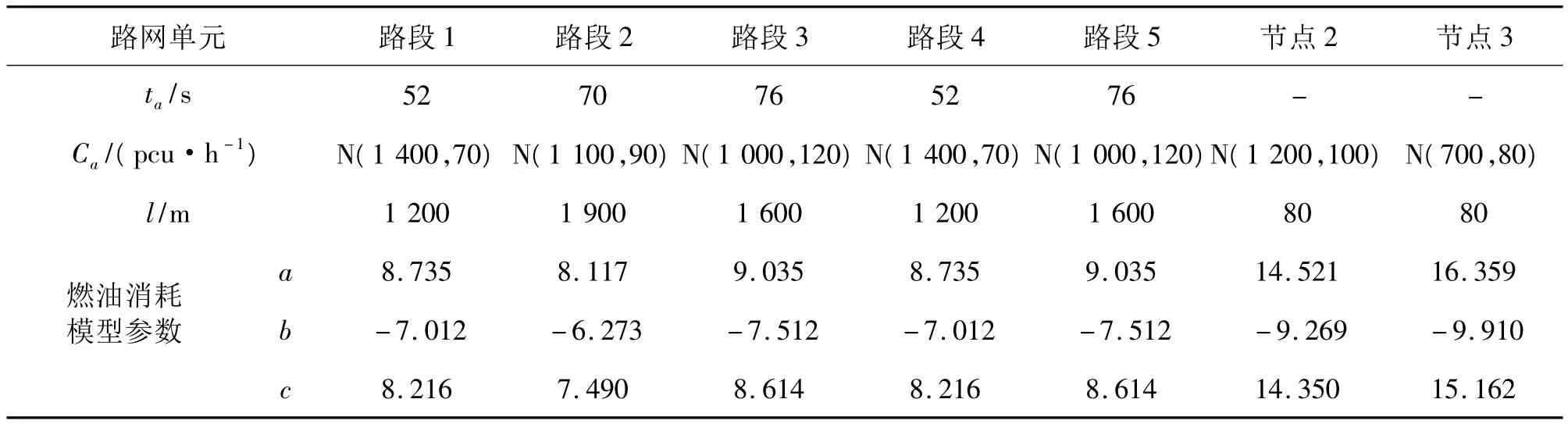
表1 路网单元属性值Table1 Attribute data of road network unit
结果显示:出行者对待出行费用的不同态度对路网交通分配结果有明显影响.从表2中计算结果可看出:当w1逐渐增加直到趋近于1时,即逐渐增加燃油经济性在出行费用中的权重,表示出行者趋向于以燃油经济性为路径选择准则,这时出行者优先选择燃油经济高的路径,由于路段2的燃油经济性最高,故出行者会优先选择该路段,从而该路段所分配交通量逐渐增加,相应燃油经济性差的路段3、5分配交通量明显下降.此时通过计算,整个路网燃油消耗量可减少9.21%.当w2逐渐增大直到趋近于1时,表示出行者趋向于以行程时间为路径选择准则,这时出行者将优先选择行程时间小的路径,从而路段2流量逐渐增加.当w3增大逐渐趋近于1时,表示出行者逐渐趋向于以可靠性为路径选择准则,会优先选择容量大,且波动性小的路径,从而路段1、4分担的流量逐渐增加.

表2 不同费用权重下各路段流量Table 2 Volume under different weight coefficient pcu/h
4 结束语
在路网燃油消耗模型研究的基础上,定义并量化了出行费用各个评价指标,并建立了考虑燃油经济性的随机用户平衡分配模型.通过算例分析了出行者对待燃油经济性不同态度对路径选择有明显影响,考虑燃油经济性的路径选择行为能够明显减少路网燃油消耗总量,算例中路网燃油消耗可减少9.21%,效果明显.本文仅建立了考虑燃油经济性的SUE模型,随着ITS的普及应用,信息化等因素对路径选择行为的影响还需做进一步的研究.
[1]陈建林,刘海旭,程学庆,等.基于行程时间可靠性的多类用户交通分配模型[J].西南交通大学学报,2007,42(1):115-119.CHEN Jianlin,LIU Haixu,CHENG Xueqing,et al.Travel time reliability based traffic assignment model with multiple user classes[J].Journal of Southwest JiaoTong University,2007,42(1):115-119.
[2]赵黎明,王磐.交通网络规划中的出行费用研究[J].河北工业大学学报,2003,32(6):54-59.ZHAO Liming,WANG Pan.The research on travel cost in the traffic network planning[J].Journal of Hebei University of Technology,2003,32(6):54-59.
[3]TZENG G H,CHEN C H.Multi-objective decision-making for traffic assignment[J].Transactions on Engineering Management,1993,40:180-187.
[4]SUGAWARA S,NIEMEIER D A.How much can vehicle emissions be reduced?exploratory analysis of an upper boundary using an emissions-optimized trip assignment[J].Transportation Research Record,2002(1815):29-37.
[5]ERICSSON E,LARSSON H,KARIN B F.Optimizing route choice for lowest fuel consumption-potential effects of a new driver support tool[J].Transportation Research Part C,2006,14(6):369-383.
[6]KYOUNGHO A,HESHAM R.The effects of route choice decisions on vehicle energy consumption and emissions[J].Transportation Research Part D,2008(13):151-167.
[7]LIM Y.Traffic assignment with the turning movements at signal intersection[C]//Proceedings of the 1998 Conference on Traffic and Transportation Studies,ICTTS,Beijing,China,1998:369-378.
[8]BENEDEK C M,RILETT L R.Equitable traffic assignment with environmental cost functions[J].Journal of Transportation Engineering,1998,124:16-22.
[9]SILVA C M,FARIAS T L,CHRISTOPHER F H,et al.E-valuation of numerical models for simulation of real-world hot-stabilized fuel consumption and emissions of gasoline light-duty vehicles[J].Transportation Research Part D,2006(11):377-385.
[10]SMIT R,BROWN A L,CHAN Y C.Do air pollution emissions and fuel consumption models for roadways include the effects of congestion in the roadway traffic flow[J].Environmental Modelling and Software,2008,23(10/11):1262-1270.
[11]ASAKURA Y,KASHIWADANI M.Road network reliability caused by daily fluctuation of traffic flow[C]//Proceedings of the 19th PTRC Summer Annual Meeting,Brighton,England,1991:73-84.
[12]裴玉龙,李宏萍,蒋贤才.城市交通规划[M].北京:中国铁道出版社,2007:122-129.PEI Yulong,LI Hongping,JIANG Xiancai.Urban traffic Planning[M].Beijing:China Railway Publishing House,2007:122-129.
