一种改进的RS编码算法及其FPGA实现

吴晓军，沈向辉，曾志斌

(中国传媒大学广播电视数字化教育部工程研究中心，北京 100024)

一种改进的RS编码算法及其FPGA实现

吴晓军，沈向辉，曾志斌

(中国传媒大学广播电视数字化教育部工程研究中心，北京 100024)

介绍通信系统中广泛应用的RS编码算法，提出了一种改进的伽罗华域的乘法器算法，从而节约了硬件资源的开销，最终通过FPGA平台验证了其可行性和有效性。

RS;伽罗华域乘法器;FPGA

1 引言

RS码(Reed-Solomon Code)是一类具有强纠错能力的多进制BCH码，是目前最有效、用于最广泛的差错控制编码方式之一。相比于其它线性分组码而言，在同样的编码效率下，RS码具有强纠错能力，特别对中等码长，其纠错性能接近于理论值。它既能纠错随机误码又能纠正突发性误码，因此广泛应用于通信、数据存储系统和数字电视传输中。

由于地面广播信道是一个既有随机错又有突发错的混合信道，所以RS码成为首选对象。本文以广泛应用于DVB系统中的RS(204，188)为例介绍其算法原理，并且提出了一种针对RS(204，188)编码中常数项伽罗华域乘法器进行的改进方法，减少了异或门所需个数，从而节省了硬件资源，并最终对改进方案通过FPGA进行实现与验证，测试结果证明了其可行性与有效性。

2 RS编码原理

RS(n，k)码，即RS(n，k，2t)，其由m，n和k三个参数表示，其中m表示码元符号取自域GF(2^m)，n为码字长度(n=2m-1)，k为信息长度，有k个符号。其最多可以纠正t个码元传输错误。编码完成后即在k个信息码元后加了n-k个监督位。如图1所示:RS码的码字多项式、信息多项式和生成多项式分别为:

图1 RS编码框图

RS码的基本思想就是选择一个合适的多项式g(x)(生成多项式)，并且使得对每个信息段计算得到的码字多项式都是g(x)的倍式，即使得码字多项式除以生成多项式所得的余式为0，即:

所以其校验位就是在有限域中经多项式运算最终得到的余数。

3 RS(204，188)编码电路及改进方法

3.1 RS(204，188)编码电路

由式(6)可得RS(204，188)编码电路图，其编码电路为多项式运算取余数的运算过程，如图2所示。

图2 RS(204，188)编码电路图

由于RS(204，188)是RS(255，239)码的截断码，即RS(204，188)其信息段前面加上41个0，即可组成RS(255，239)。即将补零后的239个码元送入编码器，得到16个校验位，输出时再去掉前面的41个为0即可。

对RS(204，188)来说，其生成多项式g(x)与本原多项式p(x)可由Matlab计算得出:

由图2可以看出，此编码电路得到的码字为系统码。信息码元以每k个符号为一组送入编码电路。通过对二选一控制器的控制输出码元，即前k个数据输出为输入数据，数据输入停止，此时通过二选一控制器依次输出移位寄存器的数据即n-k个监督位，最后得到既为n个符号的系统码。

编码电路主要由伽罗华域加法器、伽罗华域乘法器和移位寄存器构成，有限域的加法和乘法运算是编码电路的核心。

3.2 伽罗华域加法器

由伽罗华域的性质可知，伽罗华域加法即为两个加数对应位的模2加，不进位，不错位，只需对相应位做异或运算即可实现(“+”号表示异或运算)。

3.3 伽罗华域乘法器

利用标准基实现乘法器，标准基乘法器不需要基的转换，可以在任何系统中使用，且规则简单，可以很容易地扩展到高阶有限域。要得到A，B在GF域的乘积，先将A，B多项式相乘，然后再将二者的乘积模上本原多项式即可。

假设C表示元素A和元素B相乘的结果，则有:

计算过程和普通多项式的乘法运算一样，因为a为p(x)的根即:

从而依次得出式(11)。

将式(11)代入式(10)得到标准基表示结果，例如C0位为:

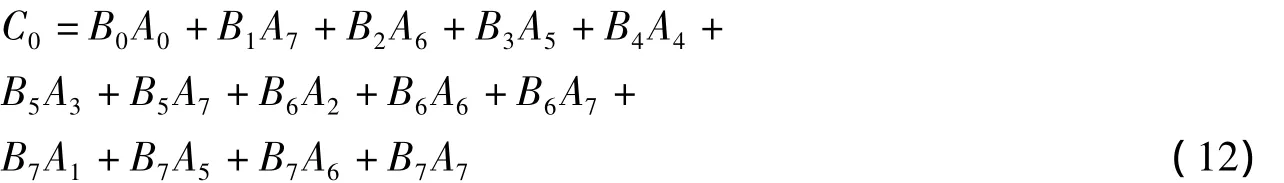
由此得到的是通用的伽罗华域乘法器，由于在RS编码中生成多项式g(x)是已知的，即A(X)是已知的。

因为:1＆E=E，0＆E=0。

则C的表达式可完全由B表示。(如:若A=a225=36，则其二进制表示为00100100)代入c0中可得:

由此类推可得式(14):

由式(14)可知完成该式的乘法运算共需26个异或门。

3.4 一种改进的伽罗华域乘法器

本文提出的方法对文献［7］中方案的改进，文献［7］以a225B为例，其利用逻辑代数的结合律将a225B化简为如下形式:

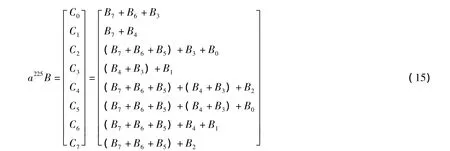
即括号内相同组合项可以先算出，当再次出现时直接利用其计算结果，这样既减少了重复运算又节约了异或门数。

式(15)可改写为:

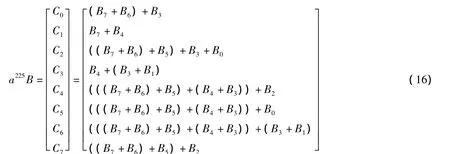
由式(16)可知，输出C的各个比特位ci(i=0…7)所对应的输入B的各比特位具有较多的相同组合项，可以进行进一步的组合。因此以输出C6为例，式(15)中C6表达式为:

改进的式(16)中C6表达式为:

式(16)将式(15)中(B7+B6+B5)写为((B7+B6)+B5)，这样(B7+B6)又可以合并相同项，从而减少异或门数量。

并且为扩大相同组合项的个数，可以适时利用异或门性质(E=E+F+F)，两个F可以分别和其他项进行组合，这样综合考虑加入F+F前与加入后其门数量，选择最少门数方案。

通过优化此a225B共需14个异或门，比优化前节省12个异或门，比文献［7］的优化方法节省2个异或门。

同理可得:

由式(17)可知，此乘法器共需15个异或门比优化前的28个门数节省13个异或门，比文献［7］中节省2个异或门。

由式(18)可知，此项乘法器共需18个异或门比优化前的23个异或门节省5个异或门，比文献［7］中节省1个异或门。

对于其他常数项乘法器可以按照此相同方法得到，由此可见通过优化减少了异或门数量，减少了硬件开销。

4 RS(204，188)编码器改进方案的FPGA仿真与验证

本文采用Altera公司的EP3C16F484C6器件实现了改进后的RS(204，188)编码器，并Verilog HDL代码并导入至Modelim中进行仿真，如图3所示:当编码电路依次输入datain=［1:188］时(1到188的188个等差数列)，可见输出数据dataout在输出188数据后加入了校验位:231 90 194 142 112 85 171 63 242 251 154 1 82 33 222。这与Matlab中运用库函数进行编码输出的结果一致。

图3 RS(204，188)的 Modelim仿真结果

5 结束语

本文简单了介绍了基于DVB系统的编码算法原理，重点分析了RS(204，188)编码电路中最重要的常数项伽罗华域的乘法器设计方法，并提出了一种改进方法。此法与文献［7］中的改进方法相比，更节省了硬件开销，最终通过FPGA平台实现了改进方案，并通过Matlab验证了其正确性。

［1］车晴.电子系统仿真与MATLAB［M］.北京:北京广播学院出版社，2000.

［2］刘昌银.基于对偶基的比特并行算法实现RS编码［J］.北京广播学院学报(自然科学版)，2005，12(1).

［3］Shu Lin，Daniel J Costello Jr.Error Control Coding［M］.北京:机械工程出版社，2007.

［4］曹雪虹，张宗橙.信息论与编码［M］.北京:清华大学出版社，2009.

［5］姜丹.信息论与编码［M］.北京:中国科学技术大学出版社，2009.

［6］刘福奇，刘波.Verilog HDL应用程序设计实例精讲［M］.北京:电子工业出版社，2009.

［7］付兴，樊孝明.一种低复杂度RS编码器的FPGA实现［J］.电视技术，2011，35(9).

［8］陈曦，邱志成，等.基于Verilog HDL的通信系统设计［M］，北京:中国水利水电出版社，2009.

An Improved RS Encoding Algorithm and FPGA Implementation

WU Xiao-jun，SHEN Xiang-hui，ZENG Zhi-bin
(ECDAV，Communication University of China ，Beijing 100024，China)

The RS encoding algorithm widely used in communication system is introduced.And an improved algorithm on Galois Field multiplier is proposed which saves the hardware resources.Finally，its feasibility and validity have been verified through FPGA platform.

RS;galois field;FPGA

TN911.7

A

1673-4793(2012)01-0073-06

2011-12-23

吴晓军(1986-)，男(汉族)，山东人，中国传媒大学硕士研究生.E-mail:wxj0918001@163.com

(责任编辑

:王 谦)