运动基航天飞行模拟器信号缩比策略

陈 炜 姜国华 晁建刚

（中国航天员科研训练中心，北京 100094）

运动基航天飞行模拟器信号缩比策略

陈 炜 姜国华 晁建刚

（中国航天员科研训练中心，北京 100094）

对于大幅值的输入信号，三阶多项式缩比法易产生信号畸变且参数配置复杂;而Hermite缩比函数法的触发速度较慢.提出两种改进的缩比方法:基于三阶多项式缩比法的最优参数配置法和加入线性缩比的非线性缩比法.前一种方法通过参数的优化配置最大化稳定区，以防止信号的畸变;后一种方法则利用线性缩比的特性将缩比度限制在稳定区内.仿真结果表明:线性缩比的加入可以防止三阶多项式缩比法信号的畸变;最优配置参数法应用方便且整体效果较好.为航天飞行模拟提供了更有效的缩比策略.

运动基航天飞行训练模拟器;三阶多项式缩比法;Hermite缩比函数法;最优配置参数法;线性缩比

运动基航天飞行训练模拟器是可以有效且安全地在地面环境下复现真实飞行中航天员行为的系统设备，但其对飞行过程的模拟是有限的.无论是大型的运动基飞行模拟器［1－2］，还是广泛应用的 Stewart平台运动基模拟器［3－6］，由于其运行轨道或平台作动器的尺寸限制，运动空间都只能保持在一定的范围内.例如通用的大中型Stewart平台运动模拟器的平移范围大多在1～2 m之间，可实现的旋转运动在30°左右.所以运动基模拟器不可能对真实的飞行过程进行等幅值的模拟，而是需要对飞行线加速度和角速度等信号的幅值进行一定程度的缩放，建立一个实际飞行过程的缩比模型，使其运动幅值限制在模拟器的运动空间之内，同时保持人体对运动感知所需的关键部分.实际工程应用中运动空间限制的实现方法有两种:一种是在信号洗出前对输入信号进行缩比处理，另一种则是对模拟器作动器的伸缩量进行限制.后一种方法可以很好地保护模拟器不使其超出运动空间，但这种相对保守的方法限制了洗出算法的参数优化配置，常常会导致严重的运动提示错误［6］.所以在多数情况下，希望可以通过对输入信号进行适当且安全的缩比处理，释放作动器方面对运动空间过于生硬的保护，以使洗出算法充分地发挥效用，进而提供准确而真实的飞行模拟.

本文从工程应用及缩比效果出发，分析了两种缩比法的特点及其在航天飞行模拟中存在的不足;针对不足，分别提出了基于三阶多项式缩比法的最优参数配置和线性与非线性缩比法结合的策略.仿真结果表明，线性缩比的加入可以防止三阶多项式缩比法信号的畸变;最优配置参数法应用方便且可使触发速度与峰值波形均达到理想效果.

1 缩比方法简介

运动基模拟器主要处理的是线加速度和角速度信号.为了充分利用人体的感知特性，要求信号缩比具有幅值响应，即对于输入信号不同的幅值段具有不同缩放比例，其基本原则为:对于触发段的信号，希望它相对的大，以使人及时感觉到运动的变化，减小感觉延时;对于峰值段的信号，则需要对其进行较大的缩放，将其限制在模拟器可实现的范围内.这也是缩比效果主要的判别标准.

信号缩比的方法总的可分为两种:线性缩比法和非线性缩比法.线性缩比法会产生明显的不连续点且无法实现幅值响应，在应用中通常采用非线性缩比法.

非线性缩比法在保证整个区域信号连续性同时，对不同幅值段的信号实现了不同幅度的缩放比例.三阶多项式缩比法（简称“三阶缩比法”）是应用最广的非线性缩比方法，如NASA兰利研究中心的视觉运动模拟器就使用这种方法［3，7］，但它的参数确定较复杂，导致模拟器的参数优化困难.同时，由于三阶缩比法并没有对局部极值点进行限制，当信号在较大幅值范围内单调增大或减少时，容易使输出信号陷入局部极值而导致信号畸变.Hermite缩比函数法来自于Hermite插值多项式［8］，2007 年，文献［9］初次提出可以将其应用于模拟器输入信号的缩比处理中.Hermite缩比法的参数确定方便且预防了局部极值点的出现，但牺牲了触发速度，会导致运动感知的延时.表1为以上两种缩比方法的对比.

表1 缩比方法对比

相对于地面飞行，航天飞行中常常会经历线加速度或角速度运动在较大幅值范围内的持续增大或减小，典型的如返回再入段的过载在0到超过3g（g=9.8 m/s2）范围内持续增加和减小的变化过程，而故障情况下采用的弹道式返回过载的变化可能达到、甚至超过10g.此时，对于运动基航天飞行训练模拟器，三阶缩比法不能满足要求;而Hermite缩比函数法又不适用于对触发速度要求较高的场合.本文针对上述两种方法的不足，并依据航天飞行模拟的特点，提出两种改进策略.

2 两种缩比方法的基本理论

2.1 三阶多项式缩比法

假设x为输入信号，y为输出信号，利用一个三阶多项式来描述两者的关系:

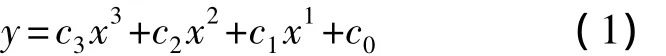
其中，xm是预期的最大输入;ym是对应的最大输出;λ0和λ1分别是x=0和x=xm时的变化率（导数值）.三阶多项式缩比法系数的确定需要已知上述4个参数.

2.2 Hermite缩比函数法

Hermite缩比函数法（简称“Hermite缩比法”）是通过控制输入信号和对应输出间的缩比值来实现的，即

其中s（x）称为缩比函数，满足:

其中，h1（x），h2（x），h3（x），h4（x）为4种基本的三阶Hermite差值多项式，分别为

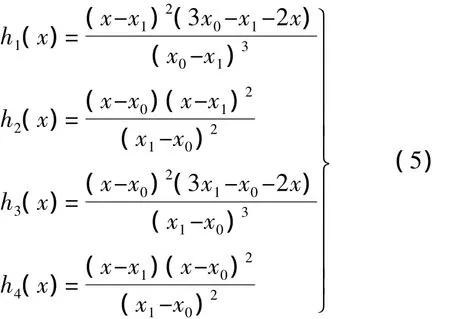
其中，x0为最小输入值，一般取0;x1为最大输入值（同xm）;s0和s1分别为x0和x1处对应的缩比值;d0和d1为缩比函数s（x）在x0和x1处对应的斜率.输入与输出间的函数关系为

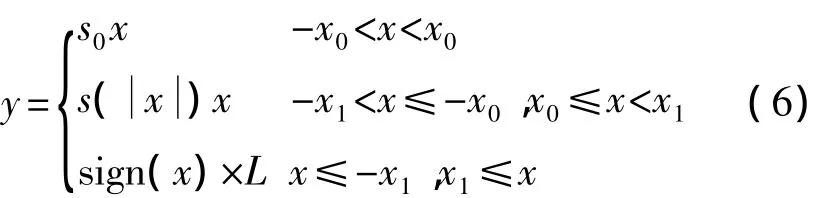
其中，L称为最大输出值或输出阈值（同xm），且y（x1）=s1x1=L.

由于Hermite缩比函数法分离出了缩比函数s（x），所以可以通过控制s（x）的相关特性方便地实现所需的缩比效果.其遵守以下3个条件:

1）d0=s'（x0）=0.

2）当 x∈［x0，x1］，s（x）＞0.

3）当 x∈［x0，x1］，s'（x）≤0，说明触发段的信号缩放比例较大，而峰值段的缩放比例较小.

同时为了防止局部极值点的出现，Hermite缩比函数法加入了下面2个条件:

4）当 x∈［x0，x1］，y'（x）≥0 且 y'（x1）=0，保证了输入与输出信号的单调性一致.

5）y″（x1）=0，防止在预期最大输入点x1附近出现局部极值.

综合以上5个条件，可以得到下面关系式:

依据上式，Hermite缩比函数法只需已知参数s0，s1，x1和L中的任意两个就可以确定s（x）的系数.通常x1及L为已知量，由其可以方便地获得满足条件的Hermite缩比函数.

3 基于三阶缩比法的最优参数配置

3.1 缩 比 度

为了分析航天飞行模拟中输入信号幅值范围对单调信号缩比效果的影响，本文引入参数C（输入信号最大幅值与输出阈值间的比值）描述信号的缩比度，并以C值为变量讨论其对缩比效果的影响.对于三阶缩比法:C=xm/ym;Hermite缩比法:C=x1/L.图1所示为两种缩比法在不同缩比度时的缩比效果比较.其中λ0和λ1分别为1和0.1，输出阈值 ym（即 L）为 10.

图1 缩比度对缩比效果的影响

从图1中可以看出，对于三阶缩比法，随着C值的增加输出信号的畸变越来越严重，但触发段表现稳定;Hermite缩比法中输出信号的单调性则并没有受到缩比度变化的影响，但是其触发段的速度随着缩比度的增大而减小.

3.2 稳 定 区

从图1a可以推断，对于给定的参数，三阶缩比法存在一个稳定区，当缩比度在此区域内时，可以保证输入-输出曲线不出现局部极值，避免信号的畸变;而缩比度越远离，信号越不稳定.为此有下面的证明.

证明 对式（1）求导，可得

由于 λ0≥λ1≥0，根据式（2）有 c1＞0，c2＜0 且c3＞0.根据二次函数理论，y'（x）≥0成立的情况只有两种:

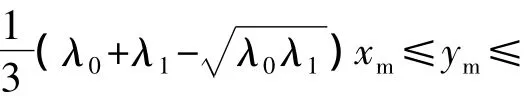
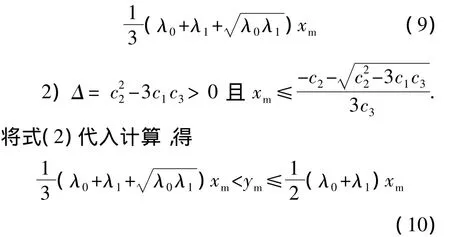
综合上述两种情况，可得

将C=xm/ym代入式（11），得

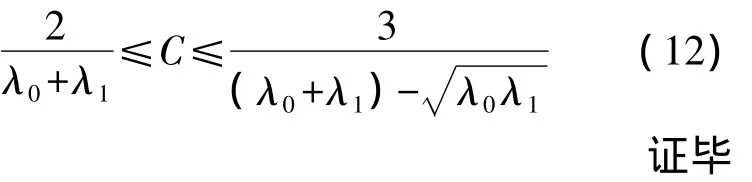
同时易证:当式（12）成立时有 y″（x）≤0，即触发段的信号缩放比例较大，而峰值段的信号缩放比例较小，此处不再赘言.实际缩比应用中通常C=xm/ym≥1，式（12）取为

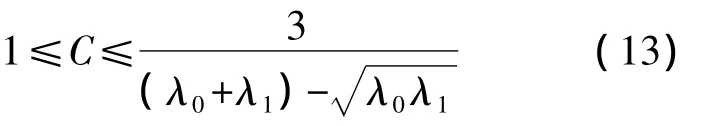
3.3 最优参数配置法

三阶多项式缩比法参数配置的难点在λ0和λ1.输出信号触发段的效果主要由λ0决定，λ1则主要影响峰值段的波形，同时式（13）表明它们的取值也决定着稳定区的范围.下面首先分析λ0和λ1与稳定区上限的关系.稳定区的上限为

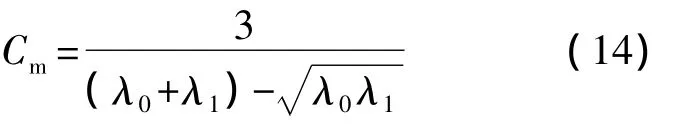
图2 所示为 λ0分别为 0.5，1，2 时，缩比度上限Cm随λ1变化的曲线，图中所标点为相应曲线的最值点.

图2 Cm随λ0和λ1变化的曲线

从图2中可以推断:当λ0一定时，Cm由λ1决定，且存在最值点.对式（14）进行最值分析，可得

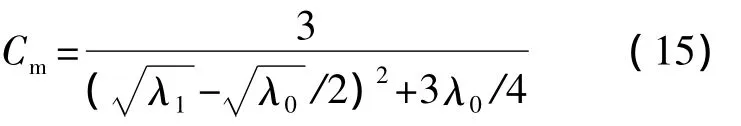
即当 λ1=λ0/4 时，Cm取得最大值 4/λ0.λ0和 λ1为对偶关系，由于λ0≥λ1≥0，忽略另一种情况.

在实际缩比应用中，对于一个模拟任务，其缩比度C已定，则可根据最值点来配置λ0和λ1为

此时，既可使缩比度处在稳定区，也可使稳定区的范围最大.

4 线性缩比与非线性缩比的结合

4.1 三阶缩比法与线性缩比结合

对于三阶缩比法缩比度超出稳定区的情况，另一种方法是在非线性缩比之前进行线性缩比.与最优参数配置不同，此方法是通过调整缩比度来适应所配置的参数.线性缩比可以对缩比度进行直接调整，将其限制在稳定区内.

设线性缩比因子为K，原缩比度为C，线性缩比后为CL，则两者关系为

当参数确定后，三阶缩比法的缩比度稳定区就确定了.为了使线性缩比后缩比度处于稳定区内，需要满足:

此时，线性缩比因子K要满足:

由于线性缩比不具有幅值响应特性，对触发端与峰值段进行了相同的缩放.此时为了使峰值段满足条件，势必导致触发速度等比例减小.所以为了减弱这种影响，通常线性缩比因子取为满足式（8）时的最小值，即

4.2 Hermite缩比法与线性缩比结合

Hermite缩比法本身已经进行了参数的最优配置，下面分析线性缩比对Hermite缩比法的影响.设xL为线性缩比后的信号，且有xL=x/K，相应的有:

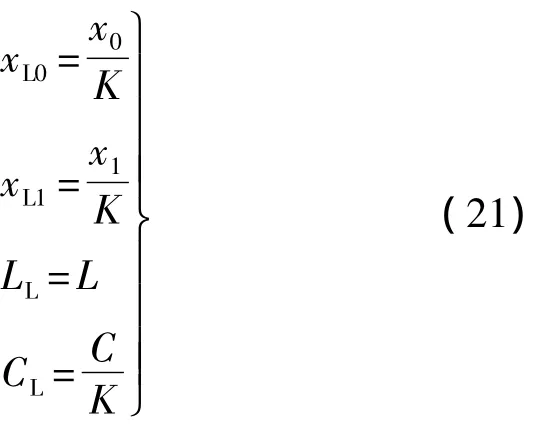
将式（21）代入式（5）可得

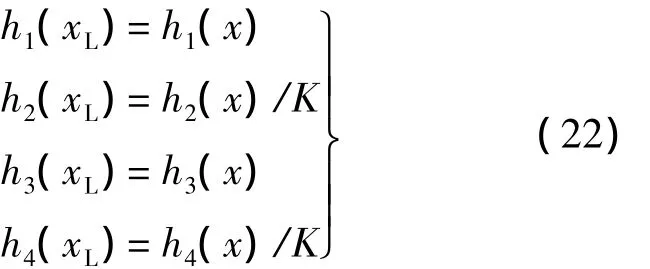
将式（21）代入式（7）可得

将式（22）与式（23）代入式（4）可得

则有

式（25）说明了线性缩比对Hermite缩比法并不产生效用.当输出阈值L一定，缩比函数s（x）随输入信号x变化区间的压缩而等比例扩大，保持了输出信号y的不变性.

5 仿真比较和分析

以航天器返回再入段纵向加速度a（m/s2）为输入信号，使用Matlab进行算法仿真，原始数据参照俄罗斯联盟号系列飞船，如图3所示.运动基模拟器性能标准采用NASA兰利研究中心的视觉运动模拟器［8］，纵向加速度输出阈值设为7 m/s2.根据输入信号与模拟器性能配置三阶缩比法与Hermite缩比法的参数，如表2所示.

图3 输入信号

表2 参数设置

5.1 加入线性缩比

将表2中λ0和λ1值代入式（14）可得Cm=3.8，代入式（19）可得线性缩比因子K的范围为

如图4所示分别为K=4和1.49时三阶缩比法与Hermite缩比法未加和加入线性缩比的缩比效果对比.

由于C＞Cm，图4a中三阶缩比法峰值段的输出信号发生畸变，超出了阈值;而Hermite缩比法未加与加入线性缩比的输出信号完全重合，证明了线性缩比对Hermite缩比法没有效用;加入线性缩比后的三阶缩比法，输出信号保持在阈值范围内，峰值段的波形得到了很好的改善，但此时触发速度要慢于三阶缩比法与Hermite缩比法.图4b中的线性缩比因子满足式（20），此时加入线性缩比的三阶缩比法的触发速度处于Hermite缩比法与三阶缩比法之间;峰值段的波形接近Hermite缩比法.图中加速度感知阈值为0.07 m/s2.

5.2 最优参数配置法

将 C=5.7 代入式（16），可得

即为最优参数配置的三阶缩比法，分别与Hermite缩比法及加入线性缩比的三阶缩比法（K=1.49）进行比较，如图5所示.

在峰值段，最优参数配置法（图中“最优三阶”）的波形更如实地反应了信号的变化趋势;最优参数配置法的触发速度与加入线性缩比的三阶缩比法相近，同样优于Hermite缩比法.

5.3 缩比策略

通过以上的仿真比较，可以得出以下几个结论:

1）三阶最优参数配置法与加入线性缩比的三阶缩比法的触发速度都较快，同时均克服了信号畸变的问题，保证了信号的单调性.对于缩比度大于其上限的情况，即C＞Cm，相对于三阶缩比法，他们均可以有效抑制信号畸变，防止输出信号超出阈值;相对Hermite缩比法，两种方法则均可以实现更快的触发速度.

2）同Hermite缩比法一样，三阶最优参数配置法不需要进行人工的参数配置，只需通过缩比度来配置最优的参数值;加入线性缩比的三阶缩比法则需要提前给定λ0和λ1值，并以此来计算所需的线性缩比因子，所以它适合要求实现特定λ0和λ1值的缩比处理.

图4 线性缩比因子K=4与1.49时几种缩比法的比较

图5 最优参数配置的三阶缩比法与两种缩比法的比较

6 结论

本文对两种缩比法进行了分析与改进，提出了最优参数配置的三阶缩比法、线性缩比与非线性缩比法结合的两种缩比策略.从触发速度与峰值段波形两个标准出发，同时考虑工程应用难易，对各种缩比方法进行仿真比较.对于C＞Cm的情况，加入线性缩比的三阶缩比法防止了输出信号的畸变;最优参数配置的三阶缩比法则可以得到较好的整体效果.本文最后总结了两种缩比法的特点，并给出了缩比策略.实际应用中需要考虑输入信号的特点以及所需的关键信息，选择最适合的缩比方法.

（References）

［1］Aponso B L，Tran D T，Schroeder J A.Rotorcraft research at the NASA vertical motion simulator［R］.AIAA-6056，2009

［2］BlesW，GroenE.TheDESDEMONA motionfacility:applications for space research ［J］.Microgravity Science and Technology，2009，21（4）:281－286

［3］Telban R J，Cardullo F M.Motion cueing algorithm development:human-centred linear and nonlinear approaches［R］.CR-2005-213747，2005

［4］Berkouwer W R，Stroosma O.Measuring the performance of the SIMONA research simulator's motion system［R］.AIAA-2005-6504，2005

［5］Zhou Y F，Ji X C，Li H L，et al.Structural design and the state of motion analyzes for multi-degree-of-freedom electro-hydraulic mix-drive motion simulator［J］.Key Engineering Materials，2010（419/420）:169－172

［6］田浩，赵阳，张大伟.对接机构综合试验台运动模拟器建模分析［J］.宇航学报，2007，28（4）:996－1001

Tian Hao，ZhaoYang，ZhangDawei.Movementsimulator modeling and simulation in integrate test platform for docking mechanism［J］.Journal of Astronautics，2007，28（4）:996 －1001（in Chinese）

［7］Telban R J，Cardullo F M，Kelly L C.Motion cueing algorithm development:piloted performance testing ofthe cueing algorithms［R］.CR-2005-213748，2005

［8］Kincaid D，Cheney W.数值分析［M］.王国荣，俞耀明，徐兆亮，等译.北京:机械工业出版社，2005:268－275

Kincaid D，Cheney W.Numerical analysis［M］.Translated by Wang Guorong，Yu Yaoming，Xu Zhaoliang，et al.Beijing:Machine Press，2005:268－275（in Chinese）

［9］Schwarz C W.Two mitigation strategies for motion system limits in driving and flight simulators［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part A:Systems and Humans，2007，37（4）:562－568

Signal scaling strategies for motion-base spaceflight simulators

Chen Wei Jiang Guohua Chao Jiangang
（China Astronaut Research and Training Center，Beijing 100094，China）

When input signal is scaled in a large scope，the third-degree polynomial scaling is easy to induce signal distortion and complicated for parameters tuning，and the trigger speed of Hermite scaling is too slow to satisfy the condition.Based on this situation，two methods were put forward:the scaling of optimal parameter configuration based on the third-degree polynomial scaling and the non-linear scaling combined with linear scaling.The first method maximizes the stable region to prevent signal distortion by optimizing the configuration parameters;the latter one restricts the scaling scope in the stable region by utilizing the characteristics of linear scaling.The results have indicated that signal distortion can be avoided when the linear scaling joins in the third-degree polynomial scaling，and the method based on optimal parameter configuration shows advantages in parameters tuning and integrated scaling performance.The two methods provide more effective scaling strategies for spaceflight simulation.

motion-base spaceflight training simulator;third-degree polynomial scaling method;Hermite scaling method;scaling of optimal parameter configuration;linear scaling

V 211.73;TP 391.9

A

1001-5965（2012）03-0324-06

2010-11-30;< class="emphasis_bold">网络出版时间:

时间:2012-03-20 10:37

www.cnki.net/kcms/detail/11.2625.V.20120320.1037.004.html

陈 炜（1983－），男，陕西宝鸡人，硕士生，chenweii521@sina.com.

（编 辑:李 晶）