基于跟踪微分器的多目标数据关联算法

李 勇 霍 伟

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

多目标跟踪问题无论在军事和民用方面都有着十分广泛的应用，如弹道导弹防御、空防、空中打击、海洋监视、战场监视以及空中交通管制等等.因此，这一问题一直是多年来研究的热点.多目标跟踪过程的关键是如何进行有效的数据关联，数据关联是多目标跟踪技术中最重要而又最困难的方面.传统的数据关联技术有很多，如最近邻(NN，Nearest Neighbor)［1］、联合概率数据关联(JPDA，Joint Probabilistic Data Association)［2］、多假设跟踪(MHT，Multiple Hypothesis Tracking)［3］等.MHT考虑回波来源与目标、杂波和新目标等各种可能的情况，构造面向量测的关联假设数，以实现多目标的数据关联和跟踪.JPDA是MHT方法的一个特例，避免了NN算法唯一性可能造成的关联出错.JPDA一直是公认的精度较好的经典数据关联方法，但其计算量随着目标和回波数增长呈指数递增，往往难以满足实时性要求.不少学者根据实际问题不断提出JPDA的一些改进算法，如文献［4－6］等.这些改进算法都是在JPDA可行性规则的基础上进行某种假设，以牺牲精度为代价，未从根本上解决JPDA的计算量问题.

上述这些算法多基于概率统计方法，往往需要假设量测噪声、杂波服从某种统计规律，且关联算法与滤波跟踪算法耦合，滤波跟踪算法的精度直接影响数据关联的准确性.针对这些问题，本文用不依赖于模型的跟踪微分器(TD，Tracking Differentiator)来实现杂波环境下的数据关联，在降低对计算能力要求的同时还可以避免因为目标模型或噪声等统计规律可能与实际情况不符合带来的误差.

1 基于TD的多目标数据关联

所谓TD是这样的机构:对它输入一个信号，它将输出两个信号，其中一个信号跟踪输入信号，而另一信号可近似为跟踪信号的微分.TD因为其优秀的品质，在很多领域得到了广泛的应用［7］.考虑到信号跟踪的快速性和滤波要求，文献［8］提出了如下形式的TD，并证明了其全局收敛性:

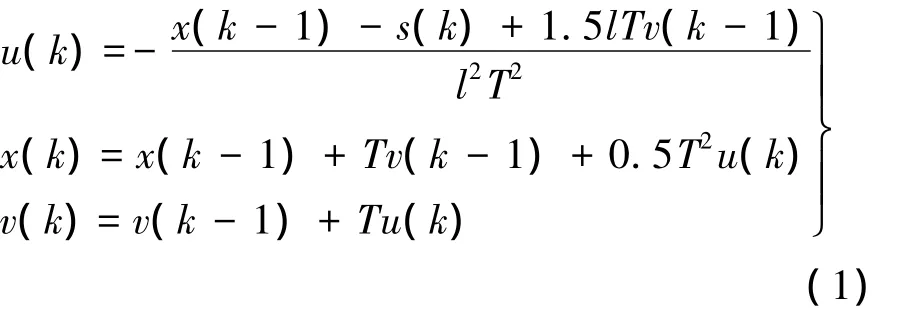
式中，x(k)和 v(k)为 k时刻系统的输出信号;u(k)为该时刻控制量;s(k)为输入信号;T为采样周期;l为滤波因子.

在将式(1)用于目标跟踪时，当输入的信号s为目标位置时，则输出x跟踪目标的位置，而v为目标的速度.

1.1 关联算法的基本思路

本文提出的算法先利用TD构造波门，然后用TD处理波门内所有量测.将TD得到的量测的位置和速度与目标前一时刻的位置和速度进行比较，用同时满足位置和速度差最小作为第1关联条件，将波门内符合第1关联条件的量测与已知目标关联;若所有量测均不满足第1关联条件，则用当前TD得到的量测的位置和速度回推出上一时刻的目标位置，将此位置与目标前一时刻位置的距离差最小作为第2关联条件，将满足第2关联条件的量测与已知目标关联.当一个循环周期所有目标关联完毕后，若出现某量测同时关联两个以上目标，首先用关联条件的优先级来确定是否将该量测与目标关联;当用关联条件优先级不能排除量测被同时关联时，则将相应目标关联条件中的次小值列为备选关联量测.通过比较各次小值和上述最小值与相应目标预测位置的距离来确定将次小值还是最小值与该目标关联.经上述步骤处理后，若出现某次小值被同时关联的情况，则将关联条件中的第3小值列为候选关联量测，用类似方法处理，直至所有目标被一一关联.

1.2 关联算法的基本步骤

下面以二维平面内的目标关联为例说明基于TD的多目标数据关联算法的具体步骤.对于三维空间目标，只需要增加与立轴对应的一组TD，关联方法与平面目标相同.

为简化问题，提出如下基本假设［9］:

1)目标数及初始状态已知;

2)每一量测有唯一的源，即任一量测不源于某个目标，则必然源于杂波或虚警;

3)对于一个给定的目标，最多有一个量测以其为源.如果一个目标产生多个量测，将取一个为真，其它为假.

基于TD的数据关联算法具体步骤如下:

1)形成跟踪波门.

根据假设1)对与n个目标对应的TD用两点差分法［9］初始化.当处理中心接收到量测值，为减少计算量和杂波干扰，在目标状态的预测位置附近区域形成波门，波门大小依据目标最大机动能力确定(当对目标机动无先验知识时，可放宽波门的设置门限).

若已知第i个目标在k－1时刻用TD关联算法处理后得到的位置和速度分别为(xi(k－1)，yi(k－1))和(vxi(k－1)，vyi(k－1))，则第 i个目标k时刻的波门为

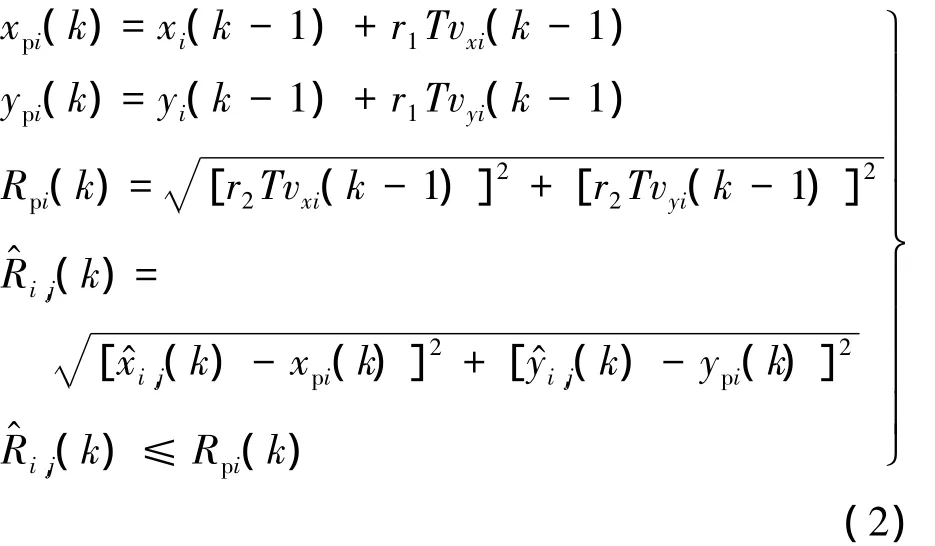
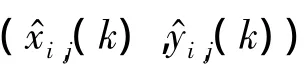
2)单个目标量测的TD处理.

设k时刻落入第i个目标TD波门内有z个量测(x^i，j(k)，y^i，j(k))，j=1，2，…，z.将这 z个量测序贯送入第i个目标的一对TD处理后得到z个与目标对应量测的位置(xi，j(k)，yi，j(k))和速度(vxi，j(k)，vyi，j(k)).

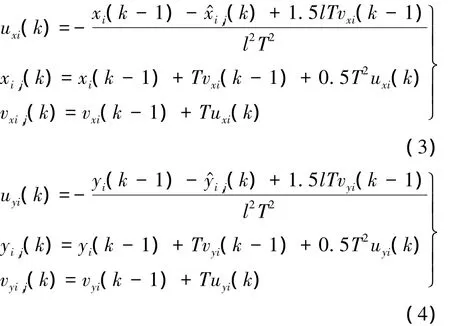
将TD得到的k时刻第i个目标量测的位置和速度与其在k－1时刻的位置和速度分别进行比较，即

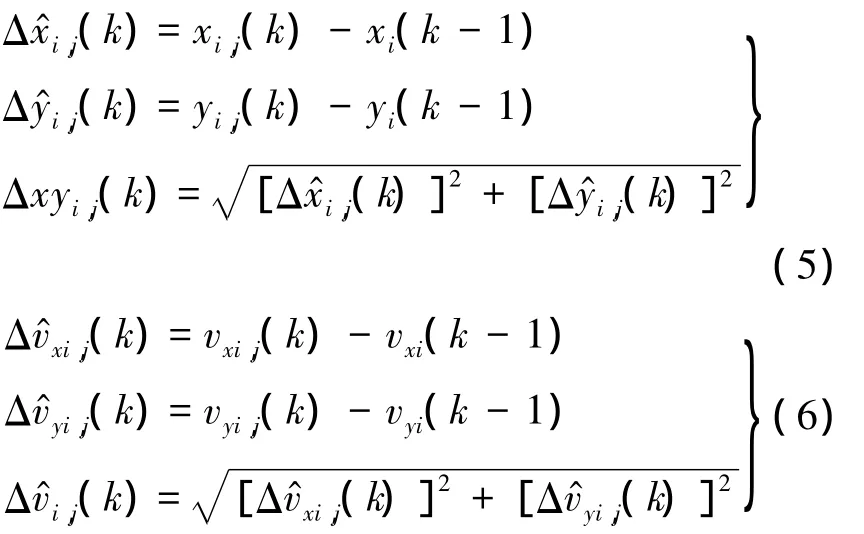
对这z个位置差和速度差求最小值，分别为

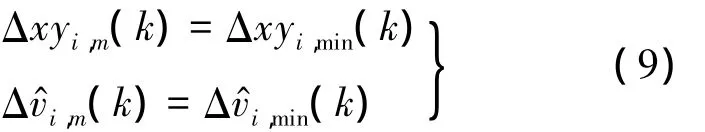
则将此量测与目标i关联.

式(9)称为第1关联条件.这一关联条件的依据是:目标从k－1时刻经1个采样周期后其位置和速度均不应发生突变.

如无同时满足第1关联条件的量测存在，则需要计算:

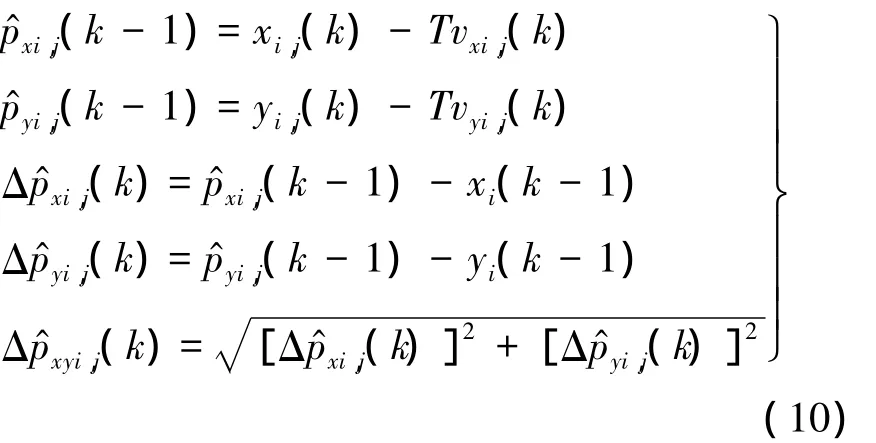
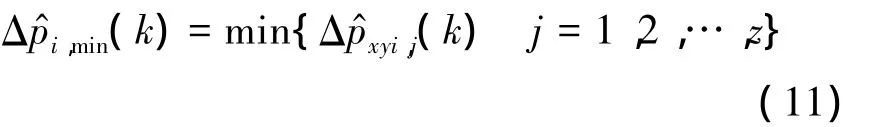
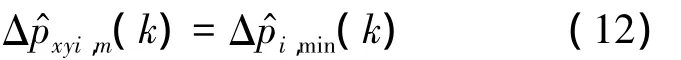
则将此量测与目标i关联.

式(12)称为第2关联条件.该关联条件反映了目标 k时刻的位置不应从 k－1时刻经突变得到.

落入其余n－1个目标对应TD波门的量测用上述方法并行处理.

3)多目标TD数据关联.

①目标TD波门内无量测视为漏检;

②目标TD波门内有1个量测，则将此量测与目标关联并用TD处理;

③目标TD波门内有2个以上量测，用关联条件将量测与目标一一关联;

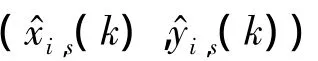
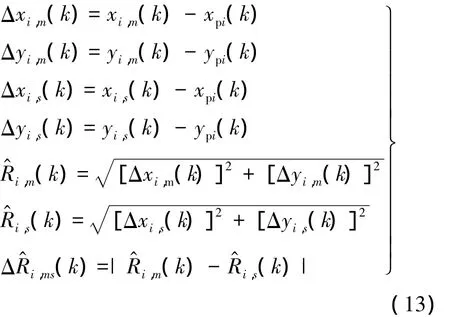
则将此量测与目标i关联，而将其余的ns－1个目标对应的次小值量测与相应目标关联.

式(13)～式(15)的处理方法称为次小值处理法.其依据是:当不能用最小值确定关联关系时，可取次小值为备选关联量测.计算出次小值和该最小值分别与目标预测位置的距离，最大距离对应的次小值予以排除，同时由假设3)所述目标关联的唯一性知:应将最小值与该次小值对应的目标关联，其他次小值与各自目标预关联.若有次小值不能被唯一关联，重复使用次小值处理法直至所有目标被一一关联.

1.3 关联算法的计算复杂度

表1列出了MHT和各种常用JPDA算法以及TD算法的计算时间复杂度，m为波门内回波数，n为目标数，从表中可以看出TD关联算法的计算复杂度最小.

表1 算法时间复杂度比较

1.4 错误关联率分析

如图1所示，p点和q点分别为目标i在k及k+1时刻的位置;abcd点为传感器测量值的最大偏差位置;若x与y方向的测量偏差为σx和σy，则正方形的面积为4σxσy.ef点为线段pd和线段pa与波门边界的交点.

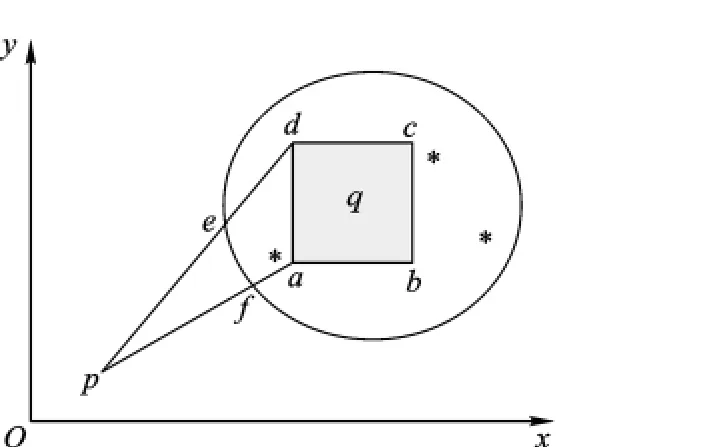
图1 错误关联率示意图

根据TD关联算法，落在由点abcdef围成的几何空间内的杂波点都有可能被错误关联.设此图形面积为S，落入波门的杂波数为c，则最大错误关联概率为

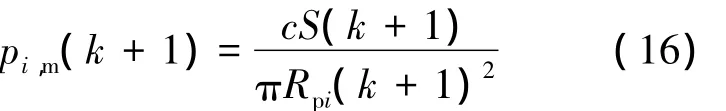
由式(16)可以看出:当波门面积一定时，算法最大错误关联概率与波门内杂波数以及传感器测量误差相关，杂波数越多，测量误差越大，算法错误关联率越高.

2 仿真实验

本例利用文献［9］数据进行算法仿真，并与常用的几种算法进行正确关联率比较以检验提出算法的可行性.

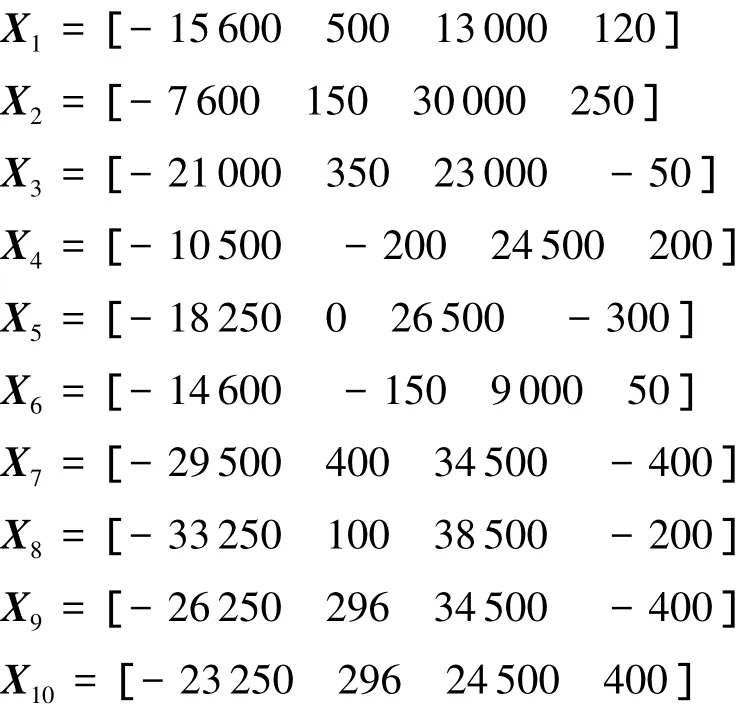
在传感器测距误差σr=100 m，测角误差σθ=0.01 rad，采样间隔T=1 s，不同杂波密度，目标匀速运动条件下得到所需仿真数据.图2为单位面积杂波数λ=10×10－6的仿真结果.图3为算法正确关联率比较，其他算法结果出自文献［9］.

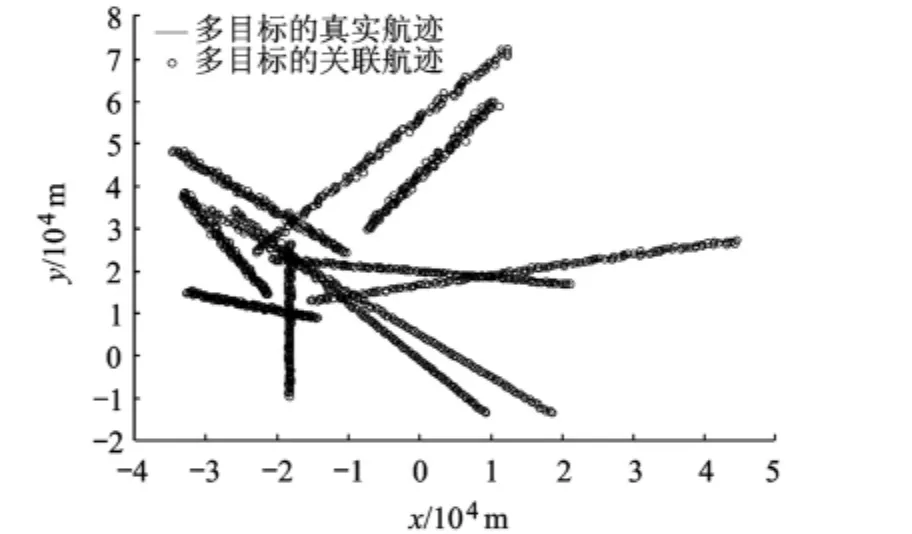
图2 TD关联算法仿真结果

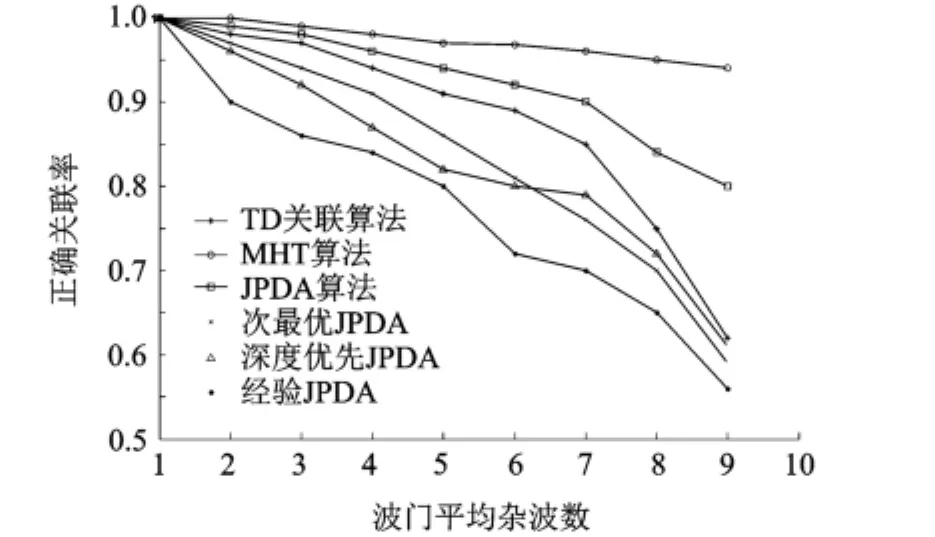
图3 算法正确关联率随平均杂波数变化图

通过图3及表1算法计算复杂度比较，MHT算法在目标较为密集的情况下正确关联率最高，但算法的计算复杂度最大;JPDA算法的正确关联率低于MHT算法但高于各种简化的JPDA算法，但该算法的计算复杂度仅次于MHT算法;在3种简化的JPDA算法中深度优先搜索法在杂波数小于4的时候正确关联率好于其他两种;次最优JPDA算法在杂波数小于4时算法正确关联率稍差于深度优先算法而在杂波数大于4时正确关联率好于其他两种算法;经验JPDA算法正确关联率差于其他两种算法.

仿真结果表明:TD关联算法正确关联率低于MHT算法和JPDA算法，但其计算复杂度小于这两种算法;在杂波数小于7的时候正确关联率好于3种简化的JPDA算法，杂波数在8和9时其正确关联率与深度优先和次最优JPDA算法相当，杂波数在大于8后其正确关联率下降较快，不适于杂波较为密集的环境.

3 结论

本文利用跟踪微分器的跟踪特性，提出了一种新的未知杂波环境下多目标跟踪关联算法.此算法计算量小，实时性强，易于工程实现.仿真结果表明算法在杂波不很密集的情况下对多目标具有良好的关联能力.下一步将考虑如何利用跟踪微分器来实现目标数未知时的数据关联.

References)

［1］Ruan Y，Hong L.Analytic performance prediction of feature aided global nearest neighbor algorithm in dense target scenarios［J］.Radar，Sonar and Navigation，2007，2(5):369－376

［2］Blom H A P，Bloem E A.Probabilistic data association avoiding track coalescence［J］.IEEE Transactions on Automatic Control，2000，45(2):247－259

［3］Obata Y，Ito M，Kameda H.Tracking algorithm using N-back scan MHT under dense environment［C］//2008 SCIE Annual Conference.Tokyo:IEEE Press，2008:3436－3440

［4］Puranik S，Tugnait J K.Tracking of multiple maneuvering targets using multiscan JPDA and IMM filtering［J］.IEEE Transactions on Aerospace and Electronic System，2007，43(1):23－35

［5］Aoki E H，kienitz K H.Suboptimal JPDA for tracking in the presence ofclutter and missed detections［C］//IEEE Proceedings of the 12thConference on Information Fusion.Seattle WA:IEEE Press，2009:818－825

［6］Shi Zhangsong，Xiao Sheng.An improved data association algorithm for multiple-target tracking［C］//2010 International Conference on Computational and Informational Sciences.Chengdu:IEEE Press，2010:553－556

［7］韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008:46－97

Han Jingqing.Active disturbance rejection control technique［M］.Beijing:National Defense Industry Press，2008:46－97(in Chinese)

［8］Li Yong.A complementary form of discrete tracking differentiator［C］//2010 International Conference on Measuring Technology and Mechatronics Automation.Changsha:IEEE Press，2010:46－49

［9］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京:电子工业出版社，2006

He You，XiuJianjuan，Zhang Jingwei，etal.Radardata processing with applications［M］.Beijing:Publishing House of Electronics Industry，2006(in Chinese)