用于GMA的新型永磁偏置闭合磁路

杨远飞 张天丽 蒋成保

(北京航空航天大学 材料科学与工程学院，北京100191)

超磁致伸缩材料(GMM，Giant Magnetostrictive Material)相比于压电材料、形状记忆合金、电致伸缩材料等其它智能材料而言，具有响应速度快、工作频带宽、驱动电压低等优点，所以利用磁致伸缩材料研制的超磁致伸缩执行器(GMA，Giant Magnetostrictive Actuator)在精密加工、精确定位、振动主动控制等领域具有重要的应用前景［1－3］.

GMM的工作原理是在磁场作用下产生伸长或缩短，因此GMA的驱动磁场设计对其性能的发挥至关重要.超磁致伸缩执行器的磁场包括激励磁场和偏置磁场两部分.由于超磁致伸缩材料本身磁导率较低，使GMA的磁路尤其是永磁偏置磁路在应用过程中出现漏磁较大，GMM棒中磁场强度分布不均匀等问题，从而限制了GMM执行器的广泛应用，因此基于超磁致伸缩材料执行器的磁路优化成为当前国内外相关领域学者的研究热点.如S.Karunanidhia等采用了圆筒式永磁体提供偏场［4］;A.Lovisolo等设计了三分段的永磁偏置磁路［5］;唐志峰［6］、杨斌堂［7］等分别对激励磁路进行了优化设计，均取得了有益的结果.

本文在分段补偿均匀磁路的研究基础［8］上，根据磁场均匀性高和场外漏磁小的设计目标，分别对GMA的偏置磁场和激励磁场磁路进行了优化设计，提出一种新型内置永磁偏置的双磁体组合补偿磁路.

1 超磁致伸缩执行器磁路设计

图1为TbDyFe超磁致伸缩材料的典型磁致伸缩曲线.根据曲线的线性情况，可以分为Ⅰ，Ⅱ，Ⅲ3个阶段.其中，第Ⅰ阶段为磁致应变起始段，第Ⅲ阶段为磁致应变饱和段，皆存在较强的非线性，只有在第Ⅱ阶段时磁致应变与外加磁场呈现较好的线性关系.因此，用于微位移与微振动主动控制应用的GMA，一般都设计一个偏置磁场，使GMM棒产生一预应变，将执行器的初始工作点移到线性度较好区域的中心点，使执行器的位移输出与输入电流成近似线性关系，同时又消除了GMM在正负磁场下均随磁场增大而伸长所导致的倍频现象［9］，使执行器产生伸缩对称且线性度较好的磁致应变输出，以利于对执行器输出位移的精确控制.

激励磁场主要提供GMM棒发挥应用中所需大小磁致伸缩性能的外磁场，是执行器的控制驱动磁场.激励磁场的线性段是在一个范围内，由于偏置磁场的存在，激励磁场是关于零点对称的交变磁场.激励磁场通常由通电螺线管提供，在螺线管中通入可控的交变电流即可产生相应的交变磁场，从而获得所需的应变输出.

磁致伸缩材料内部磁通量分布均匀与否将影响执行器的磁致伸缩效果.由前期研究结果可知，GMM棒中磁场分布越均匀，GMA输出的磁致应变曲线越规则，否则会出现较多的毛刺谐波［10］.因此，超磁致伸缩执行器磁路设计目标之一就是使超磁致伸缩材料在驱动时其内部具有尽可能均匀的磁场分布.

由于超磁致伸缩材料的磁导率偏低(μr=3～5)，而材料棒一般尺寸较大，远大于普通磁路的狭小工作气隙，因此漏磁不可避免.较大的漏磁一方面会损失磁能，降低磁能利用率，另一方面在2个以上执行器紧密布置的系统中，执行器的漏磁场会相互影响，不但会使执行器的最终性能偏离设计值，甚至可能会影响整个系统的工作稳定性.因此减小场外漏磁是超磁致伸缩执行器磁路设计的另一个重要目标.

综上所述，GMM执行器磁路设计的原则，即是使超磁致伸缩材料在应变方向的磁场分布尽可能均匀，且执行器的场外漏磁尽可能小.

1.1 偏置磁路设计

常用的偏置磁场可由永久磁铁和螺线管提供，对于螺线管提供偏置磁场的磁路而言，偏置磁场大小可通过调节线圈中的电流而很方便地改变，但由于偏置线圈需要长期通入较大电流，电流产生的热效应会对超磁致伸缩材料的磁致伸缩性能产生较大影响，而采用永磁体提供偏置磁场则可以避免这个问题.故本文针对永久磁铁偏置的磁路结构进行了优化设计.

在GMA中，磁导率较低的超磁致伸缩棒可看作磁路的工作气隙.形成闭合磁路是减小漏磁的有效方法，因此采用内置式永磁偏置，以便外置磁导率高的软磁材料以闭合磁回路.首先，在磁致伸缩棒的两端放置2片柱状永磁体提供沿磁致伸缩棒长方向的磁场;其次，为降低磁路工作气隙的磁阻，在棒与永磁体之间加入导磁材料，使更多的磁通导入棒中;进而在2块永磁体的上下端均设有磁轭，与激励线圈外的软磁套筒一起，形成完整的闭合磁路进行磁屏蔽，从而有效减小漏磁.

利用ANSYS有限元对磁路进行分析发现，由于GMM棒的磁导率较低，当在棒两端加入永磁体后，棒中的偏置磁场强度分布呈现“两边高、中间低”的态势.因此，为了改善磁场分布的均匀性，在磁场较弱的棒的中间区域，增设了一个永磁套筒进行补偿，其与纵向的柱状永磁体极性相反，一方面可提高中间部分的磁场强度，同时抵消棒两端部分较高的磁场强度，从而使整个棒的偏置磁场的强度分布趋于均匀.总体磁路结构如图2所示.

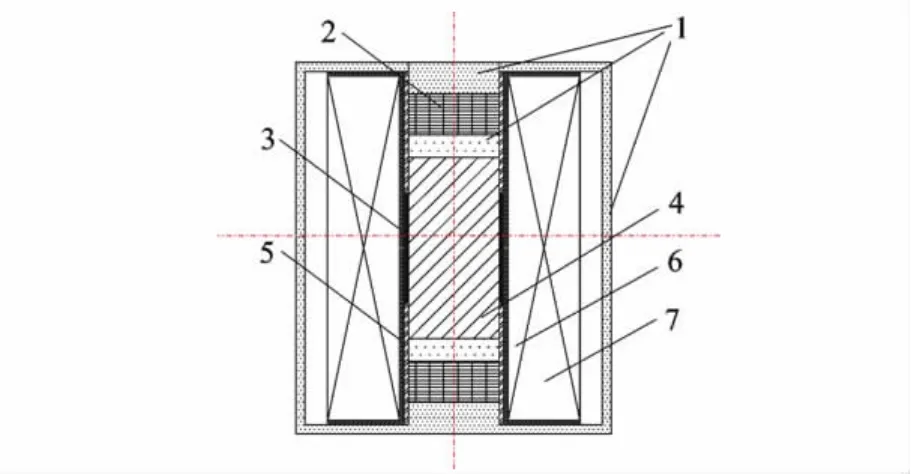
图2 磁路结构简图

1.2 激励磁路设计

不同长径比β(β=lc/dc，lc和dc分别为螺线管的轴向长度和外径)的螺线管内部的磁场分布不同［11］，图3为不同长径比下螺线管内部的磁场分布.可以看出:①长径比β很小时，螺线管内部的磁场很不均匀，中间偏高，两端偏低;当长径比β逐渐增大时，磁场分布逐步变得均匀，中间均匀区域变大，之后磁场分布随着长径比的增大变化不明显.②从单个螺线管的内部磁场的分布曲线上可以看出，处于螺线管两端的部分漏磁较大，磁场强度降低明显，所以螺线管内部的磁场分布呈现明显的“中间高、两边低”的现象.

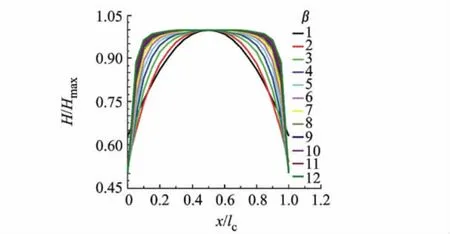
图3 不同长径比的螺线管内部的磁场分布

设计时，首先根据磁场强度及尺寸要求，选取合适长径比的螺线管尺寸，使螺线管中间的磁场分布较为均匀.为改善螺线管两端磁场偏低的现象，获得沿棒长方向磁场的均匀分布，在棒的两端加入软磁材料的同时，在永磁体的外围加磁轭及软磁套筒，使偏置磁路和激励磁路同时形成一个整体的闭合磁路，提升激励磁场两端磁场强度并减小漏磁.

2 ANSYS有限元仿真计算

2.1 偏置磁路仿真计算

由于GMA的轴对称性，取磁路结构的一半进行建模［12］，经过ANSYS有限元分析计算可得磁路中的磁力线分布，如图4所示.

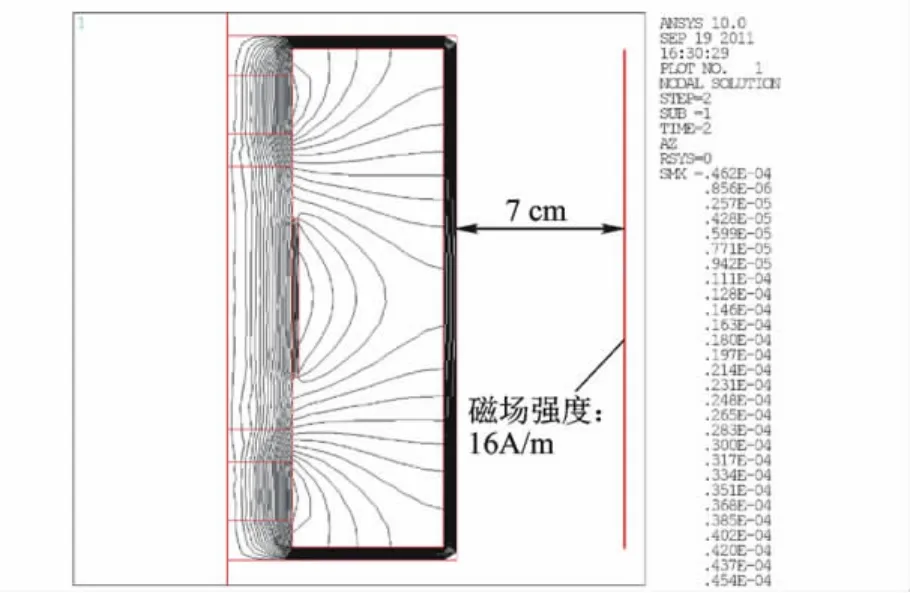
图4 偏置磁路的磁力线分布图

从图4中可看出TbDyFe棒中磁力线较密，磁能利用率较高.另外由于软磁的磁轭和套筒的磁屏蔽作用，执行器外无明显的磁力线分布.在指定位置(距离执行器7 cm)处，由ANSYS分析计算的漏磁场强度为16 A/m.

图5a所示为经过ANSYS计算后棒中的偏置磁场强度分布云图，可以看出表示棒中心的磁场强度的颜色相同且棒的总体磁场强度也较均匀;图5b所示为棒中心的偏置磁场强度分布曲线.

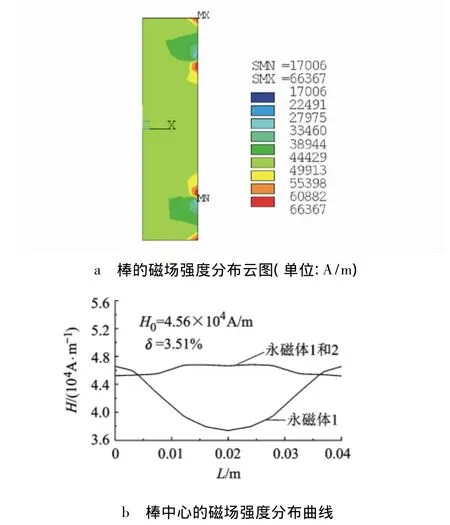
图5 超磁致伸缩棒的偏置磁场分布

为了表征磁场均匀性，定义磁场不均匀度为δ=|(H－H0)/H0|的最大值(H0为磁场分布的平均值)，实际应用中δ一般应小于10%.图5b可见，当磁路中只有永磁体1时，棒总体的磁场强度较低而且磁场均匀性较差，此时δ=21.3%，当加入极性相反的永磁体2时，棒两端的磁场强度略有降低，中间部分的磁场强度得到了提高，总的磁场均匀性有了明显的改善，此时δ=3.51%.

2.2 激励磁路仿真计算

图6为经计算后磁路中激励磁场的磁力线分布，可看出由于软磁的磁轭和套筒的磁屏蔽作用，执行器外磁力线很少，由ANSYS计算结果可得在场外指定位置(距离执行器7 cm)处的漏磁场强度为14.4 A/m.且TbDyFe棒中磁通密度强，表明具有较高的磁能利用率.如图7所示为超磁致伸缩棒的激励磁场强度分布曲线，棒中心部分的激励磁场约为44 000 A/m，在超磁致伸缩材料的应变方向上的磁场强度与偏置场相当;磁场分布不均匀度δ=8.73%，较好地满足了设计要求.

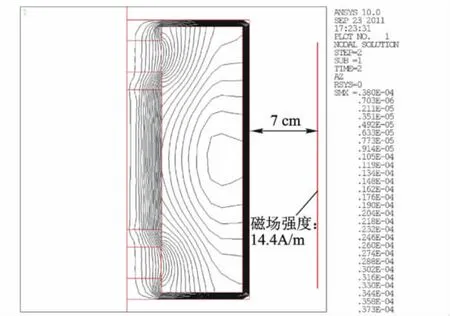
图6 激励磁路的磁力线分布图

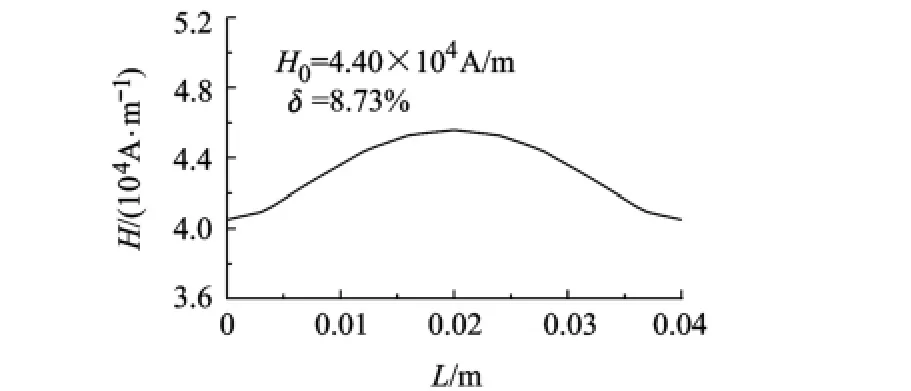
图7 超磁致伸缩棒的激励磁场分布

3 结论

本文提出了一种适用于超磁致伸缩材料执行器的新型内置式永磁偏置闭合磁路，并采用双磁体补偿组合结构，实现了磁场分布均匀、漏磁小的设计目标.经过优化设计后，通过ANSYS模拟计算，沿磁致伸缩棒长方向偏置磁场不均匀度δ＜5%，激励磁场不均匀度δ＜10%，执行器场外指定位置的漏磁＜80 A/m，符合了实际应用要求，为超磁致伸缩材料执行器在各种高科技领域的应用奠定了重要基础.

References)

［1］Grunwald A，Olabi A G.Design of a magnetostrictive(MS)actuator［J］.Sensor and Actuators，2008，144:161－175

［2］马志新，周志平.基于超磁致伸缩材料微位移驱动器的原理及实验研究［J］.现代机械，2009(2):19－21

Ma Zhixin，Zhou Zhiping.Design and experimental analysis of a micro-displacement actuator based on giant magnetostrictive material［J］.Modern Machinery，2009(2):19－21(in Chinese)

［3］张旭辉，刘永光，付永领.磁致伸缩作动器结构优化设计［J］.压电与声光，2009，31(3):377－380

Zhang Xuhui，Liu Yongguang，Fu Yongling.Optimum design of the magnetostrictive actuator［J］.Piezoelectectrics ＆ Acoustooptics，2009，31(3):377－380(in Chinese)

［4］Karunanidhia S，Singaperumal M.Design，analysis and simulation of magnetostrictive actuator and its application to high dynamic servo valve［J］.Sensor and Actuators A:Physical，2010，157(2):185－197

［5］Lovisolo A，Roccato P E，Zucca M.Analysis of a magnetostrictive actuator equipped forthe electromagnetic and mechanical dynamic characterization［J］.Journal of Magnetism and Magnetic Materials，2008，320(20):915－919

［6］唐志峰，项占琴，吕福在.磁致伸缩执行器的优化设计和控制模型［J］.中国机械工程，2005，16(9):753－756

Tang Zhifeng，Xiang Zhanqin，Lü Fuzai.Optimal design of magnetostrictive actuator and its control model［J］.Chinese Mechanical Engineering，2005，16(9):753－756(in Chinese)

［7］杨斌堂，陶华，Bonis M，等.Tefeno1-D磁致伸缩微小驱动器磁路设计［J］.机械科学与技术，2005，24(3):293－296

Yang Bintang，Tao Hua，Bonis M，et al.Magnetic circuit design for Tefeno1-D driven magnetostrictive mini-actuator［J］.Mechanical Science and Technology，2005，24(3):293－295(in Chinese)

［8］Zhang Tianli，Jiang Chengbao，Xu Huibin，et al.Permanentmagnet longitudinal fields for magnetostrictive devices［J］.Journal of Applied Physics，2007，101(3):034511

［9］朱金才，顾仲权.磁致伸缩作动器的设计及其动态特性研究［J］.南京航空航天大学学报，2006，30(4):413－418

Zhu Jincai，Gu Zhongquan.Design of magnetostrictive actuator and research of its dynamic characteristics［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2006，30(4):413－418(in Chinese)

［10］徐峰，张虎，蒋成保，等.超磁致伸缩材料作动器的研制及特性分析［J］.航空学报，2007，33(12):1436－1439

Xu Feng，Zhang Hu，Jiang Chengbao，et al.Designing and performance research of giant magnetostrictive actuator［J］.Acta Aeronautica et Astronautica Sinica，2007，33(12):1436－1439(in Chinese)

［11］Raghavendra A.High frequency high amplitude magnetic field driving system for magnetostrictive actuators［D］.Baltimore County Baltimore，MD:Mechanical Engineering，University of Maryland，2009

［12］孙明礼，胡仁喜，崔海蓉，等.ANSYS10.0电磁学有限元分析实例指导教程［M］.北京:中国机械出版社，2007:17－63

Sun Mingli，Hu Renxi，Cui Hairong，et al.Examples tutorials of ANSYS10.0 electromagnetic finite element analysis［M］.Beijing:China Machine Press，2007:17－63(in Chinese)