不同介质地下爆炸的地震耦合效应＊

肖卫国，王肖钧，朱号锋，靳 平

（1.中国科学技术大学近代力学系，安徽 合肥 230026；2.西北核技术研究所，陕西 西安 710024）

地下强爆炸瞬间释放出的巨大能量可以使周围岩石发生熔化和气化，形成迅速向外扩张的爆炸空腔，同时在岩石中产生强度远高于材料强度的冲击波。由于几何扩散效应和介质变形破坏所引起的能量耗损，冲击波在传播过程中会迅速衰减，当冲击波的强度低于材料的屈服强度后，便以地震波的形式向外传播。以地震波形式向外传播的爆炸能量与爆炸总能量之比称之为爆炸的地震耦合效率，其数量级一般在10－3～10－2之间。虽然地下爆炸转化为地震能量的比率很低，但地震波可以传播很远并被远区地震台站所记录，因此如何从地震台站记录中获取更多的源区信息，对于地下爆炸的远距离监测具有重要的意义。

地下爆炸的地震耦合效应除了直接和爆炸当量有关外，还和爆炸源区的介质特性、爆炸方式和埋深有关。早期研究大多利用有限几次地下核爆炸测试数据，定性分析介质特性对地下爆炸地震耦合效应的影响［1－3］，结果表明岩石的剪切强度和干孔隙率是影响地震耦合效应的最重要因素。20世纪90年代以后，由于暂停核试验条约的签署和核试验数据的逐步解密，特别是前苏联核试验数据的解密，极大地激发了学者们的研究热情和兴趣，推动了地下爆炸地震耦合效应研究的进一步发展。其中最具代表性的工作有：M.D.Denny等［4］系统回顾了地下爆炸的震源函数模型理论，给出了源区介质特性和爆炸空腔半径、地震矩和源拐角频率之间的经验关系；J.R.Murphy［5］在研究分析内华达、塞米帕拉金斯克等试验场地核爆炸当量震级关系的基础上，总结了不同介质、埋深和爆炸方式对震级当量关系的影响。

和国外进行过的数千次核试验以及近半个世纪的研究相比，国内在地下爆炸地震耦合效应方面的研究相对较少。相关的研究工作主要有：钟放庆等［6］利用地运动数据，反演得到了硬岩介质中的地下爆炸震源函数，并比较了核爆炸和化学爆炸在震源函数方面的差异；周钟等［7］对水饱和花岗岩中地下爆炸进行的数值模拟，着重研究了含水量对地震耦合强度的影响；劳俊等［8］采用Euler和Lagrange相结合的有限差分算法对多孔隙岩石介质的震源函数开展了数值模拟计算，分析了空腔大小及孔隙率对震源函数的影响。

本文中从实验角度出发，拟对黄土、砂砾石和花岗岩等介质中进行的地下爆炸地震耦合效应开展研究，利用实测的地震数据获得地下爆炸的震源函数，着重分析材料强度和孔隙率在地下爆炸地震耦合效应中的作用，比较不同介质中的地下爆炸在地震耦合强度方面存在的差异。

1 地下爆炸震源函数理论

地下爆炸的震源函数可通过作用在弹性半径为rel上的1个压力脉冲在介质中所引起的弹性扰动来加以描述［9］。引入折合位移势ψ（τ）（reduced displacement potential，RDP）后，均匀各向同性无限介质中球对称源引起的位移场（r＞rel）可表示为

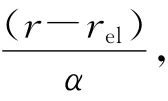
由此可求得用位移场u（r，t）表示的源函数

当τ→∞时，有ψ∞＝r2u∞（r），ψ∞为折合位移势的稳态值。

定义折合速度势γ（τ）＝，容易得到折合速度势和速度场的频率域关系［10］

容易证明，当ω→0时，折合速度势γ（ω）也将趋于ψ∞。这表明由频率域的折合速度势和时间域的折合位移势得到的稳态值是等价的，因此也可用γ（ω）表示地下爆炸的源函数。源函数模型大都具有4个典型的特征参数，即地震矩、源拐角频率、过冲和高频衰减因子。其中地震矩M0表示地震耦合强度，它与ψ∞的关系为

式（3）～（4）表明，记录自由场位移或速度数据（对于地表测量数据，则必须去除由于地表界面的反射和波型转换产生的影响），可求得地下爆炸时间域或频率域的震源函数，并由此得到地震耦合强度。

2 实 验

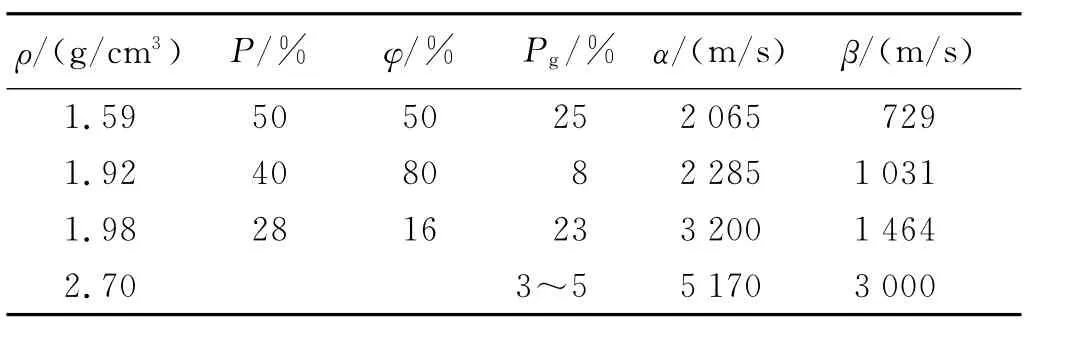
表1 介质的物性参数Table 1Material parameters

为比较不同介质中地下爆炸的地震耦合强度，分别在黄土、砂砾石和花岗岩等介质中进行了当量同为100kg级的1组地下爆炸实验。其中，花岗岩是低孔隙率高强度介质，黄土和砂砾石则是高孔隙率低强度介质。为考察水饱和度对地震耦合强度的影响，另选择了2个孔隙率接近但水饱和度相差较大的黄土实验场地，分别称之为黄土1和黄土2。

为确保爆炸后不形成喷发式弹坑或烟囱的出现，爆炸实验在封闭填实式的竖井中进行，实验埋深在15～20m之间。在爆心距350～5 000m范围内安放了10个以上测点进行速度测量，测点布局以降低测量本身带来的不确定度为宗旨。实验场地地质条件良好，介质均匀，测点台基介质与源区介质相同，测点与源区之间的介质可视为与源区相同。

实验中采用的地震计有2种，分别是Le－3Dlite型和Guralp－3ESPC型，它们均为0.5～80Hz频带之间速度平坦型的地震计。数据采集仪则使用北京港震机电设备有限公司生产的24位数采EDAS－24IP，采样率为500s－1。

实验前委托地质勘测部门对爆炸源区介质的密度、水饱和度和孔隙率进行了测量，如表1所示。表1给出了勘测部门提供的测量结果，其中：ρ为介质天然密度，P为孔隙率，φ为水饱和度，Pg为干孔隙率，α为纵波速度，β为横波速度。除花岗岩外，其余都是高孔隙率介质。表1中波速是直接利用爆炸产生的地震信号，其值由不同测点上测得的纵、横波经过的时刻和爆心距通过最小二乘法拟合得到的。图1是4种介质现场测得的纵波时程曲线。图中可以看出，纵波经过的时刻和爆心距基本上呈线性关系，说明了地震波传播路径上没有明显的波速异常体，即整个实验场地介质总体上是均匀的。

为直观了解不同介质中地下爆炸地震波的差异，图2分别给出了爆心距d＝4.8，4.9，5.0km测点上质点速度v的时程曲线，其中图2（a）、（b）、（c）分别表示花岗岩、黄土2和砂砾石中的测量结果。可以清楚地看到，对于不同介质中的地下爆炸，测点记录的波形有很大的差异：在距离相近的爆心距上，纵波峰值以水饱和黄土2最大，砂砾石次之，花岗岩最小；但从纵波的频率成分上看，花岗岩的波形周期最短、优势频率高，黄土的波形周期长、优势频率低，而砂砾石介于二者之间。

图1 不同介质中的纵波速度Fig.1Velocity of primary wave in different mediums

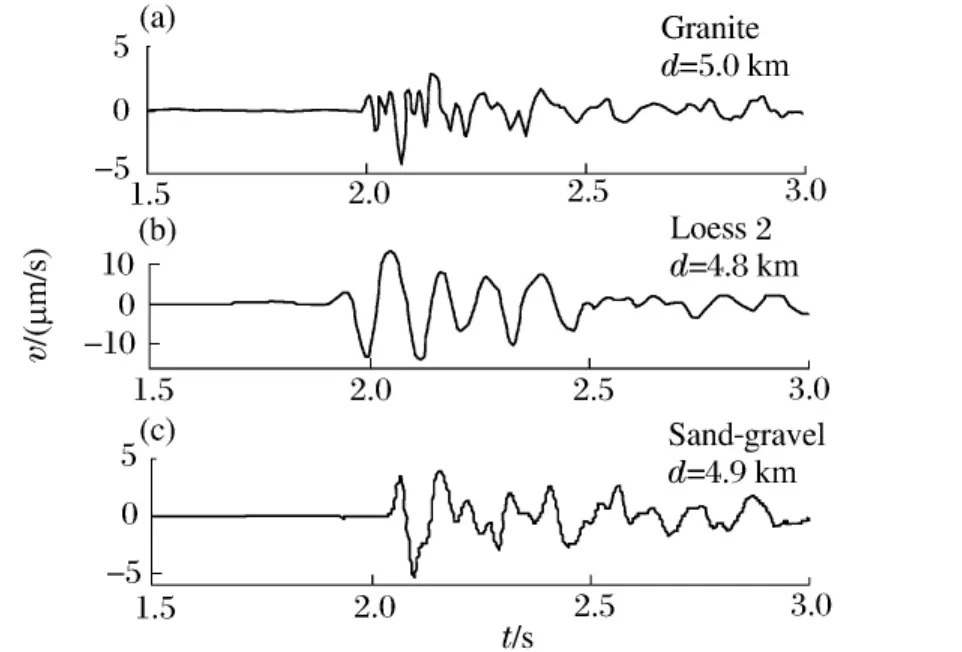
图2 爆心距相近处测点的记录波形Fig.2Explosion waveforms at similar distance

由于不同介质中地下爆炸激发的地震波信号优势频率存在较大差异，因此直接利用位移峰值的衰减规律来刻画地震耦合强度并不科学，也不准确。更为合理的方法是，直接通过实测波形计算地下爆炸的源函数及其地震耦合强度，然后分析不同的介质特性与地震耦合强度之间的关系。

3 不同介质地震耦合强度的差异

采用频率域求解震源函数的方法，首先由不同测点上的速度波形经傅立叶变换得到速度谱，然后由式（4）求得折合速度势的频谱，根据其高频衰减和过冲特征选择不同的源函数模型与之比对，进而确定能准确描述源频谱特征的震源函数模型。

图3给出了4种介质中部分测点上求得的源频谱γ（ω），其中子图对应着不同爆心距测点上得到的结果，图中同时还给出了与实测结果拟合较好的理论曲线。由图3可知，在大多数测点上理论模型和实测结果吻合良好。对于黄土和砂砾石，其爆炸源频谱和基于凝灰岩、冲积土得到的四阶Haskell源模型［11］比较吻合；而对于花岗岩，其爆炸源频谱则与基于硬岩得到的三阶H－H源模型［12］更接近，这表示软硬2种不同介质的地下爆炸源频谱有明显区别。

从图3还可以看出，同一介质不同测点的折合速度势也不尽相同，这反映了场地介质局部不均匀性以及地形起伏对测量结果的影响。将所有测点实测数据反演得到的地震耦合强度（对应于图中的低频稳态值）进行算术平均，结果列于表2。

M.D.Denny等利用大量地下核爆炸以及少量低当量化爆实验数据归纳得到

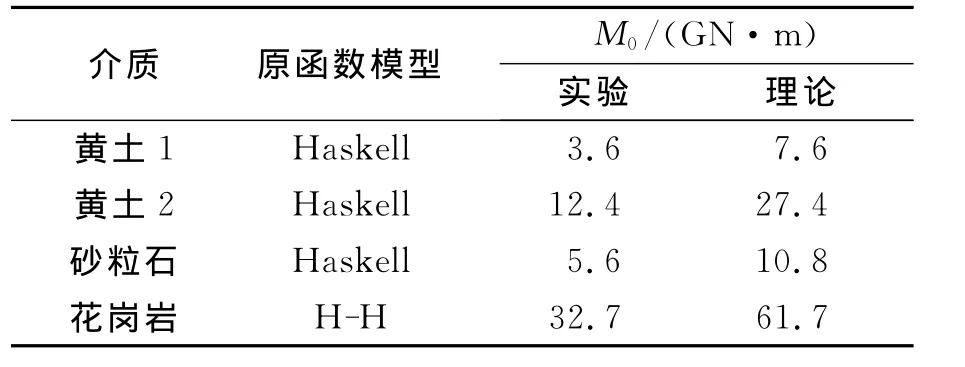
表2 不同介质中填实爆炸的源频谱参数Table 2Explosion source parameters for different material

式中：ρ为密度，g是重力加速度，h为埋深，α为纵波波速，β为横波波速，Pg为以百分数计的干孔隙率，W为爆炸当量。

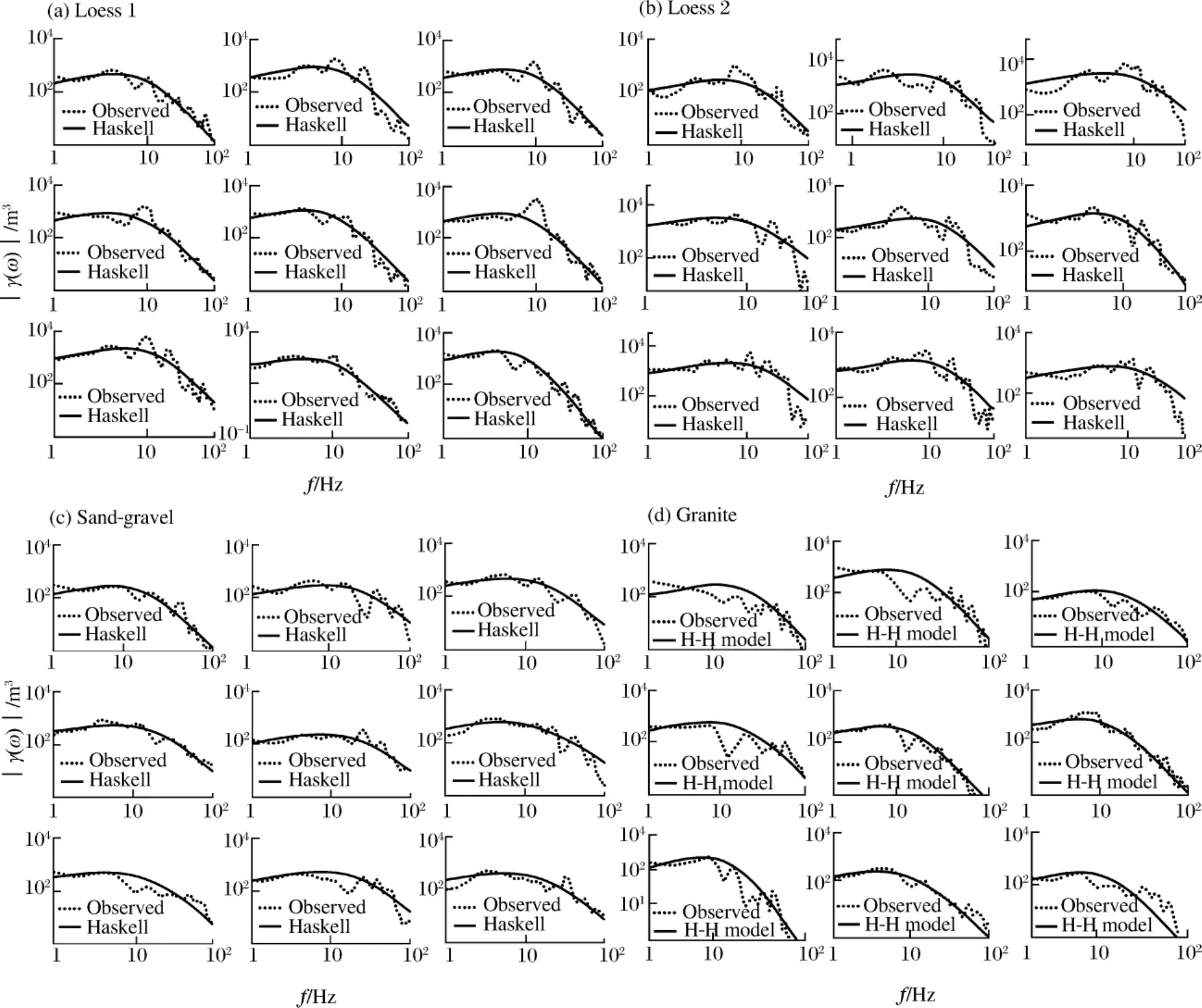
图3 实测RVP谱和理论模型比较Fig.3Comparison between observed RVP’s spectrum and theory model

依据式（6）以及表1中的介质参数可以求出由M.D.Denny等的经验公式确定的地震矩，其结果也列于表2。由表可见，实测结果与经验公式估算结果在趋势上是一致的，但在数值上有一定差异。说明M.D.Denny等的经验公式在描述介质参数与地震矩强度之间的关系方面具有一定的适用性。至于实测结果与估算结果存在的差异。一方面由于经验公式主要是由大当量地下核试验测量结果归纳得到的，而小当量化爆实验的样本并不充足；另一方面，经验公式中的材料参数只给出了干孔隙率、介质密度和波速等，并没有直接给出材料强度和水饱和度对源强度的影响，从物理上说这并不合理。因此，如果仅根据实测地震矩利用式（6）估算爆炸的实际当量将会存在较大的误差，特别是对于小当量浅埋深条件下的地下爆炸而言。对于式（6）存在的局限性和不足，根据更多的实验结果对式（6）进行修正是必要的，不过目前相应的实验资料和实验数据还不够丰富，这一工作可留待今后进行。

从表2中可以看出，地下爆炸地震耦合强度与介质物理属性有很大关系。在相同当量和埋深下，属于硬岩的花岗岩，其爆炸地震矩比软介质黄土和砂砾石大许多（前者约是后者的3～9倍），这说明介质强度是影响地下爆炸地震耦合强度的重要因素；而对于2个不同场地的黄土，虽然它们总的孔隙率相近（见表1），但水饱和度相差很大，地震耦合强度有明显差别。和干孔隙率为25%的黄土1相比，干孔隙率只有8%的黄土2中的地震矩大约是前者的3倍多，这说明水饱和度在地震耦合效率中起着很大的作用，同时也说明影响地震耦合强度的主要因素是干孔隙率而非单纯的总孔隙率；对于干孔隙率相近的黄土1和砂砾石（分别为25%和23%），因介质波速和密度的不同而引起的地震耦合强度也有近50%的差异。上述分析表明，通过现场实验，研究材料物理性能与地下爆炸地震耦合效应的关系是可行的，也是有意义的。

4 结 论

根据不同介质中地下爆炸实验的实际地震观测资料，利用经典的理论模型和方法获得地下爆炸源函数以及以折合速度势低频稳态值描述的地震耦合强度，并对地下爆炸地震耦合强度与介质特性间的依赖关系作了分析和讨论。得到的主要结论有：

（1）对地下爆炸地震耦合效应起重要作用的介质材料参数主要有介质的强度、干孔隙率、水饱和度、介质的密度和波速。在相同当量和埋深下，属于硬岩的高强度花岗岩的地震矩最大，比黄土、砂砾石等高孔隙低强度的介质大得多，前者的地震矩可以是后者的3～9倍；对于多孔介质，影响地震矩的主要因素是介质的干孔隙率而非单纯的总孔隙率，水饱和度在地震耦合效应中起着十分突出的作用。虽然黄土1和黄土2的总孔隙率相当，但是两者的含水量不同，干孔隙率相差很大，其地震耦合强度相差可达3倍多，这说明水饱和度和干孔隙率是影响地震耦合强度的重要指标。

（2）实验结果表明，黄土和砂砾石等软介质中的爆炸源频谱与四阶Haskell源模型比较吻合，而对于花岗岩这样的硬介质，其爆炸源频谱则与三阶H－H源模型更为接近。通过野外地下化爆实验，进一步考察了M.D.Denny等提出的经验公式在描述介质参数与地震矩关系方面的适用性，和在估算小当量地下爆炸地震耦合强度方面存在的局限性。

（3）采用小型地下化爆地震观测资料，可以有针对性地研究源区介质特性与地震耦合效应间的关系。但是试图通过目前有限的几次地下爆炸实验建立地震耦合强度的定量关系存在很大困难的，也是不现实的，有待今后一步开展实验工作。

［1］Werth C G，F.H.Roland.Comparison of amplitudes of seismic waves from nuclear explosions in four mediums［J］.Journal of Geophysical Research，1963，68（5）：1463－1475.

［2］Perret W R.Free－field particle motion from a nuclear explosion in salt［R］.VUF3012.Albuquerque，New Mexico：Sandia Corporation，1967.

［3］Larson D B.Explosive－induced wave propagation in nugget sandstone［J］.Journal of geophysical research，1984，89（B11）：9415－9424.

［4］Denny M D，Johnson L R.The explosion seismic source function：Models and scaling laws reviewed［R］.UCRLJC－107941.California：Lawrence Livermore National Lab，1989.

［5］Murphy J R.Types of seismic events and their source descriptions［C］∥Husebye E S，Dainty A M.Monitoring a Comprehensive Nuclear Test Ban Treaty：NATO ASI Series E.Dordrecht，Netherlands：Kluwer Academic Publishers，1996：225－245.

［6］钟放庆，李山林，孙恒仲，等.应用地运动数据反演地下爆炸震源函数［J］.爆炸与冲击，2005，25（2）：176－179.

ZHONG Fang－qing，LI Shan－lin，SUN Heng－zhong，et al.Seismic source function for an underground explosion［J］.Explosion and Shock Waves，2005，25（2）：176－179.

［7］周钟，王肖钧，肖卫国.花岗岩介质中地下爆炸震源函数研究［J］.爆炸与冲击，2007，27（1）：18－25.

ZHOU Zhong，WANG Xiao－jun，XIAO Wei－guo.Study on the main characteristics of underground explosion seismic source function in granite［J］.Explosion and Shock Waves，2007，27（1）：18－25.

［8］劳俊，肖卫国，王肖钧.地下空腔解耦爆炸的数值模拟研究［J］.爆炸与冲击.2009，29（5）：535－541.

LAO Jun，WANG Xiao－jun，XIAO Wei－guo.Numerical study on the underground cavity－decoupling explosion［J］.Explosion and Shock Waves，2009，29（5）：535－541.

［9］Sharpe J A.The production of elastic waves by explosion pressures.Ⅰ：Theory and empirical field observations［J］.Geophysics，1942，7（2）：144－154.

［10］Mueller R A，Murphy J R.Seismic characteristics of underground nuclear detonations PartⅠ：Seismic spectrum scaling［J］.Bulletin of the Seismological Society of America，1971，61（6）：1675－1692.

［11］Haskell N A.A static theory of the seismic coupling of a contained underground explosion［J］.Journal of Geophysical Research，1961，66（9）：2937－2944.

［12］Helmberger.D.V.，and D.M.Hadley，Seismic source functions and attenuation from local and teleseismic observations of the NTS events jorum and handley［J］.Bulletin of the Seismological Society of America，1981，71（1）：51－67.