病毒最大有效接触率的近似计算
2012-06-19李军红李香玲
李军红 崔 宁 李香玲
(河北建筑工程学院数理系,河北 张家口075024)
1 引 言
传染病是由病原微生物(病毒、立克次体、细菌、螺旋体等)和寄生虫(原虫和蠕虫)感染人体后产生的有传染性的疾病[1].一直以来传染病就是人类健康的一个长期而严峻的威胁,特别是近年来一些新型传染病毒(如SARS和H1N1)的爆发,并表现出明显的全球扩散的趋势,针对这种大尺度传染病所建立的数学模型的预测结果往往与事实不符[2].然而,一种病毒能够给人类带来生存威胁和重大损失,它应具有一定的接触率、致死率、传播途径和传播能力,这就需要全面考虑病毒携带者(种子病人)的数量及其在健康人群中的分布,被传染者的数量,传播形式及病毒本身的传播能力,而病毒的有效接触率是影响传播途径和传播能力的主要因素,也是疫情控制的重点.
一般地,把接触率看作总人口数N的函数C(N)[3],它反映了染病者的活动能力、环境条件等因素,在染病者和易感者的的一次接触中,如染病者能将疾病传给易感者,那么称这样的一次接触为一个有效接触.接触率与传染概率β的乘积为单位时间内一个染病者的平均有效接触数,称其为有效接触率.在流行病模型中,常用的接触率一般有两种:双线性传染率和标准传染率[4].文中针对新发传染病的流行病学特点[5],结合Logistic模型研究疫情初期的有效接触率,称之为最大有效接触率.基于双线性传染率模式给出一种近似计算方法来反映有效接触率,从而,为更好地了解突发疫情和制定控制措施力度提供理论依据.
2 最大有效接触率计算
假设mS、mE、mI分别为初始时刻易感者、潜伏者和传染者人数,r0和d0分别为此时刻病毒携带者的相对增长率和死亡率.在疫情初期,病毒携带者的增加大致符合具密度制约的Logistic增长模型,通过考察Logistic增长曲线[6]可知,在接近病毒传播的初始时刻的时间段内密度制约对病毒携带者的增长影响很小,可近似认为病毒携带者的增加符合Malthusian方程,另外,易感者由于受传染病的影响,其人数随时间变化的变化率与当时易感者的人数和当时染病者的人数之积成正比[7],同时假定所研究的较短的时间内没有人口的自然出生与死亡,那么在不考虑人的自我保护意识等其它干扰因素下,应该有单位时间上易感人数的减少量等于单位时间上病毒携带者的增加与死亡人数之差,即
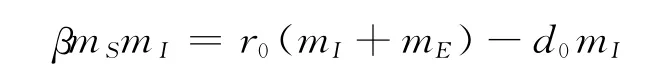
整理得

由(2.1)可知,潜伏者的增加将会使传染者增加和易感者减少.
然而在实际中,初始时刻的相关数据我们很难掌握,出现疫情就会有人的自我防护意识和各项应急措施的介入等等,这会使病毒携带者的相对增长率的值受较大影响,除非在实验室中才能得到较精确值,为避免这一误差,我们将(2.1)变形为:
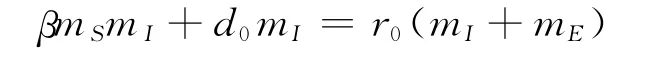
如果测得接近初始时刻的相邻两组值mS0,mE0,mI0,d0,mS1,mE1,mI1,d1,由
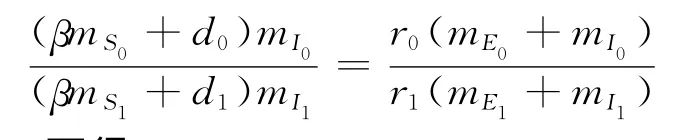
以及在足够小的时间段内r0≈r1,可得
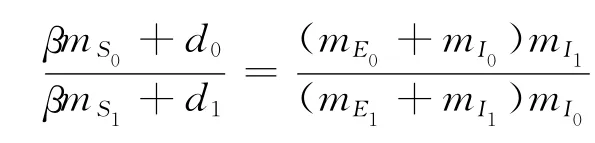
因此,可求得传染概率的实际计算公式
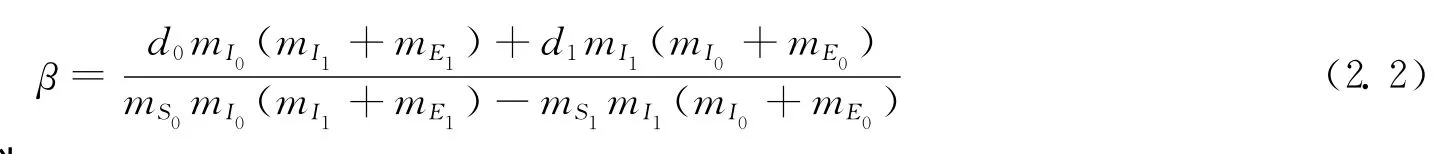
所以可得最大有效接触率为
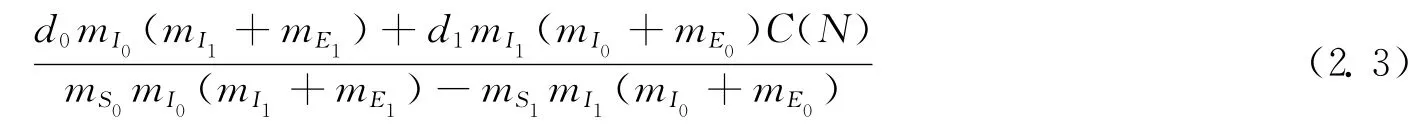
从而可以近似计算病毒在标准传染率和双线性传染率机制下最大有效接触律的近似值.
在实际中,单位时间上的潜伏者人数、感染者人数和易感者人数,可分别由单位时间上的疑似病人数、显症病人数、健康人数来代替;死亡率用死亡人数与感染人数的比例来近似表示.由于测量、判断失误等原因,我们只能近似的认为刚发现疫情的时刻为初始时刻,因此计算所得的数值比实际的要小,但这并不影响控制措施的制定.
潜伏者的隔离不仅是困难的,而且对疫情的控制具有举足轻重的作用,反映到实际中是对疑似病例的隔离.实际中由于潜伏者具有隐蔽性,所以,如果我们测得某一时段的传染者人数和死亡率,结合上一时段的潜伏者、传染者人数和死亡率利用公式就能得出此时段的潜伏者人数,如果所得潜伏者人数与实际相差较大,就说明病毒在此期间已经发生了变异,控制措施就要相应的发生改动,还可以考察每时刻的βtmS值是否发生改变,以此来衡量病毒是否发生了变异,其中βt为此时病毒的传染概率.
3 实例验证
本文以SARS为例,结合文[8]的数据,来说明最大有效接触率近似求法的可行性.北京市的人口数量为13820000,将4月20日作为初始时刻,结合4月21日数据,可得:

由(2.3)可得SARS病毒传染概率大致为:β=2.0385×10-7,如果以每天为单位,疫情在双线性传播模式下和无防范传染的情况下,病毒的最大有效接触率,13820000β=2.806628,因此,每个传染者每天大致可传染2.8个人,也就是说,一个传染者可造成约2.8的指数次增长,此结果与文[9]的3.15相差0.3,但由于参照数据有治愈率的影响,以及距离初始时刻有一段时间,因此,计算所得的数值比实际的要小.对北京市来说,从4月20日到6月23日动态系统中每天的三类人群数的具体数据是很难精确掌握的,不过我们通过近似计算βtmS的值都大致等于2.8,与初始时刻值几乎吻合,可以说,在此期间SARS病毒没有发生变异.4月20日到4月21日疑似病例增加了208例,若以天为单位,则北京市此时应有至少8例传染者和24例潜伏者需要隔离,由于测量值与实际值有浮动,不过针对突发疫情,需要在尽可能大的范围内加以控制,所给计算方法所的结果较能真实地反映实际疫情的传播,可用于预测疫情的传播和病毒的变异,为突发疫情控制措施的制定提供了理论依据.
[1]彭文伟.传染病学.北京:人民卫生出版社,2001
[2]Meyers L A,Pourbohloul B,Newman M E J,etc.Network theory and SARS:Predicting outbreak diversity.232(1):2005 J.Theor.Biol.71~81
[3]Horst R.Thieme and C.Castillo-Chavez,On the Role of Variable Infectivity in the Dynamics of the Human Immunodeficiency Virus Epidemic In:C.Castillo-Chavez(Eds.),Mathematical and statistical Approaches to AIDS Epidemiology.Lect.Notes Biomath.Vol.83.Berlin Heidelberg New york,Springer-Verlag,1989,157~177
[4]J.Mena-Lorca,H.W.Hethcote,Dynamic models of infectious diseases as regulators of population sizes.J.Math.Biol.,30(1992):693~716
[5]李铮,陈曦等.SARS流行病传染动力学研究.生物化学与生物物理进展.2004,31(2):167~171
[6]马知恩.种群生态学的数学建模与研究.合肥:安徽教育出版社,1996,13~14
[7]杨光,张庆灵.对传染病数学模型(Kermack-Mckendrick模型)施加控制的阈值分析.生物数学学报,2004,19(2):180~184
[8]http://www.beijing.gov.cn/Resource/Detail.asp?ResourceID=66070
[9]黄德生,关鹏,周宝森.SIR模型对北京市SARS疫情流行规律的拟合研究.疾病控制杂志,2004,5(8):398~401
