钢－预应力混凝土混合连续箱梁桥钢箱长度参数研究＊

丁 威 何雄君

（武汉理工大学交通学院 武汉 430063）

0 引 言

钢－预应力混凝土混合连续箱梁桥是借鉴钢－混凝土叠合梁桥技术发展起来的，使之成为更加适宜平原区通航河道推广应用的新型桥梁结构.它将承受正弯矩部分采用钢结构，而承受负弯矩部分采用预应力混凝土结构，充分发挥2种材料不同的物理力学性能特点，最大限度地追求高性能、低造价［1］，形成强度高、刚度大、动力性能好的结构形式，可以减少自重，降低造价，节约模板并减少支模工序从而缩短施工周期.不仅可以很好地满足结构的功能要求，而且还具有良好的技术经济效益，在桥梁结构领域显现出广阔的应用前景［2］.

关于钢箱长度的选择，确定钢箱与混凝土箱梁相结合的位置是设计的一个关键环节.钢和混凝土这两种材料相互结合，易引起界面滑移、竖向掀起［3］，故在结构设计中要求能比较流畅地传递各种荷载产生的内力及变形.另外结合部位置应具有良好的抗疲劳性和耐久性，在外形上也要求钢箱梁和混凝土箱梁的过渡比较柔和一致.本文以浙江318国道长桥大桥——三跨预应力混凝土混合连续箱梁桥为例，采用MIDAS／Civil软件建立了不同的钢箱长度参数的模型，计算分析了恒载与活载下的关键截面随钢箱长度参数变化的力学特征，研究了反弯点位置随钢箱长度参数变化的规律，得到一些合理选择钢箱长度参数，实现结构优化的一些结论.

1 结构构造

主桥上部结构采用45m＋80m＋45m 变截面钢混合连续箱梁（见图1），主跨为65m 预应力混凝土变截面箱梁＋40m 钢梁＋65m 预应力混凝土变截面箱梁.其中：跨中40 m 钢梁（横断面图见图2），梁高均为1.5m，纵向分5片工厂化制作，边箱宽度为2.75m，次边箱宽度为2.174m，中箱宽度为2.202m，现场吊装焊接；预应力混凝土变截面箱梁高度按二次抛物线变化，主墩支点处梁高4.5m，边墩支点处梁高1.7m，中跨与钢箱梁相接处梁高1.5m，采用单箱双室断面，顶宽12.25m，底宽8.75m，悬臂长1.75m.设计荷载等级为：公路I级，抗震设防烈度为IV 度.

图1 318国道长桥大桥主桥立面图（尺寸单位：cm）

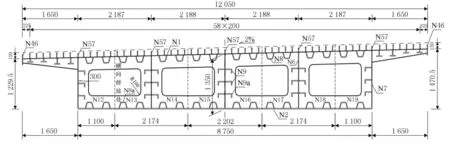
图2 318国道长桥大桥钢箱梁横断面图（单位：mm）

G318国道长桥大桥钢混结合段采用设置钢接头实现干接法连接，其具体结构见图3、图4.

图3 G318国道长桥大桥钢混连接构造图

图4 钢接头构造图

通过制作钢接头，并将钢接头预埋至混凝土箱梁中跨悬臂端，实现混凝土箱梁与钢箱梁之间焊接连接.

2 理论分析

假设上部结构为等截面梁，将其中跨分成3等份，每份长26.67 m.假定只考虑自重效应，跨中部分的自重集度为P1，其余部分的集度为P2［4］，见图5.

可以计算出跨中支点处负弯矩为186.8P1＋270.1P2，跨中截面正弯矩为257.7P1＋85.4P2，而钢箱梁的重量大约相当于等效混凝土梁重量的30%，支点负弯矩和跨中正弯矩将会减小大约1／3，对大跨径的混凝土桥梁来说，降低1／3的负弯矩（中间2支座处）是非常有利的.

基于上述理由，跨中钢梁越长，中间两支座处负弯矩绝对值越小，增大了中跨的跨越能力，但是钢箱梁的造价远高于混凝土梁，如果再考虑造价因素，从理论上可以估算出钢箱梁节段的合理长度.

图5 跨中钢箱的合理长度（单位：m）

3 数值分析

3.1 计算模型

结合现行的桥梁设计规范［5－6］，以杆系理论为基础，采用通用有限元软件MIDAS／Civil对其进行设计计算.本文只针对桥梁上部结构进行计算与分析研究，故只对上部结构建模，不考虑下部结构.每个模型由172个节点，93个单元组成.主梁采用C50混凝土，预应力采用1860 MPa钢绞线.模型计算时荷载包括梁的自重、预应力、二期恒载、活荷载等.结构计算模型见图6.

图6 结构计算模型

3.2 钢箱长度参数选择

由于钢混连接处是结构的薄弱部位，因此它应位于中跨弯矩反弯点附近（弯矩较小），即钢箱端部应离中跨弯矩反弯点不远.另一方面，根据上面的理论分析，钢箱梁长度的确定，应使中间两支座处负弯矩及中跨跨中正弯矩绝对值较小，满足所要求的中跨跨越能力.这是钢－预应力混凝土混合连续箱梁桥钢箱长度参数的确定原则.

通过对原始模型的钢箱长度参数做一些改变，考虑钢箱长度取为主跨（80 m）的0.4～0.6之间变化，按32，36，37，38，39，40，41，42，43，44，48m 这一系列不同的钢箱长度参数进行变化，其他参数均相同.由此分别建立了11个类似于如图5所示的计算模型来探讨3 跨钢－预应力混凝土混合连续箱梁桥中跨钢箱长度参数规律.

3.3 恒载、活载弯矩随钢箱长度参数变化规律

这里恒载包括自重、二期荷载、混凝土收缩徐变作用、次内力效应作用.活荷载主要针对的是车辆荷载作用，不考虑其偏心作用.恒载作用下结构的弯矩形状见图7.研究的重点放在钢箱上，仅列出钢箱梁跨中截面弯矩随钢箱长度参数变化如表1所列［7］.

图7 主桥结构的弯矩图

表1 钢箱梁跨中截面弯矩随钢箱长度参数变化

3.4 恒载与组合荷载作用下反弯点位置随钢箱长度参数变化规律

中跨结构存在2个对称弯矩零点（即反弯点，见图7）.恒载和组合荷载作用下反弯点之间的距离（反弯点间距）随钢箱长度参数变化见表2.反弯点间距也表示钢箱梁两反弯点之间的受正弯矩区域范围的长度.

进一步，恒载和组合荷载作用下反弯点与钢箱梁端部的距离（反弯点端距）随钢箱长度参数变化见表3.反弯点端距也表示钢混连接位置的合理性.

表2 钢箱长度参数变化下2种荷载的反弯点距离 m

表3 钢箱长度参数变化下2种荷载的反弯点端距 m

根据表1、表2和表3，综合分析可知：

1）从表1来看，钢箱梁跨中截面恒载弯矩随钢箱长度的增大而减小，钢箱跨中截面活载弯矩随钢箱长度的增大而增大，但前者幅度比后者大.即总的来讲，钢箱跨中截面弯矩随钢箱长度的增大而减小.这也反证了理论分析的正确性.

2）表2说明了恒载和组合荷载作用下反弯点间距随钢箱长度参数变化.表3则说明，在钢箱长度为32 m 时，反弯点与钢箱梁端部的距离最小，即钢混连接位置总弯矩最小，便于钢混连接分析与设计.但此时钢箱梁跨中截面正弯矩与2支点截面的负弯矩绝对值却最大，也就是说中跨跨越能力相对最小.318国道长桥大桥钢箱梁选用40m，是同时综合考虑反弯点位置与中跨跨越能力所确定的.

4 结束语

钢箱梁长度是钢－预应力混凝土混合连续箱梁桥设计的一个重要参数.通过对钢－预应力混凝土混合连续箱梁桥的钢箱长度参数的研究，分析其力学特征.在主跨80m 的0.4～0.6倍范围内变化，结合恒载、活载作用计算，分析了关键截面处力学特征与反弯点位置.

钢箱长度的确定规则为：（1）钢箱端部应离中跨弯矩反弯点不远，使钢混连接处弯矩较小；（2）应使中间两支座处负弯矩及中跨跨中正弯矩绝对值较小，满足所要求的中跨跨越能力.本文318国道长桥大桥钢箱梁选用40m，是同时综合考虑反弯点位置与中跨跨越能力所确定的应用实例.

［1］刘玉擎.组合结构桥梁［M］.北京：人民交通出版社，2005.

［2］聂建国，刘 明，叶列平.钢－混凝土组合结构［M］.北京：中国建筑工业出版社，2005.

［3］Ayoub A.A force－based model for composite steelconcrete beams with partial interaction［J］.Journal of Constructional Steel Research，2005，61（3）：387－414.

［4］唐建华，向中富，冯 强，等.特大跨连续刚构桥研究与实践：重庆长江大桥复线桥［M］.北京：人民交通出版社，2008.

［5］中华人民共和国交通部.JTG D60－2004公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.

［6］中华人民共和国交通部.JTG D62－2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［7］吴中鑫，杨 平.钢－预应力混凝土组合梁抗扭极限分析［J］.武汉理工大学学报：交通科学与工程版，2010，34（2）：362－365.