复合受力作用下的板格和加筋板的极限强度计算与研究

崔虎威 杨 平

（武汉理工大学交通学院 武汉 430063）

0 引 言

在船舶设计与强度评估中，如果不能明确结构的极限承载能力，依旧单纯采用基于线弹性理论的许用工作应力方法，由于不能从根本上决定结构的真实安全极限已经不再适合当前的设计理念和发展要求.将基于极限强度的理论引入船舶结构的设计与强度评估比传统方法更加合理.IACS《双壳油船共同规范》也已将基于“极限强度”概念的非线性屈曲理论引入到技术标准之中，并于2006年4月1日起开始施行.

在设计工作中，准确地计算和预测结构的极限强度对于确定结构的安全极限十分重要.虽然多年来对结构极限强度已有很多理论研究、数值计算、模型试验方面的研究工作和成果，但在实际工程运用上仍有相当差距.国际船舶与海洋工程领域内的学术组织ISSC（国际船舶结构大会）近年来组织了国际上多所研究机构和大学的知名学者对船体极限强度作了较为深入的研究，但研究的结果表明，尽管采用相同的结构参数、材料特性、初始缺陷和载荷工况，相互间的结果仍非常分散，而且与试验也不甚吻合［1］.因此ISSC近年来一直在开展关于结构极限状态的研究工作，其中包括对板格，加筋板以及船体梁分别采用非线性FEM 进行标定计算［2－4］.

影响板格和加筋板极限强度的因素有很多，其中主要有焊接导致的初始缺陷，即焊接变形及焊接残余应力，海水腐蚀等等.初始变形在很大程度上影响板格和加筋板极限强度的大小，因此在各种计算方法中，初始变形是首要考虑的影响因素.在使用非线性FEM进行实际计算分析时，如何有效合理地施加初始变形，选取合适的单元尺寸去获得计算时间与计算精度的统一，以及边界条件的确定都将对极限强度的计算结果产生影响.

本文采用非线性有限元分别对一块板格和加筋板进行具体极限强度计算，来探究上述问题，并为结构非线性有限元计算提供参考.

1 结构建模与非线性有限元分析

1.1 板格和加筋板模型

在实际船舶的甲板板架或船底板架中，板格由纵骨和强横梁支持，加筋板由纵桁和横框架支持，见图1.

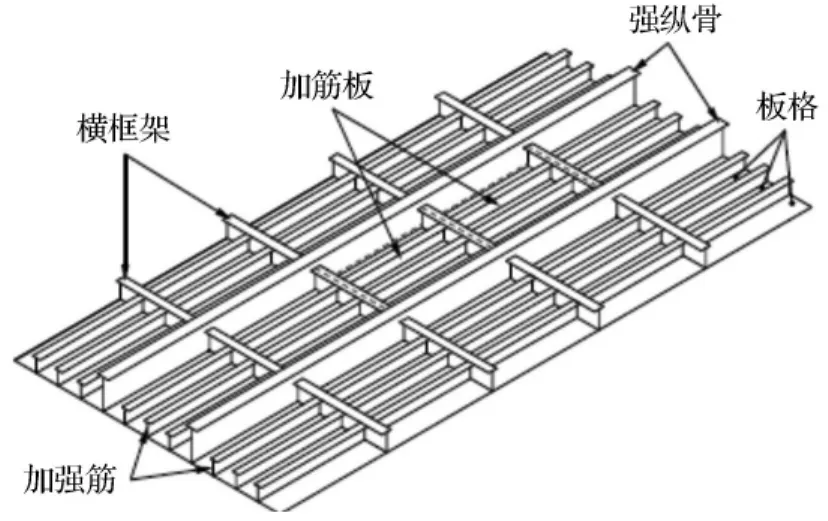
图1 船体板架结构

1.2 板格和加筋板模型的范围与边界条件

计算模型的范围和边界条件是相关联的，一般存在着单跨（one－bay）与双跨（1／2＋1＋1／2－bay）的选择.

单跨模型不考虑其对模型转动自由度的约束，四边均采取简支并在面内保持直线.为了在实际的设计中获得数学上的简化，此种模型和边界经常被采用.

双跨模型由于扩展了模型的尺寸范围，使得模型获得更加真实和客观的转动自由度约束.但对双跨模型来说，若加筋板的屈曲模态为奇数波型，则边界条件与单跨模型相同；若加筋板的屈曲模态为偶数波型，则应施加对称边界条件.

实际建模中为简化分析模型，一般不对支撑构件进行建模，其影响由施加自由度约束代替.本文对板格采取单跨模型，对于加筋板采取带四根加强筋的双跨模型为研究对象.

1.3 模型几何尺寸与材料属性及单元划分

板格 板格尺寸L×B×t＝4 300mm×815mm×14mm.

加筋板 板材L×B×t＝4 300mm×815mm×17.8mm；纵骨腹板hw×tw＝436mm×8mm；纵骨面板bf×tf＝172mm×17mm.

构件材料选用常见的船用钢材：E＝205.8 GPa，υ＝0.3，屈服强度бy＝315MPa.

单元尺寸的大小决定了模型网格的疏密程度.一般来讲，网格越密则模型越精细，能使得计算结果到更精确.但是在有限元非线性计算中，网格的疏密也很大程度上决定着计算时间，尤其是在带多根加强筋的加筋板极限强度计算中，更为明显.为了在计算时间与计算结果精确性之中达到平衡，在确定单元尺寸时有一个原则，即在单元的密度增加对计算结果影响微小，可认为上一步的单元尺寸已经合适.在本文中，经过多次计算比较和参考其他研究者的观点，采取以下单元尺寸方案：沿板格宽度方向取10个单元，沿腹板高度方向取6个单元，沿面板宽度方向取2个单元即可，沿板和加强筋纵向，根据单元形状尽量为正方形要求决定纵向单元尺寸.

1.4 初始变形的施加

现有的研究表明，光板和加筋板结构极限强度对初始挠度很敏感，所以在分析其极限强度的时候须将初始变形施加到结构中去.但是由于初始变形的形式相当复杂，如果手动进行加载初始变形是件非常困难的事情.解决的方法之一是编制扩展程序，将初始变形通过改变单元节点坐标来实现［5］.目前一般的处理方法是先计算结构的屈曲，将低阶屈曲模态以指定的变形幅值施加到计算模型中.虽然这种方法在计算结构的屈曲或极限强度时能大致计入初始变形的影响，但与实际结构的初始变形一般情况下并不一致，因此得到的结构的屈曲或极限强度结果将会出现偏差.

初始变形能够明显影响板和加筋板的极限强度特性，所以采取合适的方法去施加初始变形就显得很关键.

对于板格而言，只需考虑板自身的局部屈曲，本文中将板的初始缺陷与不同的加载形式相关联，通过提取第一阶模态，扩大到幅值Wopl＝B／200即可完成初始变形的施加.

对于加筋板，则复杂得多.本文考虑双向受压的加载情况.计入3种与屈曲相关联的初始缺陷，同时考虑加载方式对屈曲模态以及初始变形的影响.

1）与双向受压屈曲模态相关联的板的初始缺陷，幅值为B／200.

2）与双向受压屈曲模态相关联，梁柱型的筋的初始缺陷，幅值为L／1 000.

3）与双向受压屈曲模态相关联，筋的侧倾型的初始缺陷，幅值为L／1000.

在计算中，首先要进行特征值屈曲分析，而后据所得屈曲模态分别挑选出与以上3种初始变形形式相似的模态，使用Ansys中的Upgeom功能，分别挑选出与板和筋相关的节点进行单独的变形施加操作，最后将各部分扩大到所需幅值后，叠加在一起就完成了加筋板初始变形的施加.

显然，如何去挑选模态和计算者的判断有关系.本文在处理时遵循了以下原则：板和加强筋的模态首先要均匀分布，例如板上“峰”、“谷”分布要均匀，筋的模态也要均匀协调.在满足均匀性要求时，以倾向低阶模态为原则.选择低阶是因为模态较低的屈曲优先发生，进而达到屈曲所需的压力要小，从而使得所计算的极限强度值偏于安全.显然根据均匀性的要求，加筋板的初始缺陷并不是简单地锁定第一阶.

2 非线性有限元计算

2.1 板格和加筋板的复合受压载荷

选取以下4种载荷模式对板格进行计算，考虑双向轴压与侧压的复合作用，见表1.

表1 板格上双向轴压与侧压载荷

选取以下4种载荷模式进行计算，重点考虑不同轴向压力加载下的加筋板极限强度特性，见表2.

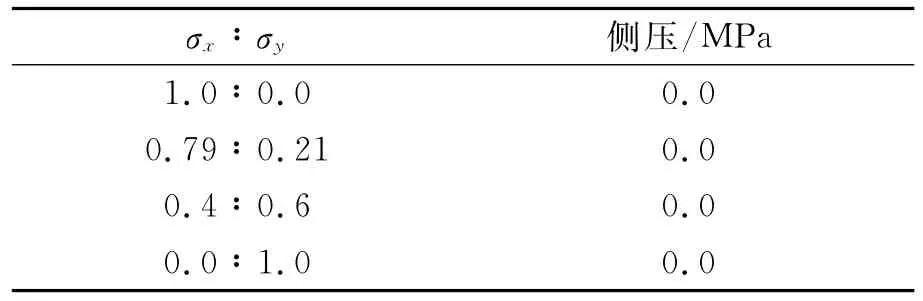
表2 加筋板上双向轴压与侧压载荷

其中板格的计算由于考虑到了侧压的作用，将导致在非线性计算中产生多载荷步的计算问题.本文在处理时先施加侧压，以得到在前一步进行特征值屈曲分析所获初始缺陷基础上的再次变形结果，而后施加轴向压力.

2.2 非线性有限元计算

板格及加筋板的有限元模型见图2～3，板格和加筋板的计算极限状态时的von Mises应力及应力与应变关系见图4～13.

图2 板格有限元模型

图3 加筋板有限元模型

图4 板格极限状态时的应力分布（σx∶σy＝1.0∶0.0）

图5 板格极限状态时的应力分布（σx∶σy＝0.8∶0.2）

图6 板格极限状态时的应力分布（σx∶σy＝0.7∶0.3）

图7 板格极限状态时的应力分布（σx∶σy＝0.5∶0.5）

图8 加筋板极限状态时的应力分布（σx∶σy＝1.0∶0.0）

图9 加筋板极限状态时的应力分布（σx∶σy＝0.79∶0.21）

图10 加筋板极限状态时的应力分布（σx∶σy＝0.4∶0.6）

图11 加筋板极限状态时的应力分布（σx∶σy＝0.0∶1.0）

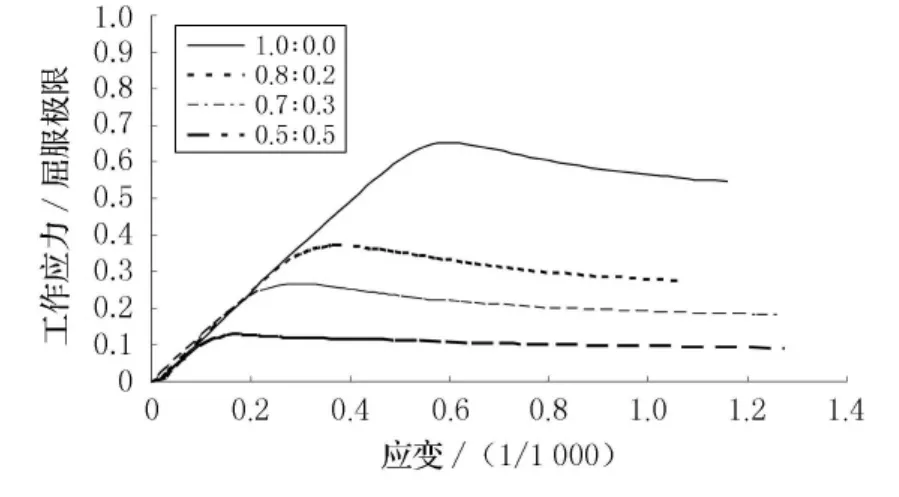
图12 板格的应力与应变关系曲线

图13 加筋板的应力与应变关系曲线

3 计算结果分析

现将本文所得计算值与文献［6－7］进行对比，结果见表3～4.其中计算值与参考值均为极限状态时刻工作应力与屈服强度的比值.

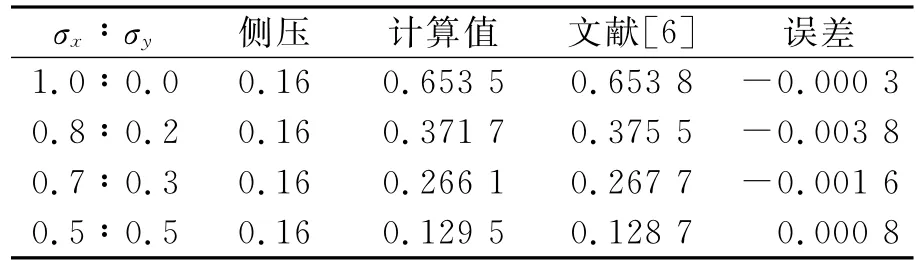
表3 板格计算值与文献值的比较

表4 加筋板计算值与文献值的比较

由表3可见，就板格而言，计算值与参考值之间误差很微小.由表4可见，对于加筋板来说，两者最大误差在5%左右，以加筋板的复杂程度来看，计算结果是可以接受的.

板格和加筋板的误差有此区别，是由于加筋板的初始缺陷的施加比板格复杂得多，还与计算者自己的判断有很大关系的原因.

4 结束语

本文分别对2块分别来源于实船结构的板格和加筋板进行了非线性有限元的极限强度计算，重点就两者计算模型的选取，边界条件的施加，以及初始变形的实现等方面进行了论述.

从计算所得的结果和已有的研究结果相比较可知，两者符合的比较好，证明了本文所采取的计算方法和处理方法是正确的，同时也佐证了Ansys作为一款功能强大的通用软件，其在进行极限强度非线性分析时的有效性.

本文极限强度的计算及处理方法可为结构非线性计算分析提供一定参考.

［1］Yao T，Astrup O C，Caridis P，et al.Ultimate hull girder strength：proc.of 14th international ship and offshore structures congress［C］.Nagasaki，Japan，2000，2：321－391.

［2］Simonsen B C，Estefen S F.Ultimate strength：proc.of 15th international ship and offshore structures congress［C］.San Diego，USA，2003，1：265－328.

［3］Yao T，Brunner E.Ultimate strength：proc.of 16th international ship and offshore structures congress［C］.Southampton，UK，2006（1）：353－438.

［4］Paik J K，Brunner E.Ultimate strength：proc.of 17th international ship and offshore structures con－gress［C］.Seoul，Korea，2009，1：375－474.

［5］Zhang S，Khan I.Buckling and ultimate capability of the plates and stiffened panels in anxial compression［J］.Marine Structures，2009（22）：791－808.

［6］Paik J K，Seo J K.Nonlinear finite element method models for ultimate strenth analysis of steel stiffenedplate structures under combined biaxial compression and lateral pressure actions—Part I：Plate elements［J］.Thin－walled Structures，2009（47）：1 008－1 017.

［7］Paik J K，Seo J K.Nonlinear finite element method models for ultimate strenth analysis of steel stiffenedplate structures under combined biaxial compression and lateral pressure actions—Part II：Stiffened panels［J］.Thin－walled Structures，2009（47）：998－1 017.