基于数据挖掘技术的电力网络参数估计方法研究
2012-06-17李吉德彭生刚王承民
李吉德,彭生刚,王承民
(1.长岛供电公司,山东 烟台 265812;2.平度供电公司,山东 青岛 266700;3.上海交通大学电子信息与电气工程学院,上海 200030)
0 引言
状态估计是能量管理系统(EMS)的重要组成部分,安全分析、经济运行等功能在很大程度上取决于状态估计所提供的估计值的正确性。而状态估计结果的正确性依赖于量测量的正确性、量测量的冗余度及正确的网络拓朴和网络参数。对于量测量的误差现有较多的方法解决,而且效果较好[1];而网络拓朴结构的错误一般会造成较明显错误的状态估计值,所以也比较容量辩识;但一般网络参数值误差较难发现,而且这种误差如不被发现的话,一直使用会使状态估计产生永远的误差。
导致给定参数值与实际值之间误差的原因通常为:1)有时因缺少实测参数量而直接采用设计参数或参数测量条件与实际运行条件差别较大,这都会使给定的参数值与实际运行中的元件参数有差别;2)实际运行中的元件参数因改线、改建,或因环境变化等原因而局部地、缓慢地发生着变化;3)调度中心对运行中的自动调压变压器的分接位置或补偿电容器的组数掌握得不一定确切。特别是输电线路,一般给定的参数值是在理想情况下的,但实际线路的情况与理想情况有时相差很大,因此一般给定的线路参数值和实际值相比大约有 25%~30%的误差[2]。
错误的参数值会造成以下结果:1)参数错误对所包含错误支路参数的状态估计量产生较大的误差,从而影响其它一些应用,如安全分析等;2)一些在正常范围内的测量值因与网络参数不一致而被检测成坏数据;3)长期的误差使运行部门对状态估计的结果失去信心;4)直接使用给定的参数值减弱了状态估计检测辩识坏数据的能力;5)功率分配不经济,特别是实施电力市场以后,在一些情况下可能增加交易成本,文献[2]举例说明了此种情况。
因此网络参数估计在电力系统分析中得到越来越多的关注,与状态估计和拓扑估计一样变得重要。研究这方面的文章较多[3-8],但对参数估计大致可以分为以下两种方法:1)基于残差和量测误差之间关系的灵敏度分析[3-4],这种基于灵敏度分析的状态估计与参数估计,采用一般的状态向量,在状态估计结束后再进行参数估计;2)基于增广矩阵的估计,又可以分为基于常规法方程的增广状态估计[5-6]和基于卡尔曼滤波的增广状态估计[7-8]两种。基于常规法方程的增广状态估计方法受权重影响较大,而且增加了估计的矢量,矩阵的行和列向量也得到了增加了,降低了计算效率,特别是应用于在线计算时,处理速度较慢。此方法适用于估计值为常量的参数。基于卡尔曼滤波的增广状态估计方法一般认为后一时刻的值等于前一时刻的估计值,但如果负荷变化比较快时,滤波的收敛性会较差,此方法适用于估计值随时间变化的参数。
上述两种方法的参数估计值与量测值的精确度有很大关系。如果量测量比较正确,那么估计的参数值精确度就会高于不估计的参数值;但如果参数值较为正确,而量测值误差较大,则会适得其反。而且如果与估计参数相关的量测量的误差没有检测出来的话,所得的参数估计值精确也较低。
数据挖掘技术也被称为数据库知识发现KDD(Knowledge Discovery in Database),主要目的是从大量的数据中抽取正确的、未知的、有价值的模式或规律等知识的复杂过程。数据挖掘所得到的知识虽因具体应用目的不同而有所不同,但总而言之是一种能够为人们用于辅助决策的知识。本文提出了一种基于数据挖掘技术的参数估计方法,利用SCADA系统所保存的大量历史量测数据进行分析,消除各种因素带来的误差。首先对历史数据进行了预处理,然后对预处理后的数据进行聚类分析,得到各个分类,之后把各个类的数据代入线性回归方程,就可用最小二乘法解出各种情况下的网络参数值。在应用的时候只要把实际量测的数据归入其中一类就可得到此种情况下的参数值,以供状态估计等所用。从预处理算法直至后期的回归算法都对大量的历史量测数据给予了充分的考虑,因而最后计算得到的参数估计值能够正确反映网络的实际情况。
1 样本选择
聚类分析是数据挖掘中一种十分重要的分析方法。所谓聚类是一个将数据集划分为若干组或类的过程,并使得同一组内的数据对象具有较高的相似度,而不同组中的数据对象则是不相似的。相似或不相似的度量是基于数据对象描述属性的值确定的。通常是利用(各对象间)距离进行描述的。
输电网络主要有两个设备的参数,一是输电线路的参数,另一是变压器的参数。输电线路的电导、电纳等参数主要受电流,周围温度以及风等几个因素影响,同时时间也是一个主要因素,这是因为随着时间的增长,线路会不断的老化,从而线路参数会不断发生变化。所以在进行数据挖掘过程中,如数据的保存时间太久的话一般就不作为挖掘的对象了。而变压器参数主要是变压器抽头的错误所带来的影响。所以在聚类分析时,线路参数分类主要依据周围环境、天气、温度及负荷水平等,而变压器参数分类则主要依据负荷水平和两端电压。在线路聚类分析中用到的数据矩阵的结构如下:

上式中Weather代表天气,Temp代表温度。变压器的矩阵结构形式和上式一样。
根据线路和变压器的数据矩阵结构,文章采用基于划分方法的聚类分析。基于划分的聚类算法就是把给定包含n个数据对象的数据库和所要形成的聚类个数K,划分算法将对象集合划分为K份(K<n),其中,每个划分代表一个聚类。所形成的聚类将使得邇客观划分标准(常称为相似函数,如:距离)最优化,从而使得一个聚类中的对象是“相似”的,而不同聚类中的对象是“不相似”的。
划分方法采用k-means算法。此算法的步骤如下:
①初始化。确定分组的个数K,在样本空间中选择K个点,称为种子,这些种子构成初始聚类中心,它们之间应该有足够的距离用于改善算法的收敛性。一般要求选出的K个观测数据(种子)间距离的倒数大于给定的阀值,而且它们的距离应该大于它们与观测数据的聚类的距离。一旦形成了种子,就形成了观测数据的初始划分,将观测数据分到离中心较近的组中。
②转移评价:计算每个观测数据到K个聚类中心的距离,观察数据和被分配到组间中心的距离应最小。如果不是最小,观察数据就应该被分到另一个离它最近的组中,再次计算旧组和新组的聚类中心。
③循环:重复步骤2,直到得到一个较为稳定的分组。
为了计算观测数据和组中心的距离,k-means算法采用了欧式距离,在第t步的迭代中,第i个观测数据和第l个聚类中心的距离等于
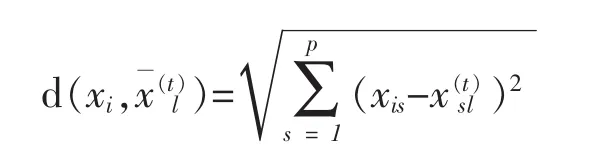
i=1,2…n;l=1,2…K
此方法的一个缺点就是如何确定K的数值。K太多了会影响每次搜索类的时间,增加了计算时间,实时性就会比较差;K太少了又不能正确反映网络参数的真值。
2 数据处理
在进行数据挖掘以前,首先要进行数据的处理。因为对于大量的数据,肯定会存在不完整、含噪声和不一致的数据,而如果不对这些数据处理,会影响数据挖掘所获模式知识的质量。
2.1 空缺值的处理
由SCADA所提供的量测数据中,因通信通道问题,或量测装置问题,肯定会有一部分量测量是没有传送到调度中心的;或送到了数据库,但没有保存到数据库。所有这些造成了数据的缺失。对于数据缺失值的处理,应尽可能的利用其同一时段其它所采集到的数据来进行填补。
文章采用rough理论的ROUSTIDA算法来进行补全缺失值。ROUSTIDA基本思想是:缺失数据值的填补应使完整化的信息系统产生的分类规则具有尽可能高的支持度,产生的规则尽量集中。该算法的目标是使具有缺失值的对象和信息系统的其他相似对象的属性值尽可能保持一致,并尽可能使属性值之间的差异最小。
具体算法的实现:可辨识矩阵反映了对象间的属性差异,因此利用可辨识矩阵作为算法的基础,是一种很自然的想法。由于不完备信息系统中存在多个属性值和其不同的分布,因此对信息系统遗失数据值的填补不是通过对初始可辨识矩阵的一次运算并加以完整化分析就能对所有的遗失值进行补齐;实际上要经过多次对扩充差异矩阵的计算和完整化分析,直至终止条件成立。为此,设初始信息系统为S0,对象集为,相应的可辨识矩阵为M0,xi的遗失属性集为,无差别对象集为;第r次完整化分析后的信息系统为Sr,对象集为,相应的可辨识矩阵为 Mr,xi的遗失属性集为,无差别对象集为,完整化分析所依赖可辨识矩阵计算,具体过程如下:设Mr+1=[Mr+1(i,j)]n×n],r=0,1,2…,则 Mr+1(i,j)计算如下:
这样就可以把缺失值以最有可能值来进行填补。
2.2 异常点的判断处理
异常点就是与数据库中的大部分数值有很大的不同或不一致。对于异常数据,采用基于距离的检测方法。基于距离的基本思想:如果样本S中至少有一部分数量为p的样本到Si的距离比d大,那么样本Si是数据集S中的一个异常样本。判断的标准建立在两个参数p、d的基础上,两个参数的值可根据数据的相关知识来确定。文章把5个采样断面作为一组,因此把p设为3,d值则随功率,电压的不同而选择,一般线路功率 d值不超过线路所传输功率的20%左右,电压d值一般是线路额定电压的10%左右。如果在此组数据中检测到异常值,则此异常值用另外几个数据的平均值来替换。
2.3 数据的替换
对于每次采集的数据,进行完数据处理以后,就保存于数据库。但是实际运行中的元件参数因时间的变化会缓慢的发生变化。因此在进行数据挖掘时,数据间的时间间隔不能太长。因此每次存入新的采集数据时,把距此次数据时间间隔最长的那批数据替换掉,以保证数据库中的数据能反映最近的网络实况。
3 基于线性回归方法的参数估计
在聚类分析完成以后,可得到按照天气、温度与负荷水平等划分的各个类别的样本数据。把各类的大量数据代入线性回归方程就可以计算不同天气、温度与负荷水平等条件下的网络的参数值。
3.1 多元线性回归方程
多元线性回归方程的表达式:
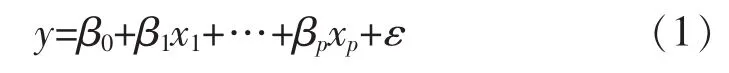
其中ε是服从正态分布N(0,σ2)的随机变量。
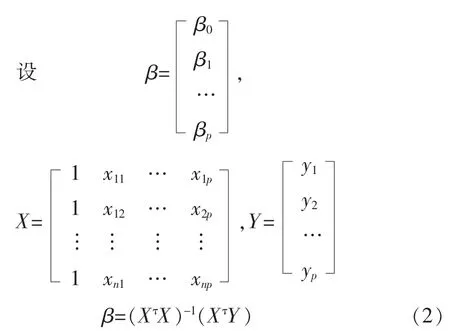
其中β是回归系统,它是一个无偏估计,β的协方差矩阵等于 ∂2C,其中 C=(XτX)-1,Xτ为 X 的转置矩阵。
由于β是无偏估计,所以利用大量的数据进行计算,可降低β的误差,当数据足够多的时候,误差将会趋向于零。
3.2 线路参数的回归方程
输电线路的潮流方程如下:
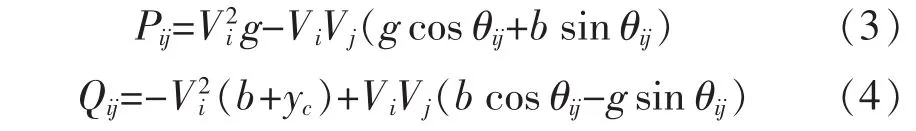
式中Pij、Qij分别代表线路ij的始端有功、无功功率,其方向规定:由i流向j为正,由j流向i为负。
把(1)和(2)式右边的第一项移到左边后两边平方:

把(7)式展开合并移项以后得到如下式子:
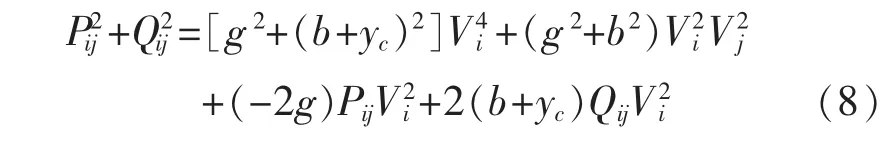
其中 Pij、Qij、Vi、Vj为量测量,并对(8)式进行如下的变量代换
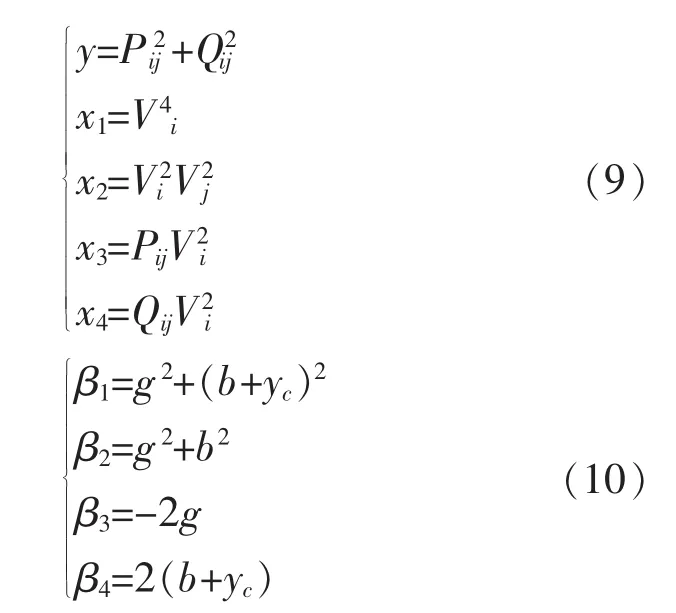
(8)式就变换成如下的等式:

其中β0=0,(11)式就是一个线性回归方程,把上面聚类分析所得到的各个类的数据代入(9),由(2)式就可以求得各个类所对应的 β1、β2、β3、β4。 在(10)式中,有三个变量,四个等式,因此可用最小二乘法求取参数g、b、yc的估计值。
3.3 变压器参数的回归方程
变压器支路的潮流方程如下
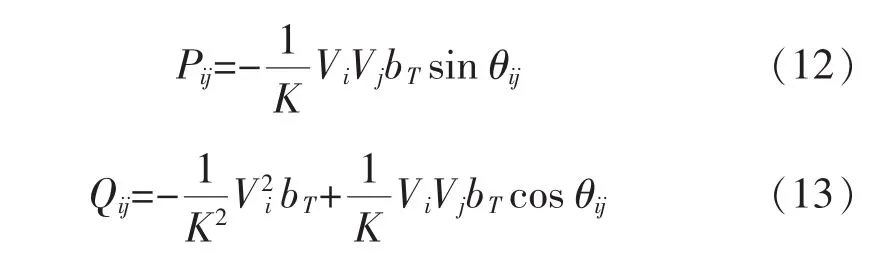
式中:K为变压器非标准变比;j为标准侧,变比为1;i为非标准侧,变比为K;bT为变压器标准侧(j侧)的电纳。
求取参数K、bT的方法和求取线路参数的方法一样,其中
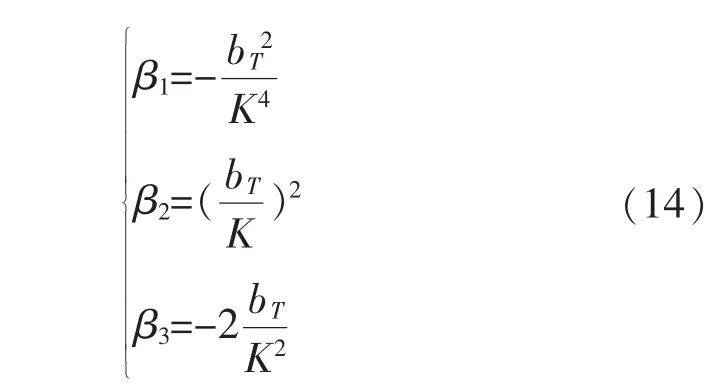
同样在求得 β1、β2、β3以后,用最小二乘法就可以得到变压器参数K、bT的估计值,求得K以后还要计算出K最接近的分接头的变比。
4 讨论
虽然基于划分聚类分析的结果是全局最优的,但此划分是根据量测量来划分的,而文章所要求的是网络参数值,所以最后用最小二乘法所求得的网络参数值,可能前后两个类之间的值相差比较大,特别是输电线路的电阻值。在这种情况下,我们对前后两个类之间所求得的值设定一个阀值,如果前后两个类之间的参数值超出此阀值,就重新进行聚类的划分,以保证前后两个类之间的参数差值小于给定的阀值。
各个类的参数值计算都是采用离线计算,这就增加了此方法的实用性,可用于任何规模的电力网络,不用考虑有些算法要实时计算时速率问题。
在计算得到网络的各个参数值以后,最后还要对此方法进行验证。验证所用的数据可以从数据库中提取三分之一左右。但不用每次计算时都要验证,可采取隔几天或者运行环境变化较大时才重新验证。
对于每次状态估计所用的网络参数值,通过所采集的数据来搜索所对应类的网络参数实际值。但如整个网络的拓朴没有发生变化,而且线路的负荷水平变化也不大时,可以考虑得用前一次所得的参数值作为本次状态估计用的值,这样可以节省搜索的时间。因每条线路与变压器都是单独并列计算的,如变压器分接头发生动作时,而其它不变时,只搜索发生动作变压器的类。

表1 30个样本参数计算结果

表2 100个样本参数计算结果
5 算例分析
采用文献[9]中的四节点系统来验证此方法。因系统缺少实际运行所要采集的数据,所以所用的量测值也是在文献已经计算的结果基础上加一正态分布的随机误差来产生,从而不考虑其它一些如周围环境,天气温度等因素。文章分别列举了30与100次量测样本的全部计算值(表1、表2)。同时为了对比说明本方法的效果,与文献中用增广矩阵所计算的参数估计值作了比较。
从表1、表2可以看出,当样本数量达到一定数量以后,参数计算值与真值相差不多了。图1说明了参数b13随着样本数量的逐渐增加,相对误差越来越小,其他参数也具有同样的性质。
通过对此系统的成功测试,将此方法应用于一个实际系统中,来求取此系统在各个情况下的参数值,以供状态估计及其它能量管理系统(EMS)中的程序所用。并且通过计算出系统的实际值,为用户创造了较大的经济效益。直接采用数据库中所给的数据,在有些情况下运行人员认为线路的输电能力没有达到负荷极限,但其实已经达到了负荷极限,从而使得线路长时间处于过负荷运行,可能造成线路的断裂;或者认为线路的输电能力已经达到了极限,其实还没有,特别是在缺电的情况下,从而也造成一些不必要的损失。
由于方法采用离线的计算,所以在计算速度方面没有太大的要求。为了能够求得在各种情况下网络参数的真值,数据容量为一年各个时间段的数据。通过对所用的数据进行聚类分析,得到各个类,温度和负荷水平是分类的主要判据。把各个类中的数据代入公式,发现计算出来的参数值前后相差有时较大。表3列出了计算所得的各个参数值与所给定的参数值之间的统计表。
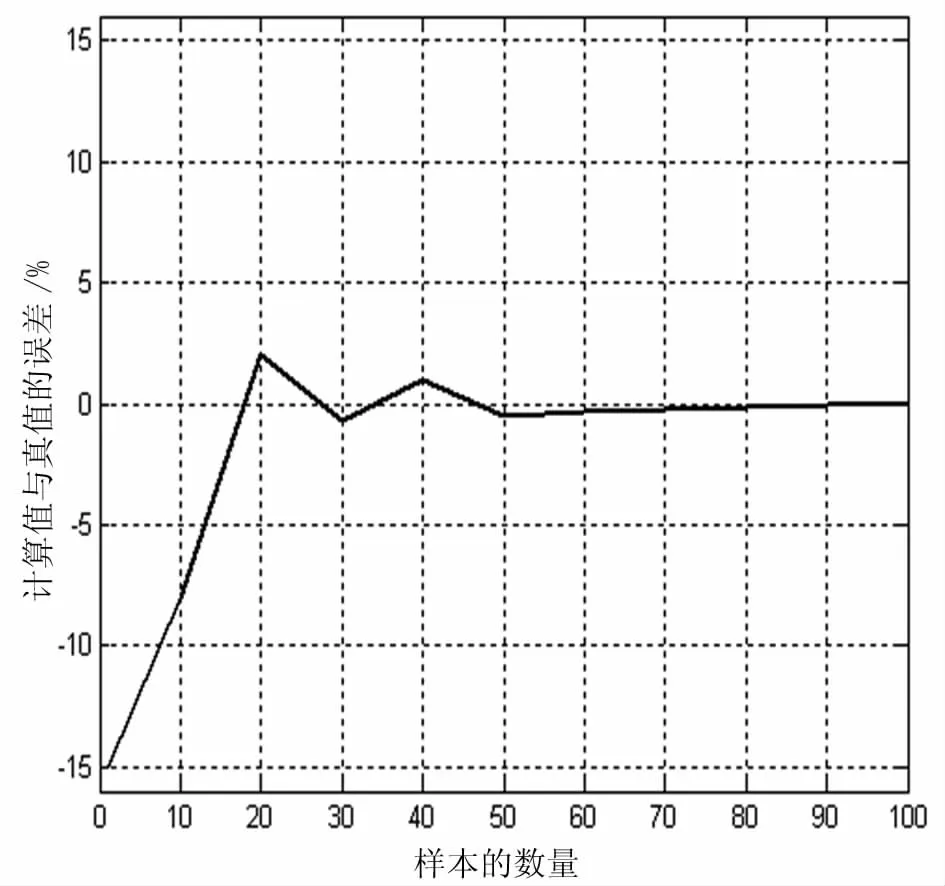
图1 不同样本容量和计算误差之间的关系
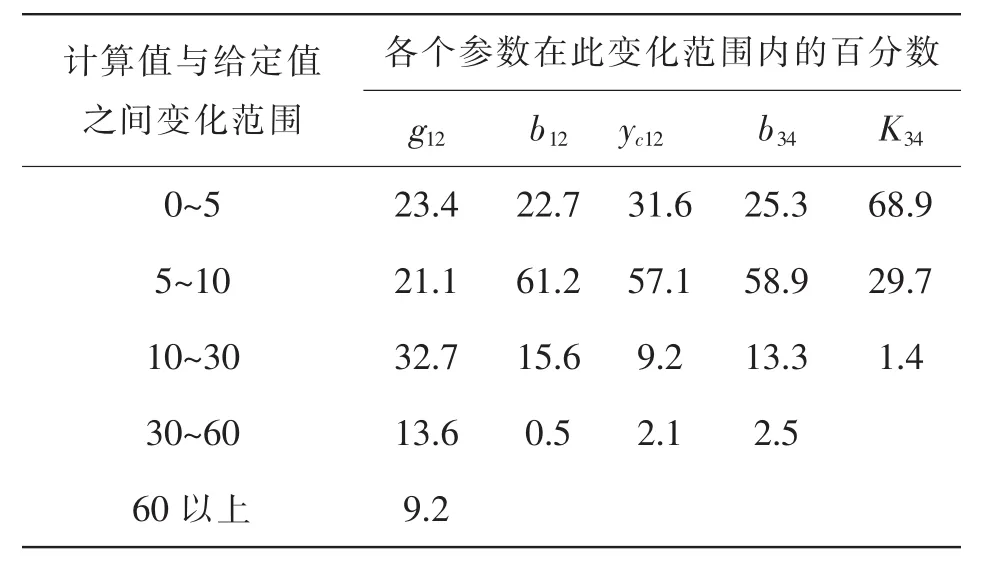
表3 计算值同给定值的关系
6 结论
正确的网络参数值对于电力系统分析越来越重要,但如果参数值错误的话,会对状态估计、优化运行,安全分析等的结果产生较大的影响,特别是实施电力市场以后,对参数值正确性的要求越来越高。
针对得要到一个正确反映网络在各种情况下的参数值比较困难的问题,文章提出了一种基于对大量历史数据进行挖掘计算参数值的方法,能过聚类分析,把历史数据分成各个类。因每个类都有大量的历史数据来反映网络情况,所以最后的网络参数值能够代表各种情况下的正确值。
最后的两个算例表明所提出的基于数据挖掘技术的网络参数估计正确性比较高,实用性比较强,可靠性比较高。
