铅芯橡胶支座调谐质量系统减震效果
2012-06-15李志平田杰芳袁晶晶葛楠
李志平,田杰芳,袁晶晶,葛楠
(1.河北联合大学 建筑工程学院,河北 唐山 063009;2.唐山学院,河北 唐山 063000)
0 引言
调谐质量减震装置(TMD)实际上是一种吸能减振装置,最早应用于机械减振和降低噪声,最近被应用于控制结构的地震和风振反应,属于被动控制。作为调谐减震控制系统中的核心部件,TMD是附加在主结构中的一个子结构,由质量块、弹簧、阻尼器组成。质量块通过弹簧(连接件)和阻尼器(耗能减震装置)与主结构连结在一起,一般支撑或悬挂在主结构上。质量块的存在使原结构产生了附加的质量、刚度和阻尼,通过子结构的这些基本特性调谐其自振频率,可以使其尽量接近主结构控制振型的振动频率。这样,当结构在外激励作用下产生振动时,主结构带动TMD系统一起振动,TMD系统相对运动产生的惯性力反作用到结构上,对结构的振动产生控制,TMD系统中的阻尼器也将发挥耗能作用,从而达到减小结构振动反应的目的。
TMD技术主要应用在层数较多,高度较大,主振型变化明显与稳定的多层、高层、超高层建筑以及大跨度桥梁、塔架、高耸结构等。TMD装置减振机理明确,已取得较多的理论研究和实验研究成果,并在一些工程中得到应用,总体上还处于不断发展的阶段,表现为以下几个特点:
(1)只能控制一个或有限几个振型(视质量调谐装置数量而定)。对主振型不明显、不稳定的结构的减振效果仍没有统一定论。
(2)减振效果要通过充分的理论论证和大比例尺震动台模型试验验证。
(3)调谐系统装置制作安装要简单。
由于铅锌橡胶支座(LRB)减震装置具有非常大的竖向刚度,同时钢板又不影响橡胶板的剪切变形,因而保持了橡胶固有的柔韧性,为支座提供了水平向柔性和自复位能力,结构的自振周期明显延长。设想在结构的顶部设置LRB装置,使调谐附加质量具有一定的质量,就可以起到调谐质量阻尼器的作用。本文以拉格朗日方程为基础建立了结构顶部采用LRB调谐质量系统的运动方程,用基于MATLAB编程的Newmark-β数值分析方法,分析了调谐质量阻尼器的减振效果。
1 铅锌橡胶支座(LRB)的构造和减震系统模型
铅芯橡胶支座是在板式橡胶支座的基础上,在支座中间加入铅芯以改善支座阻尼性能的一种减震支座。如图1所示,铅芯橡胶支座由用来支承荷载的层状橡胶、钢板及用于吸收耗散能量的铅芯组合而成,上下连接板,使橡胶垫与上下结构(构件)可靠联结。
在建筑结构的顶部设置LRB调谐质量减震系统的结构模型如图2所示,实际应用时需要在顶部设置多个LRB支座支撑调谐质量,由于每个支座的运动状态时一样的,因此可将多个支座合并成一个来考虑。

2 系统运动方程的建立
将结构简化成n个自由度系统模型,各个楼层质点的质量为mi,层间刚度系数与阻尼系数分别为ki和ci,调谐质量(块体质量)为m0,铅锌橡胶支座的刚度和阻尼分别为k0和c0。
根据拉格朗日方程建立LRB调谐质量系统的运动方程。拉格朗日方程形式如下:

其中:T是整个系统的动能,V整个系统的势能,是与xi对应的非保守广义力。
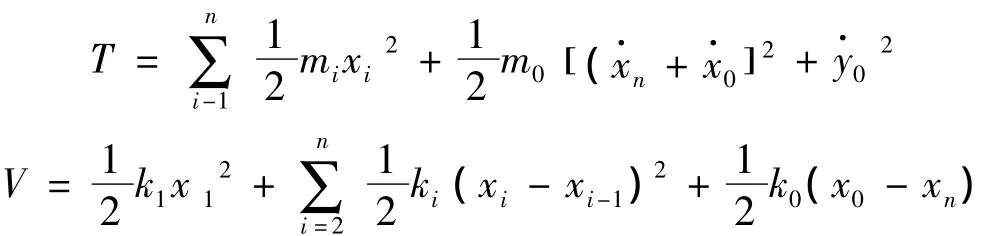
在计算广义力Qxi时,先让系统的广义坐标发生虚位移δxi,由虚功δA与δxi之间的关系确定Qxi,即虚功δA中,δxi和前面的系数表达式就分别为Qxi。当系统发生虚位移δxi时,参与做功的非保守力有地震力,即:

因此有:

将T、V、Qxi分别代入到(1),(2)式中,经整理后得到关于xi的运动方程为:
对于x1~xn-1有:

对于xn和x0有:
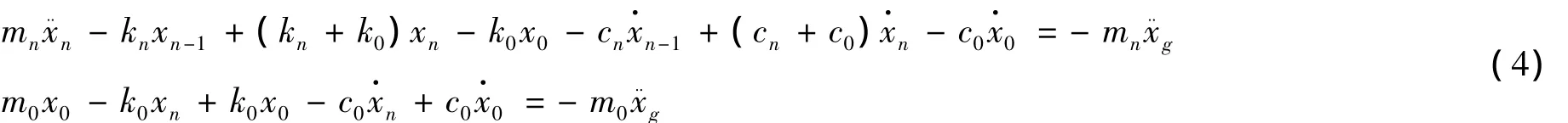
上述(3)、(4)两式是关于x1~xn-1及xn、x0的线性的二阶常微分方程组,可采用Newmark-β方法求解。
3 计算实例与结果
为了进一步考察LRB调谐质量系统的减振效果,取一个6层建筑结构,简化成一个6个集中质量的多自由度系统,mi=933 t,水平层间刚度系数ki=950 000 kN/m,水平阻尼系数ci=3 000 kN/m.s;在结构顶部设置LRB调谐质量减振系统,输入地震波为Elcentro波。最大水平地面加速度为3.40 m.s-2,地震烈度相当于8度。地震动力反应计算结果如表1、表2及图3~10。
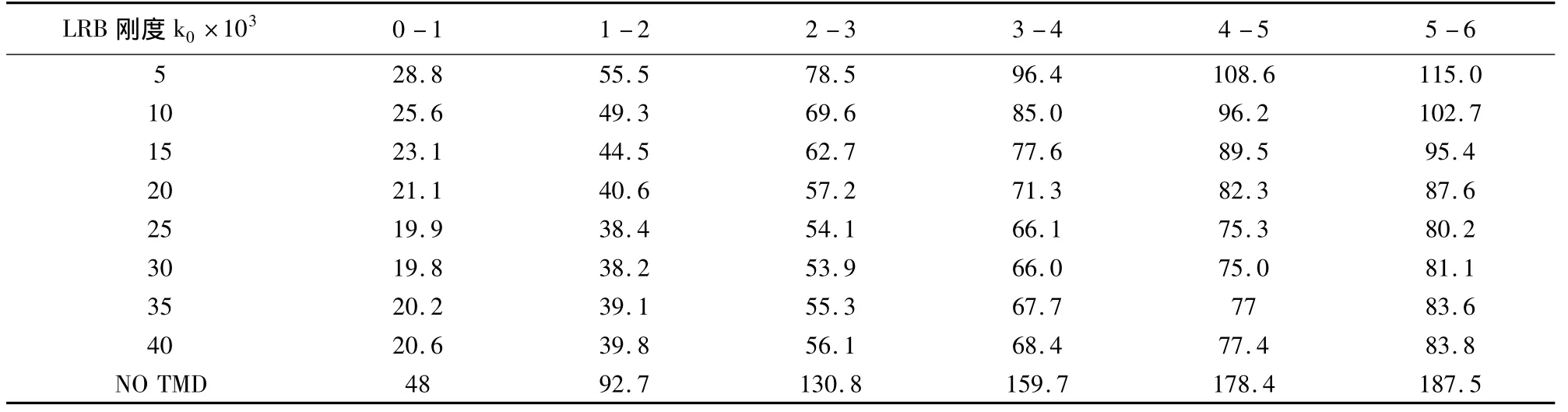
表1 LRB刚度与楼层位移(mm)(M=933 t,c0=2000)

表2 LRB刚度与层间位移(mm)(M=933 t,c0=2000)

表3 LRB阻尼系数与层间位移(mm)(M=933 t,k0=30×103)

表4 调谐质量与层间位移(mm)(k0=30×103,c0=3000)


4 计算结果分析
从图3及图4中可以看出,当LRB刚度k0为5×103kN/m时,阻尼器的位移时程曲线与速度时程曲线受到的影响已经非常明显;而且计算结果表明,当LRB刚度增加到30×103kN/m时,这时调谐质量系统减震效果最佳。
图5~图10反映了各项因素对调谐质量系统减振效果的影响。从图5及图6中可以看出,当LRB刚度k0在25×103~30×103kN/m范围以内时,减振效果最佳,因为最大楼层位移与最大层间位移均有明显的减少。楼层位移是绝对位移,层间位移是相邻楼层的位移差,结构的内力与层间位移直接相关。因此在这里主要分析层间位移的变化规律。从表2及图6中可以看出,当k0=30×103kN/m时,从第1层至第6层的减振效果为55.8% ~27.8%,效果明显。从图7及图8中可以看出,当k0=5×103kN/m时,各楼层的速度及加速度都有所减少,这对于结构本身及内部置放物都是有利的。从图9中可以看出,阻尼系数对减振效果有明显的影响。当500<c0<3000 kN/m.s时,所有楼层的层间位移随着阻尼系数的增加而减少;当c0=3000 kN/m.s时,层间位移达到最小值,减振效果最佳;当c0>3000 kN/m.s时,层间位移随着阻尼系数的增加而增加。
从图10可以看出,调谐质量M对减振效果也有明显的影响,总的趋势是M越大减振效果越好;但是当M/m>1.0之后,若M再增大,减振效果的增大并不明显。当M/m>1.4时,随着M的增大减振效果不再增大,因此可以认为M/m=1.4时即可达到最佳减振效果,不必设置更大的调谐质量。实际应用时应至少要求M/m=1.0才能接近最佳效果。
TMD调谐质量系统的减振效果还与结构的层数、层间刚度系数及各楼层质量分布有关,设计计算时应针对具体的结构进行分析计算。
5 结论
(1)以拉格朗日方程为基础建立了结构顶部采用LRB调谐质量系统的运动方程,用基于MATLAB编程的Newmark-β数值分析方法对运动方程求解可以得出合理的计算结果。
(2)LRB调谐质量系统具有明显的减震效果,但减振效果与LRB的刚度、阻尼系数,调谐质量有关,当k0=30×103kN/m,c0=3000 kN/m.s,M/m >1.0时,减振效果最佳。
(3)结构顶部设置LRB调谐质量装置的减振效果很明显,安装方便,接触面承受的荷载小,更换、维修容易。
[1]周锡元,阎维明,杨润林.建筑结构的震动、减振和振动控制[J].建筑结构学报,2002,23(2):2-11.
[2]唐家祥.建筑隔震与消能减震设计[J].建筑科学,2002(1):21-27.
[3]周福霖.消能、减振和结构控制技术的发展和运用[J].世界地震工程,1989(4),16-20.
[4]Wirsching P H,Yao JTP.Safety design concept for seismic structures.Comput Strucut,1973,3:809-826.
[5]Sladek J R,Klinger R E.Effect of tuned-mass dampers on seismic response.J Struct Div,1983,109:2004-2009.
[6]Villaverde R,Martin S C.Passive seismic control of cable-stayed bridges with damped resonantappendages.Earthquake Engineering and Structural Dynamics,1995,24:233-246.
[7]Lin C C,Ueng J M,Huang T C.Seismic response redunction of irregular building s using passive tuned mass dampers.Engineering Structures,1999,22:513-524.
[8]李春样等.质量阻尼器的发展[J].力学进展.2003.339(2):194-206.
[9]何明胜,石桂菊,张红彬,刘成刚.调谐质量减震技术及其应用前景[J].石河子大学学报,2010,28(5):618-624.
[10]Carotti A,Turci E.A tuning criterion for the inertial tuned damper.Design using phasors inArgand-Gauss plane.Applied Mathematical Modelling,1999,23:199-217.
[11]吴彬,庄军生.铅芯橡胶支座力学性能及其在桥梁工程中减隔震应用研究[J].中国铁道科学,2004,8(25).
[12]刘文光.橡胶隔震支座力学性能及隔振结构地震反应分析[D].北京工业大学,2003.
[13]谢军龙,周福霖.多层房屋结构TMD“加层减震”试验研究和应用[J].世界地震工程,1998,14(4):57-60.
