插入式静电传感器空间滤波法流速测量

阚 哲，邵富群，李庆华

(1.辽宁石油化工大学职业技术学院，辽宁 抚顺113001;2.东北大学信息科学与工程学院，沈阳110004;3.中国石油辽阳石化分公司，辽宁辽阳111003)

测量气/固两相流的流速是一项重要而又具有一定挑战性的工作，在煤粉燃烧过程，准确测量和控制煤粉流量，对改善环境和提高效率都是有推动作用的。利用静电感应原理测量气/固两相流参数的传感器大致分为两种:非接触式和插入式两种。非接触式静电传感器主要为圆环型，而且许多学者［1－4］正在致力于环型静电传感器的研究，目的是测量气/固两相流的速度［5－6］和质量流率参数［7－8］。然而环型静电传感器安装较复杂，需要隔离层和屏蔽层。插入式电极可以直接安装在传送管壁上，方便，快捷，也可在线测量气/固两相流参数。而且插入式静电传感器可以用于较大管径的传送管道［9－10］。

插入式静电传感器示意图如图1所示，其半径为R。本文在对插入式静电传感器的点电荷数学模型进行探讨的基础上，推导出了感应电极空间滤波测速原理，并进行了实验验证。

图1 插入式静电传感器示意图

1 点电荷数学模型

将单个带电固体颗粒看成点电荷，带电量为q1的点电荷数学模型几何示意图如图2所示。

图2 点电荷数学模型几何图

在图2中，L表示感应电极长度;x表示感应电极最大测量范围，R表示静电传感器电极的半径。具体计算过程如下:

C点电场强度E:

面元ds为:

利用高斯公式可计算出静电感应电极上的感应电荷q，有:

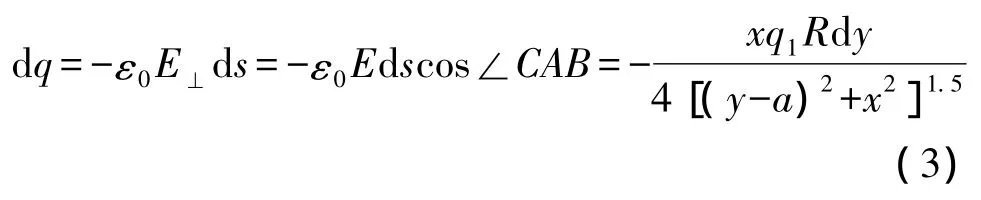
对y积分，得:

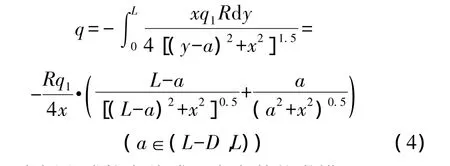
式(4)为插入式静电传感器点电荷数学模型。

2 空间滤波测速原理

2.1 空间滤波原理

基于推导得到的插入式静电传感器的点电荷数学模型(传送管中点电荷的位置不定)，利用传输系统的传递函数不变性，可以令点电荷位于传送管中心轴线上，即a=0时，将点电荷数学模型简化。利用输出感应电荷来推导插入式静电传感器的幅频响应。

将a=0代入式(4)得到点电荷数学模型的简化形式:

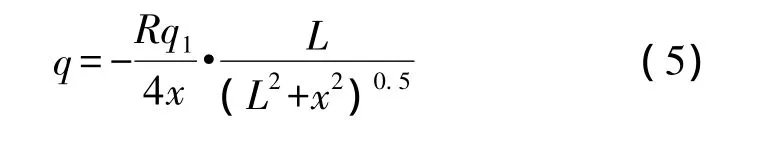
测量区大小为2x，表示固相颗粒在这个区域内，就将在插入式静电传感器上感应出电荷，即产生输出信号。

K表示比例系数。

令输入点电荷为:

点电荷在测量区2x内运行时间为2x/v。点电荷在测量区2x运行符合门函数［11］，其门函数具体如图3所示。

图3 点电荷在测量区内门函数

取拉氏变换，得系统函数:

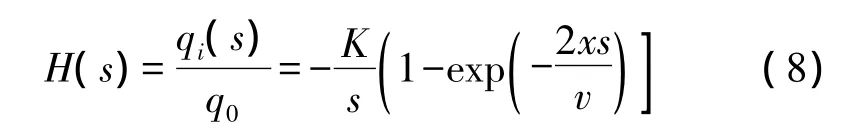
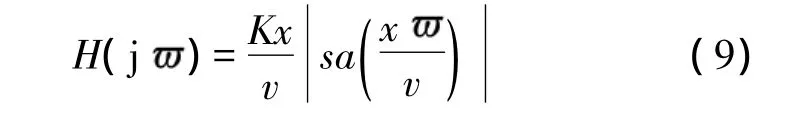
令 K1=Kx/v，式(9)化为

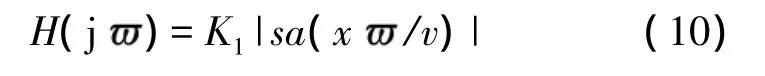
K1表示比例系数。

2.2 空间滤波特性

当不同颗粒经过电极的测量区时，颗粒形成的静电场如图4所示。在测量区内，每个带电颗粒只能在电极上某一面积感应电荷，如果将电极正对电荷的部分称为正面，那颗粒只能在电极正面产生感应电荷。颗粒静电场在电极上感应的静电荷区域好比人眼观察事物，只能看到某一物体的一面。对于图4中的q，q1，q2和q3在电极上感应电荷的区域近似相等，这样当带电颗粒(数学模型中作为点电荷)经过测量区时，电极对带电颗粒时刻起到空间滤波作用，有效空间滤波长度为2R。

由点电荷数学模型得到电极的幅频响应，其图像如图5所示。由于电极的幅频响应是电极本身特有的属性，不会随输入信号的改变而改变，这样插入式静电传感器就对输入信号起到滤波作用。

对于幅频响应幅值为零的点，

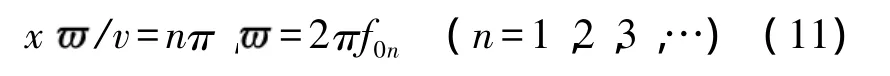
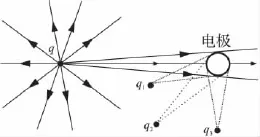
图4 点电荷在电极附近的电场

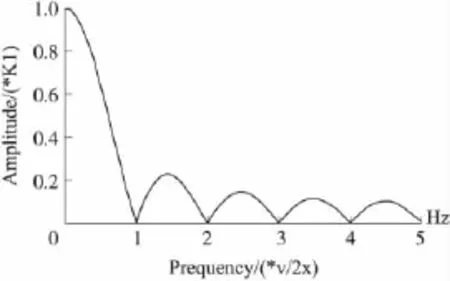
图5 感应电极幅频响应

当n=1时，得到频率和速度的表达式为:

2.3 空间滤波测速原理

通过对点电荷幅频响应分析得到输出随机电压信号频率与气/固两相流速度存在一定的关系，利用校正因子可以建立各点频率与速度的关系式。从图5中可以发现电压信号具有的特征频率为当幅值为最大时的频率，这样可以建立峰幅频率与速度的表达式［12－14］。

根据式(12)，令x=K2b，得到空间滤波法测量气/固两相流速度与第一个零幅频率的表达式。即

取校正因子为K3，截止频率为fc。这样就得到信号截止频率与速度的公式。即

K2表示比例系数。

K1对空间滤波测量速度原理没有影响，这样式(14)测速原理仅需要考虑比例系数K2和校正因子K3的影响因素。

2.4 获得截止频率fc的方法

静电传感器输出的信号带宽为2 kHz，但是当对测量信号进行FFT变换时，截止频率fc是较困难准确获取的。针对这一困难，采用“3 dB”原则来获取fc，进而完成插入式静电传感器的空间滤波测速。

“3 dB”原则:

由式(15)，在正确选取Pref或者Uref后，就可以得到测量信号的截止频率fc。

Px/Ux是截止频率处的功率/电压;Pref/Uref是计算截止频率时的参考功率/电压。

3 实验验证

插入式静电传感器如图6所示，其由金属屏蔽管和不锈钢电极构成。金属屏蔽管直径D=140 mm，电极长度L=70 mm，电极半径R=2.5 mm。静电感应信号经模拟放大模块放大，由数字采样模块进行计算和显示。实验验证电极空间滤波测速原理过程，采用细沙(粒径为0.5 mm)为测量对象，让细沙从漏斗中以不同高度自由流经感应电极。图7为细沙分别从漏斗距电极高度h=1 000 mm，h=1 500 mm和h=2 000 mm处自由落入传送管道时，感应电极测量得到的信号图形，并分别进行了FFT变换。观察图7可以明显看到当流体流过电极的速度不同时，测量所得信号的频域图d、e和f有明显的变化，而且随流速的增大信号带宽变宽，这可靠的说明了插入式电极对测量信号有空间滤波作用。

图6 插入式静电传感器

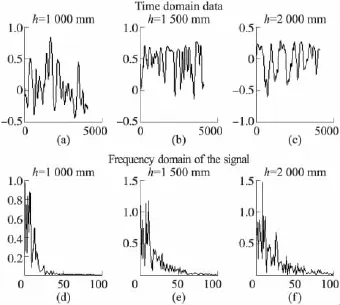
图7 连续流动颗粒输出电压频域波形

为验证插入式静电传感器空间滤波测速的重复性误差，选择沙子(粗细两种)和氧化铝粉沫两种物料进行实验。在h=500 mm时，对不同的物料完成了一些列实验，其固相速度测量结果如图8所示。图8中为测量得到的物料速度(流经插入式电极时)，采用了粒径为 0.1 mm，0.5 mm 的沙子和 0.5 mm氧化铝粉沫作为实验测量对象。

图8 不同物料时空间滤波测量速度

观察图8，可以得到:对于同种物料沙子而言，粒径大对测量结果有较大影响，而且速度值要大于细沙时的测量结果;对于不同物料而言，氧化铝粉沫测量结果波动较大，而从粒径方面看，氧化铝粉沫与粗沙的测量结果相一致，均对速度测量结果产生了较大波动;细沙测量结果相对较好，波动比较小，出现了较好的测量重复性。而此测量流体速度的方法重复性误差小于±10%。

采用插入式静电传感器空间滤波测速方法完成不同流体速度测量实验，现取h=200 mm，h=500 mm，h=1 000 mm，h=1 500 mm 和 h=2 000 mm 从漏斗落入传送管道，利用式(14)来测量流体速度。采用“3 dB”原则获取信号的截止频率，取表达式中的2K2K3R=0.844 5，测量得到的流体速度与自由落体速度如图9所示(重力加速度gn=9.8 m/s2)。

图9 自由落体速度和空间滤波速度

图9中利用电极空间滤波测速原理得到的速度，均比自由落体速度小，这可以通过校正因子进行调整。图9中空间滤波速度的趋势线也很好的说明了图7中信号带宽的变化规律，进一步证实了插入式静电传感器的空间滤波原理。

4 结论

根据静电感应原理，由插入式静电传感器点电荷的数学模型和幅频响应的不变性，推导得到了电极的空间滤波测速原理。采用“3 dB”原理获取信号的截止频率，结合实验验证了插入式静电传感器的空间滤波原理，其速度测量重复性误差在±10%以内。插入式静电传感器空间滤波测速法在测量的过程中，需要选用一种标定办法。本研究过程中选用的是环状静电传感器相关测速办法来标定插入式电极测量得到的速度。

［1］ Gajewski J B.Continuous Non-Contact Measurement of Electric Charges of Solid Particles in Pipes of Pneumatic Transport［J］.PartⅠ:Physical and Mathematical Models of a Method，IEEE/ISA Annual Meeting，1989:1958－1963.

［2］ Yan Y，Byrne B，Coulthard J.Sensing Field Homogeneity in Mass Flow Rate Measurement of Pneumatically Conveyed Solids［J］.Flow Measurement and Instrument，1995(2):115－119.

［3］ Armour-Chélu D I，Woodhead S R.Comparison of the Electric Charging Properties of Particulate Materials in Gas-Solids Flows in Pipelines［J］.Journal of Electrostatics，2002(56):87－101.

［4］ Coulthard J，Cheng R X，Keech R.Developments in Pulverized Fuel Metering for Coal-Fired Power Stations［J］.Power Engineering，2000:100－104.

［5］ Yan Y，Byrne B，Woodhead S R，et al.Velocity Measurement of Pneumatically Conveyed Solids Using Electrodynamic Sensors［J］.Measurement Science ＆ Technology，1995(6):515－537.

［6］ 阚哲，邵富群，丁岚.基于静电传感器的相关流速测量［J］.沈阳工业大学学报，2010，32(1):90－94.

［7］ Gajewski J B.Monitoring Electrostatic Flow Noise for Mass Flow and Mean Velocity Measurement in Pneumatic Transport［J］.Journal of Electrostatics，1996，37:261－276.

［8］ 阚哲，邵富群.基于静电传感器气/固两相流质量流率测量［J］.东北大学学报，2010，31(4):473－476.

［9］ 张瑜，裴东兴，祖静.高压传感器在高静压下的动态校准方法［J］.传感技术学报，2011，24(8):1146－1150.

［10］ 张峰，苑伟政，常洪龙.静电梳齿驱动结构的稳定性分析［J］.传感技术学报，2011，24(8):1126－1130.

［11］ Hammer E A，Green R G.The Spatial Filter Effect of Capacitance Transducer Electrodes［J］.J.Phys.E:Sci.Instrum.，1983，16:438－443.

［12］ Gajewski J B.Electrostatic Inductive Ring Probe Bandwidth［J］.Journal of Electrostatics，1997，6:1766－1775.

［13］ 阚哲，邵富群，李成志，等.插入式静电传感器特性研究［J］.计量学报，2011，32(2):141－146.

［14］ 阚哲.基于静电传感器气固两相流参数测量方法研究［D］.沈阳:东北大学，2010.