不确定数据流自适应并行连接算法及应用*
2012-06-11钱江波王志杰陈华辉王海斌
钱江波,王志杰,陈华辉,王海斌
(1.宁波大学信息科学与工程学院 宁波 315211;2.宁波市公安局 宁波 315040)
1 引言
传统的数据处理中,数据是持久的、确定性的,而查询是短暂、主动的。然而,随着技术的发展,传感器网络、物联网、云计算等许多新的应用领域产生的数据是时变的、不确定的、不可预测的、持续到达的,并且需要在线处理。这种数据驱动的新数据称作不确定或概率数据流,要求系统能够在线、连续、无阻塞地处理。
虽然不确定数据流是无限连续不断的,但是用户一般只关心最近的数据,所以可用滑动窗口进行限定,即无限数据流中时间最近的一个有限子串。执行窗口连接操作时,对于数据流的每个输入元组,都要和其他的数据流滑动窗口中的元组执行连接操作,结果以数据流形式输出。不确定数据流窗口连接是非常重要的操作,具有广泛的用途,如可实时监控套牌车。目前城市中许多摄像设备(如图1中A、B、C)监控行驶中的车辆,每一辆经过的车都会被拍照,并且通过图像识别技术可以获得该车的车牌号。一旦车辆违法,比如超速,根据车牌号等注册信息,车主就会受到罚款。为了躲避处罚系统,一些不法分子将自己的没有牌号的车(如图1中 D)挂上伪造的其他合法车的牌子(如图1中 E)。于是,一旦车D违法,那么根据登记信息,合法车E必将受处罚。文中称D是套牌车。套牌车具有与真牌车相同的车辆型号、相同的车牌号码、相同的车身颜色、相同的行驶证等,整套复制,无法根据车牌及外观特征判断出车辆的真假,因此套牌车的管理难度很大。不确定数据流连接可以解决该难题。所有的摄像设备将车牌、拍摄时间等信息(如图1中F)连续地传到数据中心,形成不确定性数据流。假设在时刻1,车辆D经过卡口A,那么A处的摄像设备将识别出的两个元组(车牌为12345,概率为0.9;车牌为72345,概率为0.1)送到数据中心;在时刻7,E经过C,C将发送两个元组(车牌号12345,概率为0.8;车牌号72345,概率为0.2)。在数据中心,A、C处传出的数据流始终在车牌号属性上执行窗口连接(如图1中 G)。这样,在数据中心将产生具有时间戳之差为6,概率为0.72等属性的连接后的元组。假设从A到C驾车最快需要30 min,D、E若是正常行驶,不可能在30 min之内出现在两地,而现在仅用了 6 min,所以D、E是套牌车的概率是 0.8×0.9=0.72。
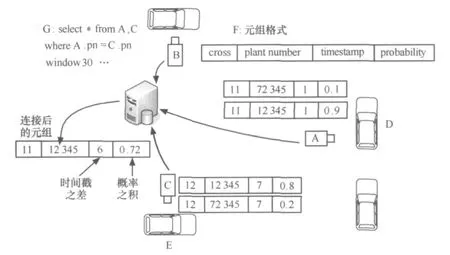
图1 利用窗口连接监控套牌车
这种大量数据流两两并发连接还在传感网应用、网络监控等领域具有广泛用途,而且规模越大,效果越好。但是,大规模的应用也带来大量的计算,影响了处理的速度。因此,不确定数据流并发连接算法非常重要。
2 相关工作
数据流的连接操作需要将一条流中的每一个元组与其他流中的元组做比较。由于阻塞操作并不适用,因此无限数据流上的连接操作一般采用滑动窗口,即两条流之间的连接只需要在当前两个可用窗口之间进行。对称散列连接算法[1]扩展了传统散列连接算法,对于每个数据源A、B,在内存中都维护M个桶。一旦接收到数据源A的新元组 T,如散列值为 Hash(T),则将 T送到 B的 Hash(T)桶进行探测。然后,T被存储到A的Hash(T)桶中。对称连接算法要求两个关系放在内存中,X-join算法[2,3]扩展了该算法,可处理存储在硬盘中的数据。X-join算法在内存中连接,这一点和对称散列连接算法一样。当内存用尽后,将数据源对应的最大的桶写入硬盘。当两个流都阻塞时,X-join算法取出以前存储在硬盘中的数据,然后调入内存进行连接。双管道散列连接算法(DPHJ)[4]是对称散列连接算法的另一种扩展,分两个阶段执行,第一个阶段类似对称散列连接算法和X-join算法,第二个阶段稍有不同。DPHJ适合中等大小的数据块,对较大数据块的操作不太理想。PMJ算法[5,6]是传统排序合并算法的无阻塞版本,主要思想是首先读入内存尽可能多的数据,然后把内存中的数据排序并连接后写入硬盘。当所有数据接收后,PMJ算法允许合并的同时进行连接操作。散列合并算法(HMJ)[7]也是一种无阻塞连接算法,分为两个阶段:散列阶段和合并阶段。散列阶段使用基于散列的内存连接算法,合并阶段主要是当两条流阻塞时进行的,这时算法从硬盘数据调入内存产生连接结果。DINER算法[8]讨论了异构网络环境下,数据流自适应连接的问题,将连接结果多的数据保留在内存中,并能快速切换内存数据连接和磁盘数据连接过程。USJ算法[9]是针对两条不确定数据流连接运算的,通过距离来判断是否能连接,并集成有效剪枝算法增量维护运算结果[10]。针对不同的传感数据,采用不确定模型描述原始数据的不确定性,给出近似的统计方法来获取数据的变化,在时间和空间上都具有很好的效率。
上述文献没有讨论同时多条并发数据流两两连接操作的问题,也没有考虑不确定数据流连接时数据溢出时的操作问题,这些都是本文的讨论目标。
3 定义
此处引入一些概念,这对算法的说明起着很重要的作用。
定义1(不确定性元组)由元组属性和元组存在概率组成。
定义2 (不确定性数据流)不确定性数据流U(t,τ)是无限的、实时的、连续的、有序的元素
定义3 (时间滑动窗口)任意的时刻c,滑动窗口T为数据流上定义的一个子集,该子集包含元组的时间戳为c′,满足 c-c′ 定义4 (连续查询)是常设的、持久的、长期运行的、不间断的查询。在一段时间内,连续查询对数据流不停地、连续地执行查询,对新到来的元组执行操作,增量式产生新的查询结果。 定义5 (连接后的概率)假设有两个不确定性元组, 定义6 (最快行车时间)若从A点到B点之间的道路距离是S,最高限速是v,那么最快行车时间就是S/v。 定义7 (时间矩阵)矩阵的元素time[x][y]的值是地点x与y之间的最快行车时间组成。 本文以套牌车监控为例讨论算法。算法采用由一个分发线程和n个连接线程组成,每个连接线程对应一个探测缓冲区(probe_buffer_i)和一个索引表(ULI)。分发线程从外部缓冲区读入数据,若数据概率小于设定概率阈值,那么连接后元组概率肯定小于阈值,则直接丢弃,否则将元组插入到连接线程的探测缓冲区。 连接线程是最耗时的操作,算法通过散列索引并按概率降序提高查找速度。同时,由于窗口需要删除过期元组,算法采用插入时顺带(实时)删除和批量删除两种方式。时间矩阵用于判断连接后元组是否在同一时间窗口内。i号连接线程处理其他流与i流的连接运算,因此如果是i流元组进入,则需插入,否则需要探测并连接。算法描述如下。 算法1 顺带删除式连接线程i。 图2 连接线程 由于顺带删除窗口内过期元组,相对比较繁琐,也可采用批量删除。批量删除是每间隔固定时间遍历链表,删除过期数据。 不确定数据流窗口连接也可用内存数据库实现。图3是利用内存数据库设计的处理过程,不管规模多大,实现多条不确定数据流窗口连接只需设置两张表 (local和illegal),并通过索引提高速度。 算法描述如下。 算法2 内存数据库处理并发连接。 以上算法是在数据流到来的速度小于或等于CPU的处理速度,内存足够容纳到来数据流的前提下设计的,若数据流速度过高,内存容量偏小时,便会造成数据丢失,部分数据溢出。因此当内存不足时,需从全内存的算法切换到硬盘暂存数据算法,当数据流速度降低时,内存有富余,再将硬盘暂存数据切换回内存。 针对不确定数据流特点,笔者提出当内存用完时,将一部分低概率数据写入硬盘的自适应调整策略。具体策略有两种,期望达到这样一个目的:通过在内存中保留的数据使得得到连接后的数据具有较大的概率,也就是优先输出可能性大的数据。 第一种策略是将窗口数据存储区的部分小概率数据写入硬盘,判断的标准是窗口数据存储区的容量百分比(如将一半写入硬盘,简称窗口一半策略)。如图4所示,假设其他流元组L进入内存探测前,内存已经用尽。采用窗口一半策略,需把median指向的各链表以后的数据都写入硬盘,这时链表中只剩下 A、B、E、F、I,当新数据 L 到来,散列运算到56号索引进行探测连接,假设数据L与F、G满足连接条件,则此时会输出L、F的连接的结果,具有的概率是0.81。而G早写入硬盘无法连接,同时L插入到它自己对应的其他卡口的窗口存储区。等到数据流速度降低时,把写入硬盘的数据G调入内存,这时L与G连接产生的概率为0.765。 图3 内存数据库方案处理过程 图4 窗口一半策略 算法3 将窗口数据存储区一半数据写入硬盘算法。 数据流进入窗口数据存储区中,散列运算到各链表的概率都不同,使连接成功存在不同概率,这个概率称为位置分布概率(prob[i]),其中,具体数值由统计得到。小于概率策略就是尽可能将不会连接成功的小概率元组淘汰,即将存储区中数据具有的概率 (data.prob)与prob[i]之积小于或等于设定写入概率阈值Probability的数据写入硬盘。在图5中,令Probability=0.08,那么当内存用尽时需将链表中对应的小于或等于0.08的数据元素写入硬盘,即将 C、D、E、F、G、H 写入硬盘,A、B、I、J、K 留在内存中继续和新到数据做连接操作。 图5 小于概率策略 由于数据是持续到来的,总是将小于写入概率Probability的数据写入硬盘。一段时间后,留在内存中的数据的概率与位置概率之积越来越接近Probability,写入硬盘的数据越来越少,导致内存的可用空间越来越小。而且部分新数据因小于旧数据(甚至已过期)的概率积,无法驻留在内存进行连接而提前写入硬盘。为避免这种情况,若写入硬盘的数据量小于窗口数据存储区的1/M(win_size/M)时,则将窗口中所有数据都写入硬盘。至于M的取值,应根据内存容量、处理速度以及数据流的速度等历史统计数据决定。 算法4 将小于写入概率阈值Probability的数据写入硬盘算法。 对上述方案进行评估,实验数据分别取真实数据、均匀数据和高斯数据,同时考虑删除时间间隔、概率阈值、线程数量3个主要因素。其中真实数据是某市24 h交通卡口监控数据;均匀数据利用MATLAB 2008a生成,散列运算到索引后使各个链表长度相同,均值为5 000;高斯数据也是MATLAB 2008a生成的,散列运算到索引后能使各个链表长度满足高斯曲线形状,均值为5 000,方差为 50。 实验用多核计算机的配置为 Intel®CoreTM2 Quad CPU Q8400/2.66 GHz/4 GB/250 GB。内存数据库方案的实验环境是 Windows XP Professional、Timesten 11内存数据库、VC6.0;多线程方案的环境是 Fedora 13、GCC编译。 设概率阈值为0.7,时间矩阵的元素为60 min,各个处理线程对应的探测缓冲区为300 KB,每个线程的索引表为10 000个索引号,删除时间间隔为60 min。分别使用均匀、高斯、真实3种数据,一个分发线程,讨论分别采用30、60、90、120、150 个处理线程时情况。 从图6~8可以看出,无论是多线程实时数据处理方案还是多线程批量数据处理方案,总的趋势都是随着卡口数量(卡口数量等于处理线程数量)的增多,数据的处理速度降低。这主要是由于线程的运行受硬件配置的影响,在某一段时间内,卡口数量少时,处理线程的数量也必然少,各个线程运行的次数相对较多,而卡口数量增加时,处理线程增加,在同样的时间段内,每个线程获得的运行次数就相对减少,但每个线程处理的数据量又不会减少,故导致单位时间内处理的数据量减少,即速度减小。对于Timesten内存数据库来说,由算法2可知与卡口数量无关,故保持恒定的速度。从图6~8可以看出,在150个卡口以内,多线程方案的处理速度是内存数据库方案速度的2~8倍。 图6 均匀数据下卡口数量变化对数据处理速度的影响 图7 高斯数据下卡口数量变化对数据处理速度的影响 图8 真实数据下卡口数量变化对数据处理速度的影响 设概率阈值为0.7,时间矩阵的元素为60 min,各个处理线程对应的探测缓冲区为300 KB,每个线程的索引表为10 000个索引号。分别使用均匀、高斯、真实3种数据,一个分发线程,60个处理线程,讨论删除时间间隔分别采用 30、60、90、120、150 min 的情况。 图9 均匀数据下删除时间间隔变化对数据处理速度的影响 图10 高斯数据下删除时间间隔变化对数据处理速度的影响 图11 真实数据下删除时间间隔变化对数据处理速度的影响 从图9~11可以看出,多线程方案的处理速度都是先增大后减小,其中对真实数据和高斯数据而言,它们在删除间隔等于60 min左右时出现速度最高点,对均匀数据而言在删除间隔等于90 min左右时出现速度最高点。多线程批量数据处理方案和内存数据库方案进行过期清理都是扫描全部数据,删除间隔较小时,造成了程序运行过程中频繁扫描所有数据,增大了系统的开销。随着删除间隔的增大,这种系统开销会相对降低,速度逐渐提高。但是当删除间隔变得很大时,从缓冲区读出的新数据需要和本地链表或存储表中大量积累的数据做比较,这样无效比较次数必然增多,故速度又会降低。所以总的速度趋势就是先增大后减小。但是删除时间间隔对内存数据库影响明显小于多线程批量数据处理方案。对于实时数据处理方案而言,它本身就是在插入和探测比较操作前,先判断插入或比较位置处的数据是否过期,即时进行过期清理,故和实验中设置的删除间隔大小没有必然关系,所以大小一直恒定不变。从这3幅图可以看出两种多线程方案明显优于内存数据库方案,并且多线程实时数据处理方案要略胜于批量数据处理方案。 设时间矩阵的元素为60 min,各个处理线程对应的探测缓冲区为300 KB,每个线程的索引表为10 000个索引号,删除时间间隔为60 min。分别使用均匀、高斯、真实3种数据,一个分发线程,60个处理线程,讨论概率阈值分别采用 0.7、0.8、0.9 时的情况。 从图12~14可以看出,3种方案的数据处理速度都是随着概率阈值的增大而升高,这是由于概率阈值越大,程序运行过程中丢弃的数据就越多,实际需要进一步深入处理的数据量减少,于是单位时间内数据处理读入数据的数据量增大,即处理速度提高。两种多线程方案的处理速度随着概率阈值的增大,处理速度的增幅要比内存数据库方案的增幅要大,并且多线程实时数据处理方案比批量数据处理方案速度稍高,多线程数据处理方案比内存数据库处理速度要高。 图12 均匀数据下概率变化对数据处理速度的影响 图13 高斯数据下概率变化对数据处理速度的影响 图14 真实数据下概率变化对数据处理速度的影响 从上述3种实验的9幅图可以看出,3种数据对内存数据库方案的速度基本没有什么影响,这是由于内存数据库将所有的数据都存储在一个本地存储表中,凡是从缓冲区读入的新数据,经过过滤后,都要按车牌号形成的索引搜索整个表格,数据的种类已经不会对其产生太大影响。对两种多线程策略而言,均匀数据的处理速度最快,高斯数据的处理速度最慢。这是由于多线程的数据处理方式是当数据到来时,首先要根据对应的索引号去确定特定的链表,当确定了链表后,所有的操作仅在该链表中进行,对于均匀数据而言,它形成的所有链表的长度基本相同,而高斯数据形成的链表长度不一,其中间部分偏长,两端较短,这样,均匀数据在链表中进行数据处理扫描的链表平均长度,就明显比高斯数据到来时处理的平均链表长度要短,所以说均匀数据的处理速度高,高斯的要低。正是因为这个原因,在第二种实验中均匀数据要到达速度最高点的时刻要稍晚于高斯数据。真实数据介于均匀数据和高斯数据之间,所以处理速度也介于两者之间。 为了能够使实验结果更加明显,本部分的评估仅使用均匀数据作为实验数据,车牌号均匀数据是利用MATLAB 2008a生成的、散列运算到索引后能使各个链表长度相同的数据,均值为1 500,范围是1 000~1 999,概率数据均匀分布在0.5~0.99。时间矩阵的元素为60 min,探测缓冲区为1 500,每个线程的索引表为1 000个索引号。概率阈值设为0.7。对于算法3,窗口存储区满后将一半写入硬盘;对于算法4,因为车牌数据是均匀的,每个数据散列运算到各个链表的概率相同,所以简化位置概率prob[i]=1,写入概率阈值Probability=prob[i]×data→prob=data→prob=0.8,N=M=3。 图15 不同方法在不同时间段输出结果平均概率分布 图16 不同方法在不同时间段输出结果数据分量分布 从图15、16可以看出,数据全在内存的方法最快,因为内存充足,所有的操作数据均在内存,不需要任何的硬盘I/O操作,节省了大量时间。对于窗口一半算法,内存用尽时,一半具有较低概率的数据写入硬盘,留在内存的都是具有较大概率的数据,通过与它们进行连接操作得出的数据具有的概率要偏高,图15中显示与内存中驻留的数据发生连接操作得出的结果具有较大概率,通过以后调入硬盘中的数据得出的结果具有较小概率。对于小于概率算法,也得到类似的结果。但是两者相比,窗口一半算法中留在内存数据执行连接操作用的时间偏短,这是由于概率均匀分布在0.5~0.99,而0.5~0.7的数据已被分发线程丢弃,这样进入内存的数据的概率就分布在0.7~0.99,Probability=0.8,也就是说,窗口一半算法留在内存的数据的概率最小在0.85左右,小于概率算法留在内存的数据具有的最小概率稍大于0.8,这样其新数据到达内存连接时,和窗口一半算法留在内存中的数据比较的次数要少,所以用时偏少,同时得出的违法结果也少。当然,无论是内存方法还是硬盘策略,得出的违法结果是相同的,只是发现的时间不同,这样窗口一半算法在硬盘得出的数据就比小于概率方法得出的偏多,这分别在图15、16中可以看出。由于硬盘两种策略写入硬盘的数据量大致相同,所以它们总时间基本相同,而小于概率算法提前得出的数据值偏多,所以推荐使用此方法。 针对大规模不确定数据流的并发连接,本文提出了一系列高速在线处理的算法。主要贡献有: ·提出监控套牌车的方法,解决目前无法发现套牌车的难题; ·设计实现大规模并发连接的算法,为大规模监控套牌车提供基础; ·提出不确定数据流连接操作时,内存溢出情况下的数据调度策略,确保概率高的运算结果及时输出; ·使用真实数据、均匀数据、高斯数据进行实验评估,证明算法具有良好的性能,其处理速度比内存数据库Timesten速度提高2~8倍。 1 Wilschut A N,Apers P M G.Dataflow query execution in a parallel main-memoryenvironment.ProceedingsoftheFirst International Conference on Parallel and Distributed Information Systems,PDIS,Miami,Florida,1991 2 Urhan T,Franklin M J.XJoin:Getting Fast Answers From Slow and Burst Networks. Technical Report CS-TR-3994,UMIACS-TR-99-13,Computer Science Department,University of Maryland,1999 3 Urhan T and Franklin M J.XJoin:a reactively-scheduled pipelined join operator.IEEE Data Engineering Bulletin,2000,23(2):27~33 4 Ives Z G,Florescu D,Friedman M,et al.An adaptive query execution system for data integration.Proceedings of the ACM International Conference on Management of Data,SIGMOD,Philadelphia,PA,1999 5 Dittrich J P,Seeger B,Taylor D S,et al.Progressive merge Join:a generic and non-blocking sort-based Join algorithm.Proceedings of the International Conference on Very Large Data Bases,VLDB,Hong Kong,2002 6 Dittrich J P,Seeger B,Taylor D S,et al.On producing join results early.Proceedings of the ACM Symposium on Principles of Database Systems,PODS,San Diego,CA,2003 7 Mohamed F Mokbel,Ming Lu,Walid G Aref.Hash-merge Join:a non-blocking Join algorithm for producing fast and early Join results.Proceedings of the 20th International Conference on Data Engineering,Boston,MA,USA,2004 8 Mihaela A Bornea,Vasilis Vassalos,Yannis Kotidis,et al.Adaptive Join operators for result rate optimization on streaming inputs.IEEE Transactions on Knowledge and Data Engineering,2010,22(8):1 110~1 125 9 Xiang Lian,Lei Chen.Similarity Join processing on uncertain data streams.IEEE Transactionson Knowledge and Data Engineering,2010,22(10):1 312~1 319 10 Diao Y,Li B,Liu A,et al.Capturing data uncertainty in high-volume stream processing.Proc Conf on Innovative Data Systems Research,Asilomar,CA,USA,20094 内存充足情况下的连接算法
4.1 内存充足时多线程连接算法

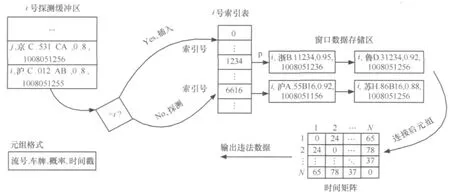

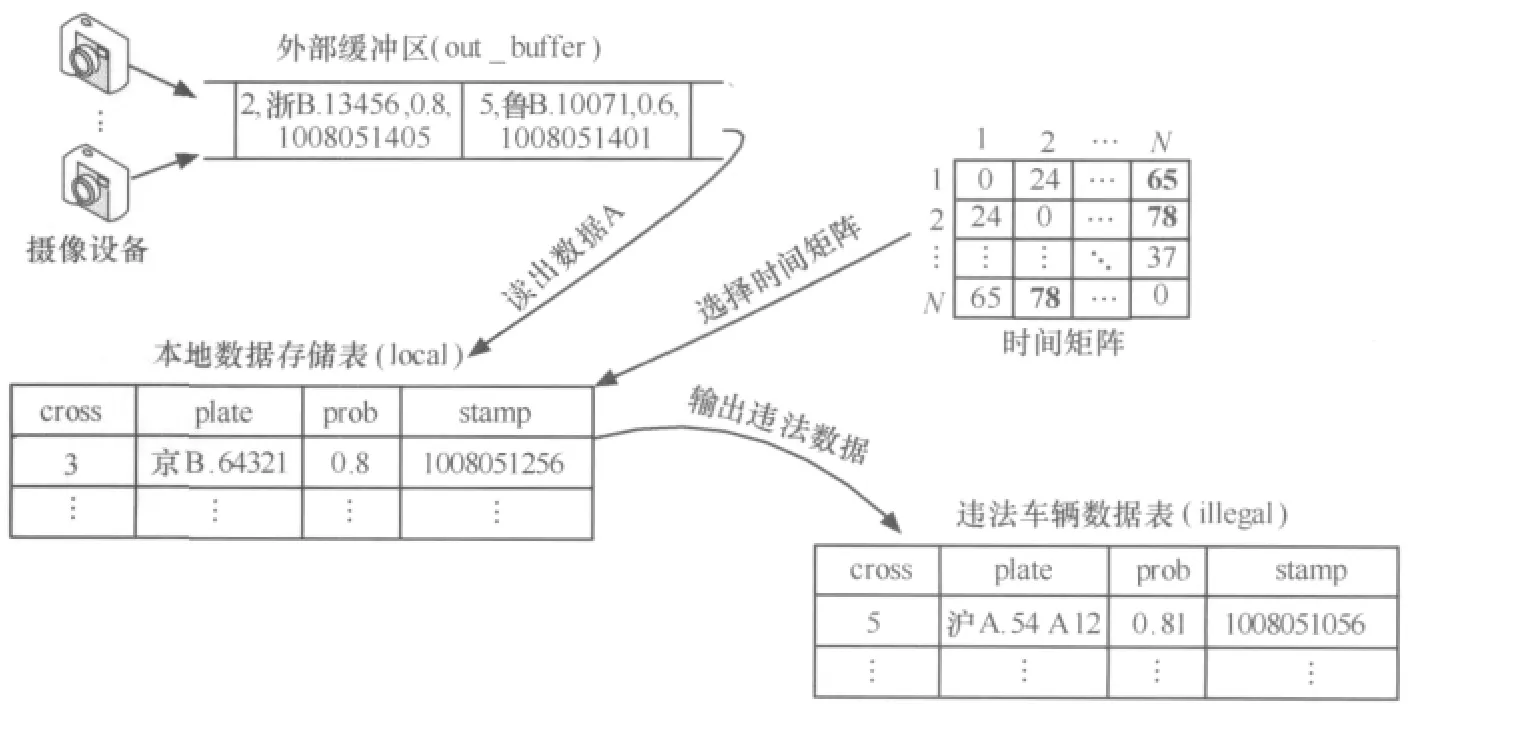
4.2 内存数据库算法


5 内存溢出时替换算法
5.1 窗口一半策略
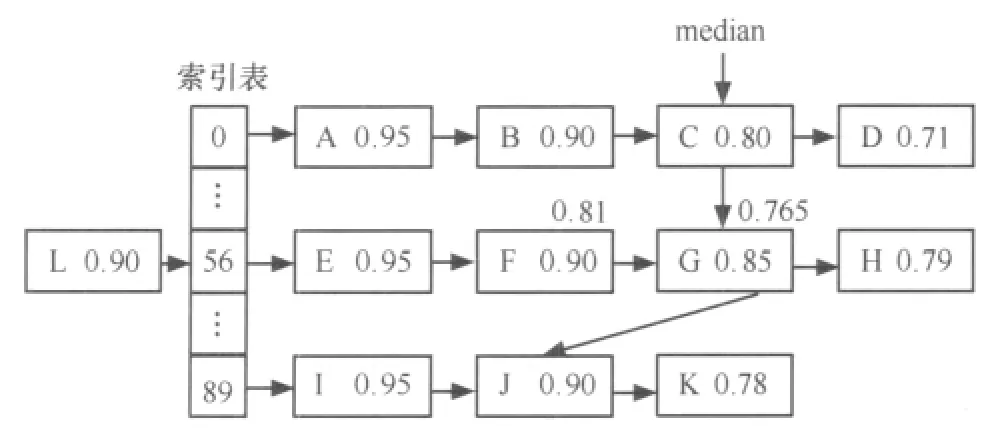

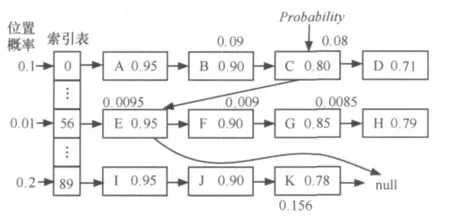
5.2 小于概率策略


6 实验结果
6.1 线程数量的变化对数据处理速度的影响
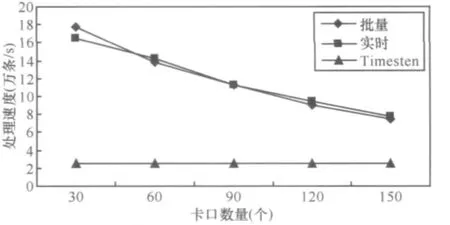
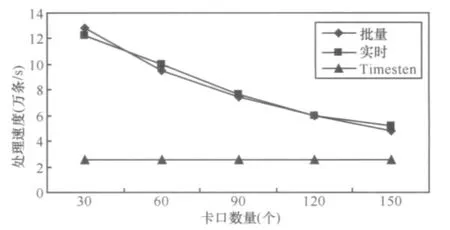
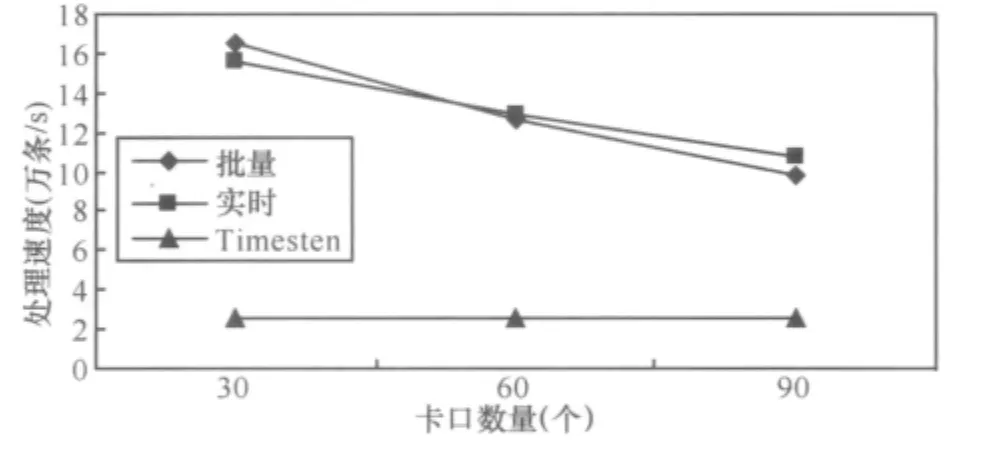
6.2 删除时间间隔对数据处理速度的影响
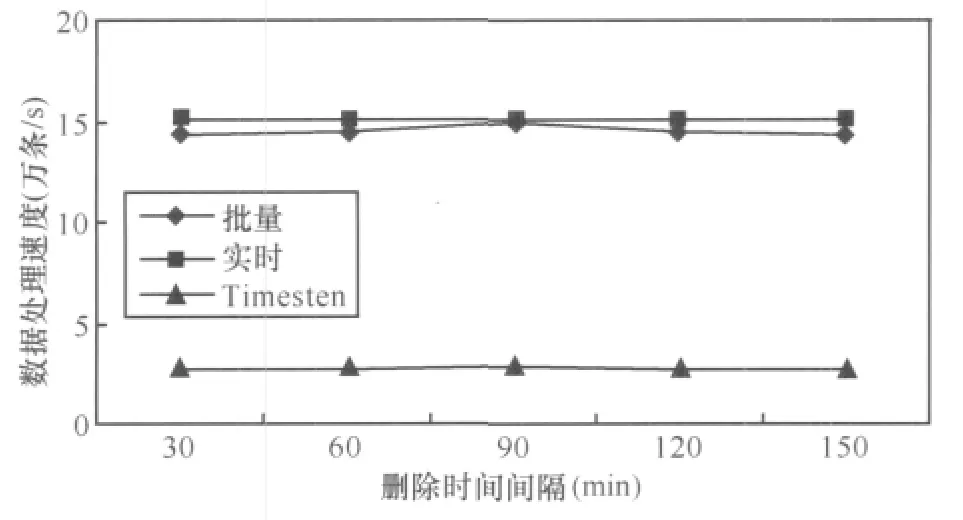
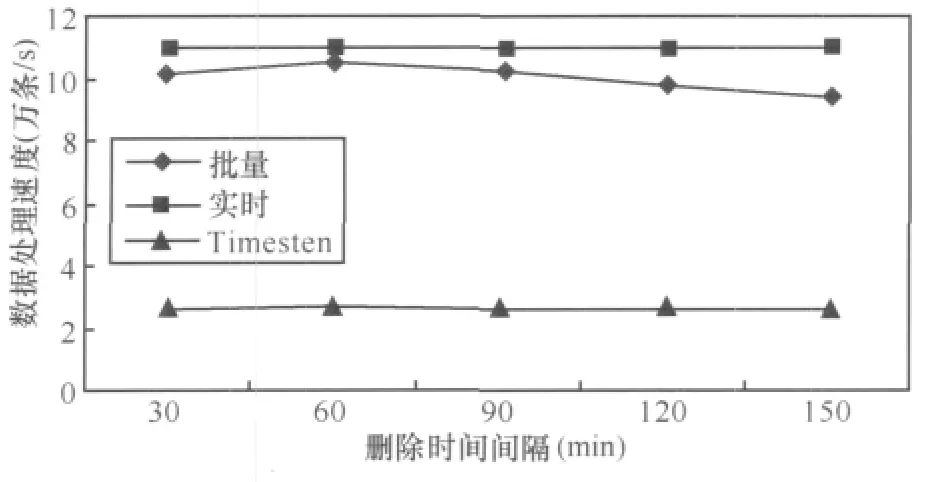
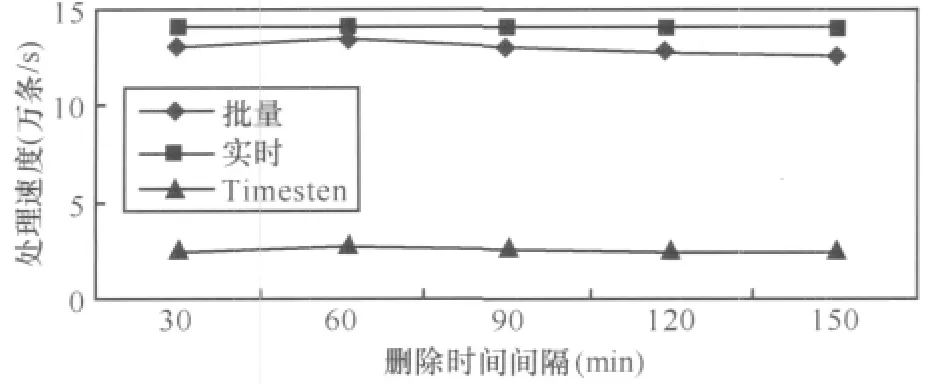
6.3 概率阈值的变化对数据处理速度的影响
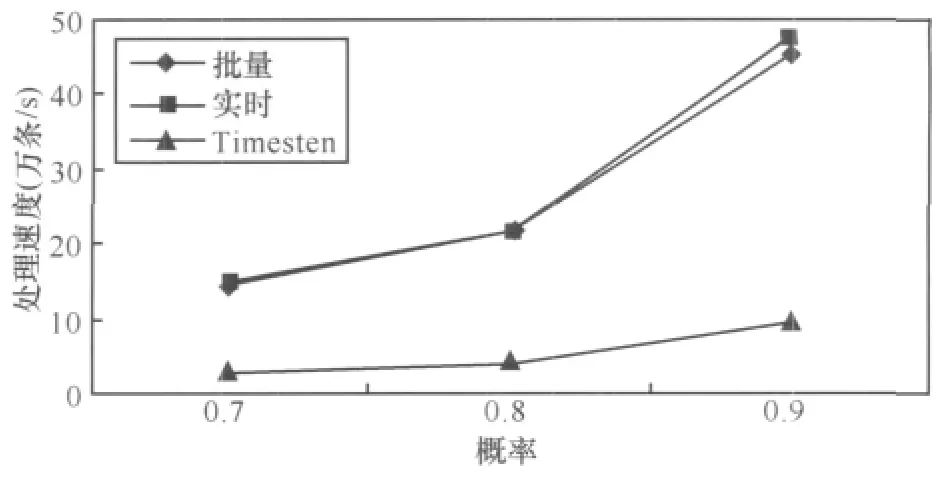
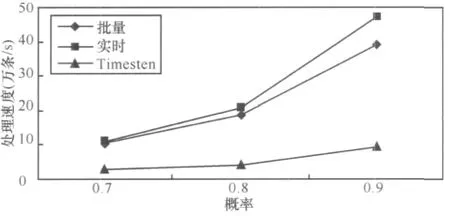
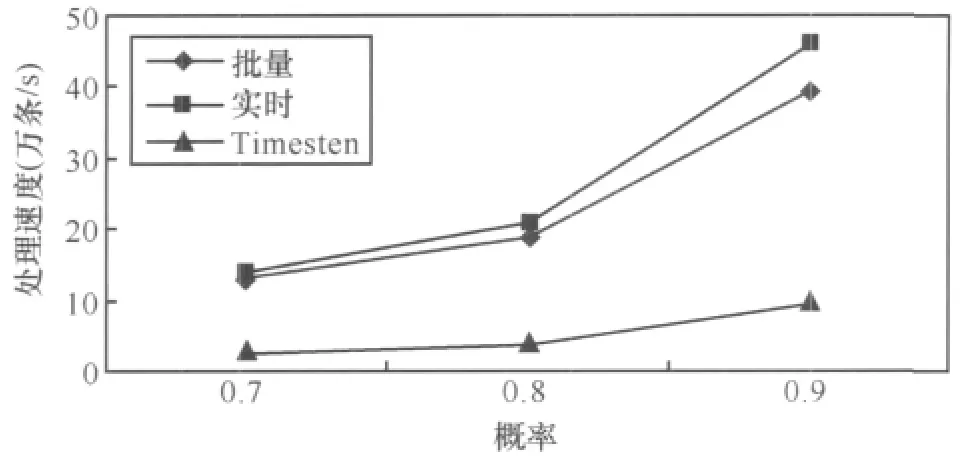
6.4 全在内存策略与两种部分写入硬盘策略对比实验
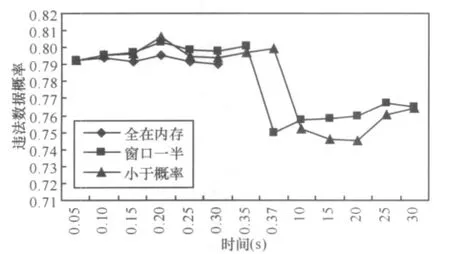
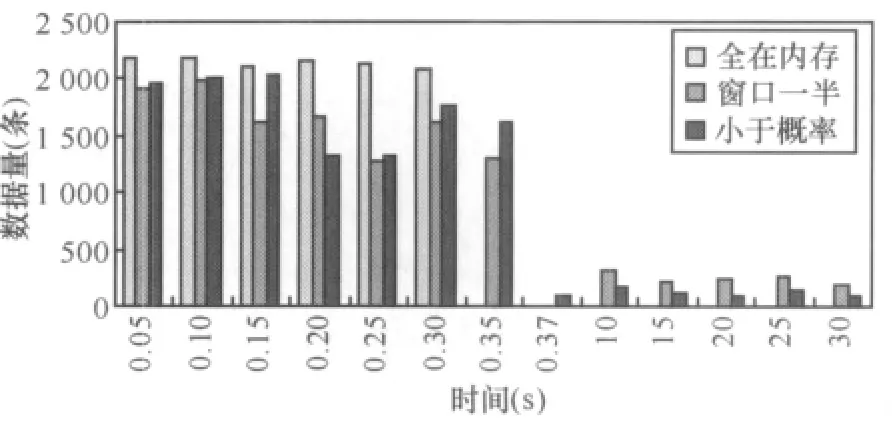
7 结束语
