一种改进的基于Hadamard 域的码书设计算法*

王佳果，陈善学，张 艳，尹雪娇

(重庆邮电大学移动通信安全技术实验室 重庆400065)

1 引言

矢量量化（vector quantization,VQ）[1,2]是一种高效的有损数据压缩技术，因其具有压缩比高、编解码速度快的特点，被广泛地应用于话音编码和图像的压缩系统中。码书设计[3]是矢量量化研究的一个关键技术，研究码书设计算法的根本目的是寻求一种有效的算法来尽可能地找到全局最优或者接近全局最优的码书以提高码书的性能，码书设计的好坏关系到整个矢量量化器设计的成功与否，是决定矢量量化器性能的主要因素。

矢量量化的基本思想[4]是：把图像看成是一串数据，设这一串数据大小为m，把它截成M段(一般每段相等，例如为k)，即把m个数据变成了M个矢量，再把这M个矢量分成N组，对每个组挑选一个数据矢量作为这个组的代表，例如第 j个组的代表为 yj(j=0,1,…,N-1)。集合{yj|j＝0,1,…,N-1}称为码书。其中N称为码书长度或码书大小。一个k维、尺寸为N的矢量量化器可以定义为从k维欧几里德空间Rk到其一个有限子集C的一个映射，即Q:Rk→C,C={y1,y2,y3,…,yN}。通常将集合C称为码书，N为码书长度。该映射满足：Q(x|x∈Rk)=yp，其中 x=(x0,x1,…,xk-1),yp=(yp0,yp1,…,yp(k-1))，并且满足：

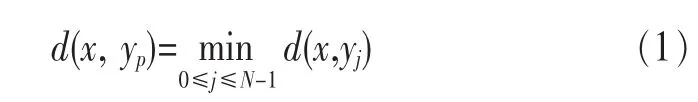
其中d(x,yp)为矢量x与码字yj的失真测度，通常采用的失真测度是欧式距离的平方，其表达式为：

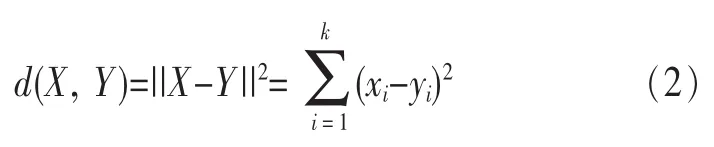
LBG算法[4]是关于码书设计的经典算法，其为矢量量化技术的发展奠定了基础。LBG算法主要依据两个准则：一是最佳划分准则，即对于给定码书，训练矢量集的最佳划分可通过把每个训练矢量映射为离它最近的码字得到。二是最佳码书准则，即对于给定训练矢量划分，最佳码书的各码字为各胞腔的质心。传统的码书设计算法LBG算法，主要存在3个缺点[5]:对初始码书非常敏感；码书自适应能力不强；运算量大，这些缺点也就限制了LBG算法的应用。LBG算法的步骤如下[6]。

（1）初始化码书。即采用训练矢量随机抽取法选定初始码书YN(0)={Yj|j=1,…,N}，设置迭代次数n=0，平均失真D-1→∞，给定相关门限 ε(0<ε<1)。

（2）聚类过程。根据最近邻原则，把训练集X={xm|m=1,2,…,M}中的矢量xm划入到N个不同的子区间Si(n)(i=1,2,…,N)中，其中，Si={xj:d(xj,yi)=min d(xj,yl)}，对于任意 l∈i{1,2,…,N}成立。

LBG算法初始码书中采用的训练矢量集是随机抽取法，即将M个训练矢量平分成N组，在每组中选取一个训练矢量作为初始码字。参考文献[7]是Chen的一种LBG改进算法，Chen的算法主要是引进范数，对训练矢量采用按矢量和值进行排序生成码书。

但Chen的算法也存在着初始码书随机性较强和搜索获胜码字计算量较大的缺点。为此改进算法使用了新的初始码书生成方法使得编码性能得到了改善，同时还引入了一种搜索获胜码字的快速算法降低了搜索码字过程中的计算量，并且获得的初始码书首先经过Hadamard变化，使算法简单，计算量小。

2 改进算法

2.1 Hadamard变换的定义和性质

令Hn为 2n×2n的 Hadamard[8,9]矩阵，其元素属于集合{-1,1}，假定以下所有矢量为k维矢量，k=2n(n>0)，则可得到以下基本定义和性质。

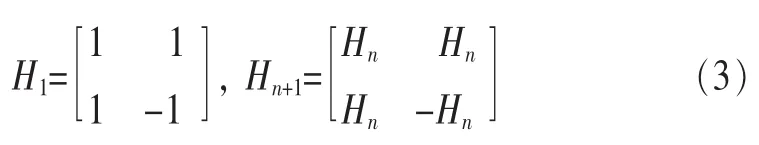
矢量x的Hadamard变换矢量X可定义为：

X1=Sx，这里X1是矢量X的第一维分量，Sx为空域中输入矢量x的和值。

D(X,Yj)=kd(x,yj)，Yj为码字 yj的 Hadamard 变换。

由此可以看出Hadamard变换前后的能量成倍数关系，在Hadamard域和空域中搜索最近邻码字是等价的。

2.2 算法步骤

在 k 维适量空间中[10]，训练矢量 X=（x1,x2,…,xk）和初始码书Y=(Yj,j=1,…,N)，码书大小为N。矢量X和Y的矢量和、方差和二范数分别为（Sx,Vx,Lx）和(Sj,Vj,Lj)，则：

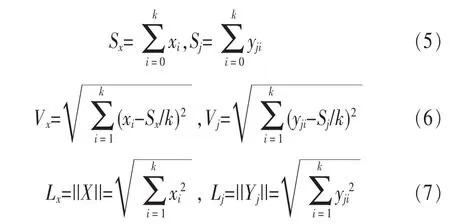
H(k)为 k×k维 Hadamard矩阵，矢量 X和码书 Yj经Hadamard变换为 hx和hyj，并且有 hx=XH(k)和hyj=YjH(k)，则hx和hyj的方差和二范数为：

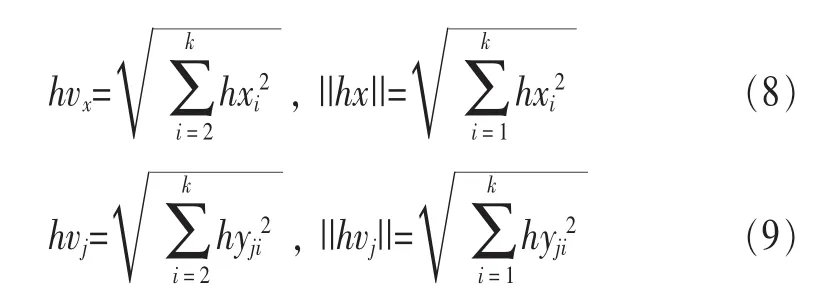
本算法首先对训练矢量进行Hadamard变化，计算其范数，并按照范数大小进行排序，然后按照码书大小进行平均分组，选择每组第一个训练矢量作为初始码书。假设当前最小失真为Dmin，hx1和hyj1分别是hx和hyj第一维分量，则有以下3步排除准则。

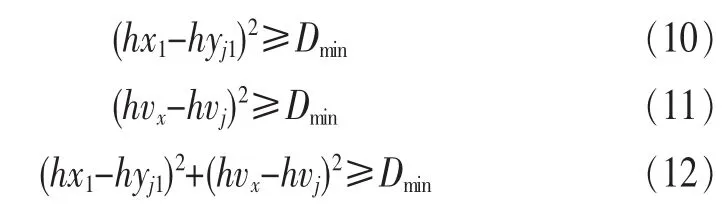
在N个码字中寻找与Dmin相等的码字，即当前获胜码字Yp，此时将训练矢量X划分到第P个胞腔，计算其质心替代当前获胜码字Yp，输入下一个训练矢量，直到所有训练矢量被训练完为止，此时令迭代次数t→t+1，直到达到所要的迭代次数。本算法结合LBG算法优点，利用统计特征量的分类平均法生成初始码书，同时引入快速搜索算法，克服LBG算法的两个缺点，而在每个训练矢量找到匹配码字后，利用求质心的方法调整码字，更能够匹配整个胞腔，而且加速了码书的收敛速度，提升了码书的性能。

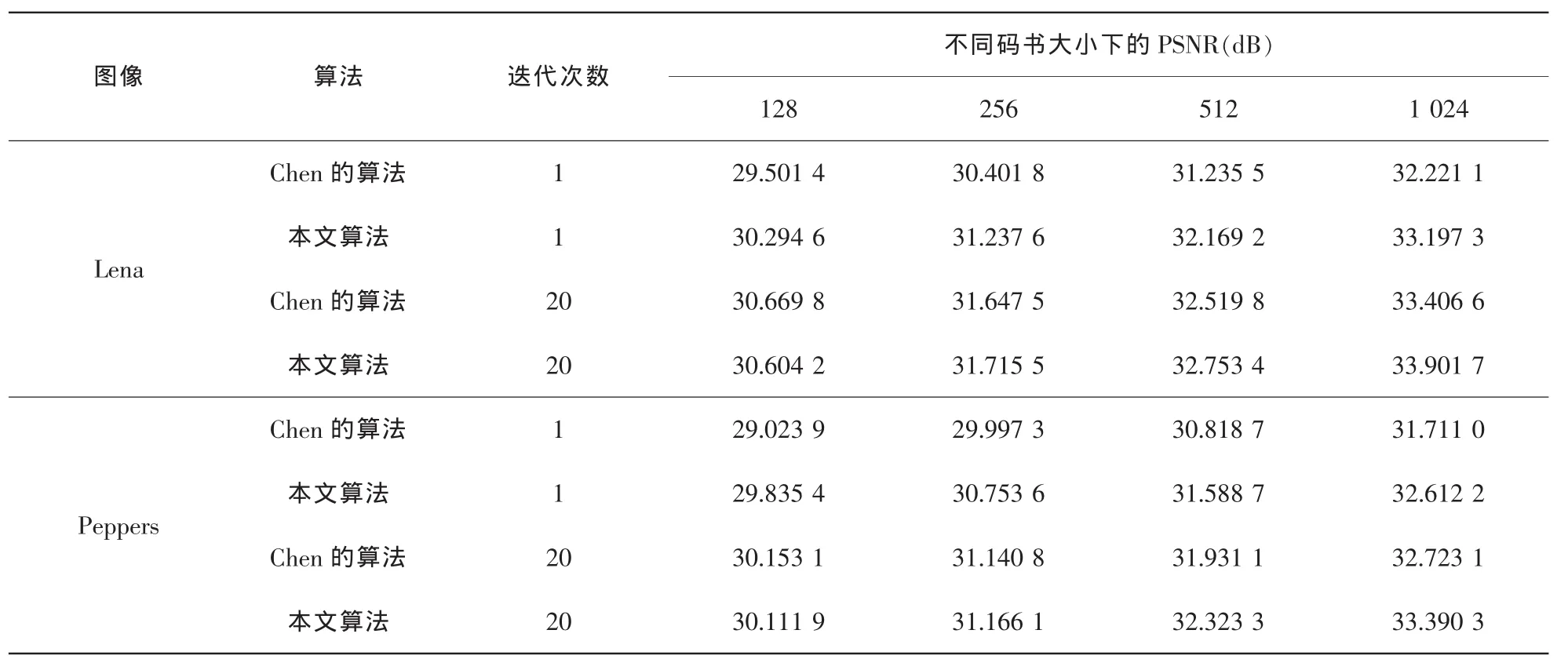
表1 改进算法的编码效果（PSNR）比较

表2 计算复杂度的比较

3 实验仿真结果

仿真实验采用 512×512×8 bit的灰度 Lena图像和Peppers图像作为测试图像，经Hadamard变换后按第一维升序排列生成初始码书，码书大小分别为128、256、512、1 024。首先比较改进算法和参考文献[7]的算法在迭代次数为1和20的情况，如表1所示，因为算法的运算时间与电脑性能以及编程技术有关，所以本算法不进行运算时间的比较，而是只比较算法压缩后图像的恢复效果和计算复杂度。表1比较了改进算法和Chen算法的峰值信噪比（PSNR）；图1比较了改进算法和Chen算法在不同迭代次数下的峰值信噪比，其中码书大小为512；表2比较了改进算法和Chen算法的计算复杂度。

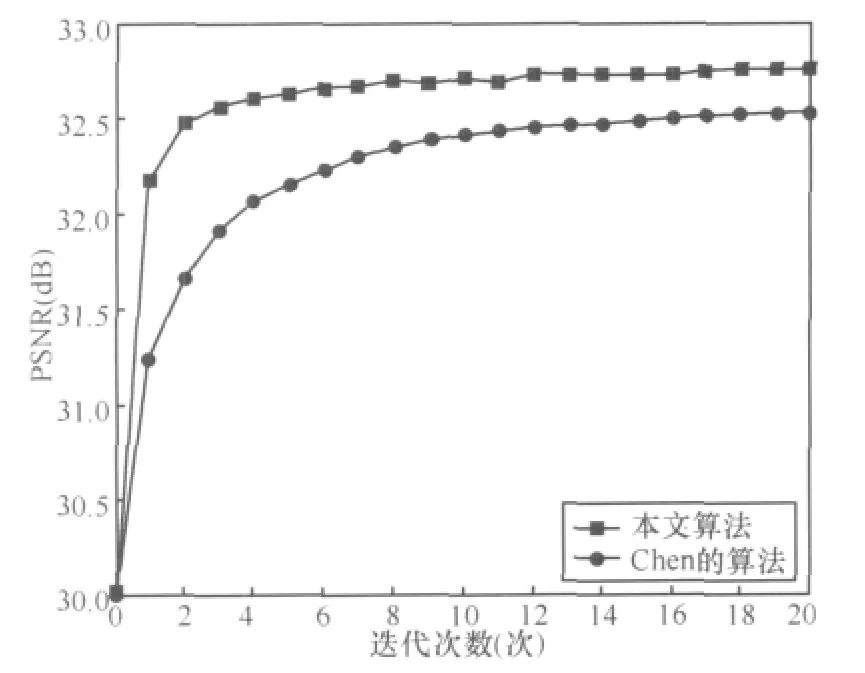
图1 两种算法在不同迭代次数下的峰值信噪比（PSNR）

从表1可以看出，本算法相比Chen的算法有很大的提高，尤其在迭代次数较小的情况下，算法的提升非常明显，PSNR的提升最大达到0.9 dB。图1表示的是两种算法在码书大小为512的情况下，不同迭代次数下的PSNR，可以看到，本算法在较低迭代次数就能达到较好的效果，并且快速达到稳定，说明本算法码字排查效率很高。从表2可以看出，本改进算法在计算复杂度上并没有明显增加，从而说明本算法在没有增加计算复杂度的情况下，对图像的恢复效果，即PSNR，有较好的提高。

4 结束语

本文结合Hadamard变换和K-means理论，在对Chen的算法研究基础上，针对初始随机性强和排除码字效率不高的特点进行以下改进：对初始码书按Hadamard变换后计算其二范数，并按其范数大小进行升序排列，按码书大小进行选取，利用统计特征量的分类平均法生成初始码书，然后提高求质心的频率，每当一个训练矢量被分类到胞腔时，就求出相应胞腔的质心来代替原有的码字。从实验数据上可以看出，在迭代次数较小时改进算法的PSNR相比Chen的算法提高了0.5～0.9 dB，在迭代次数较小时说明改进后的初始码书更能代表输入矢量的数据分布情况，更易快速收敛。而在迭代次数较大时，本算法也较Chen的算法有0.2～0.3 dB的提高，体现了本算法的优势。相比Chen的算法，调整后的码字代表了整个胞腔的特性，更能够匹配整个胞腔。引入3步快速排除准则，可以较高效率排除不必要的码字，加速了码书的收敛速度，提升了码书的性能。

1 Nasrabadi N M，King R A．Image coding using vector quantization：a review．IEEE Trans Commun,l988，36(8)：957～971

2 Linde Y,Buzo A,Gray R M.An algorithm for vector quantizer design.IEEE Trans Commun,1980,28(1):84～95

3 陈善学，李方伟.矢量量化与图像处理.北京：科学出版社，2009

4 孙圣和，陆哲明.矢量量化技术及应用.北京：科学出版社，2002

5 Rui Xiayi,Yu Yibiao.A new codebook design method based on genetic algorithm for text-independent speaker identification.Signal Processing,2005,21(3):289～292

6 刘丽娟，邹雪城，沈绪榜.一种新的矢量量化编码算法.小型微型计算机系统,2004,25(10)

7 Chen Shanxue,Li Fangwei,Zhu Weile,et al.Initial codebook algorithm of vector quantization.IEICE Trans Inf&Syst 2008,E91-D(8):2 189～2 191

8 Lu Z M,Chu S C,Huang K C.Equal-average equal-variance equal-norm nearest neighbor codeword search algorithm based on ordered hadamard transform.International Journal of Innovative Computing,Information and Control,2005,1(1):35～41

9 Chu S C,Lu Z M,Pan J S.Hadamard transform based fast codeword search algorithm for high-dimensional VQ encoding.Information Sciences,2007,177(3):734～746

10 Lai J Z C,Liaw Y C.Fast-searching algorithm for vector quantization using projection and triangular inequality.IEEE Trans Image Process,2004,13(12):1 554～1 558