2 000 t压力机横梁结构强度及动态特性分析

任志江

(新筑公司 搅拌机械研究所，成都 611430)

在机械制造中，压力机广泛应用于切断、冲孔、落料、弯曲、铆合和成形等工艺。目前压力机的结构设计仍然是采用传统设计方法:即利用材料力学简化计算与经验设计相结合的方法。虽然实践证明具有一定的可靠性，但仍然存在许多弊端:如设计周期长，机构组件冗余，结构笨重且用材量大，成本高，效益低［1～2］。压力机横梁是压力机的重要组成部件，在冲击作用下，其强度和刚度是设计所关注的重点。有限元法在结构中的应用为大型复杂结构件的结构分析提供了一种高效、精确的分析方法［3］。本文采用有限元法以某企业开发的公称压力为2 000 t压力机横梁为研究对象，对该型压力机横梁进行结构强度计算和模态分析，为车架改进优化提供理论依据及基础数据。

1 压力机横梁有限元模型

1．1 横梁CAD模型及技术参数

该型压力机横梁由3部分构成:中间横梁及与中间横梁两端相配的上支座，采用焊接连接，如图1所示。横梁通过上支座与压力机立柱螺栓连接。在建立横梁总成模型时，采用国标统一标准单位。

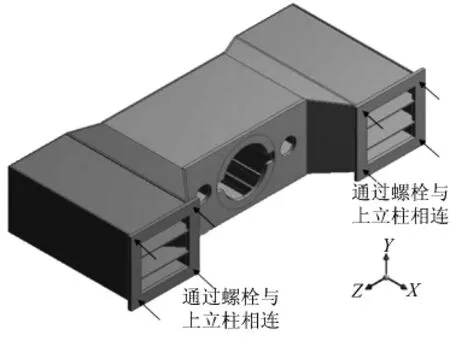
图1 压力横梁几何模型

从图1中可以看出，该型压力机横梁总成为钢板焊接而成的箱型结构，结构上完全对称，其总长(Z方向)为9．02 m，总宽(Y方向)为2．01 m，总高(X方向)为3．928 m。材料均采用CCSDH32高强度船板用钢，材料密度为7．88×103kg/m3，抗拉强度为440～570 MPa，杨氏模量为2．1×1 011 Pa，泊松比为0．29［4］;中间横梁总质量为 23．92 t，单个上支座质量 18．34 t，整个横梁总成总质量为 60．6 t。

1．2 单元选择及模型离散

本文借助ANSYS Workbench12．1分析计算，考虑求解精度、计算时间和对计算机硬件要求，选择软件默认的Solid186单元离散该横梁。通过软件离散后，得到横梁的有限元模型(如图2)。离散后，整个横梁总成一共60 344个单元，节点数为112 286。

2 横梁结构强度和刚度计算

约束处理:横梁总成两端上支座与下立柱螺栓连接，在作用力下，下立柱仅处于受拉状态，在实际工作中，压力机下立柱拉伸变形很小，且其强度和刚度与横梁总成相互独立，所以在此假定下立柱为刚体，直接在横梁总成的上支座与下立柱相连处施加全约束。

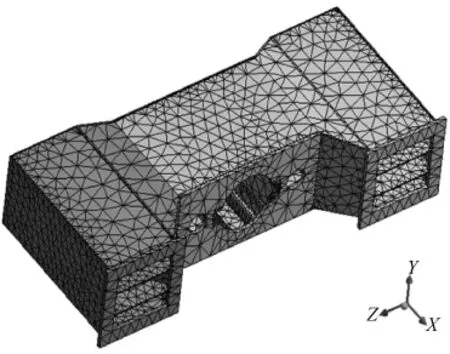
图2 横梁有限元模型

载荷处理:由于该型压力机设计的最大工作载荷为2 000 t，通过液压缸作用于横梁上，在有限元模型中，通过选取与液压缸相配位置并将载荷施加于相应位置;车架自重通过惯性力施加，取重力加速度为9．8 m/s2。

通过ANSYS Workbench12．1软件计算，得出横梁总成的应力分布情况如图3所示，其最大应力为342．6 MPa，位于图3中所示A点，此处为横梁与液压缸相配处内部的加强板;由于模型、载荷及边界条件均保持对称，所以整个横梁应力分布在长度和宽度方向保持对称;从图3中可以看出，整个横梁高应力区较少，大部分处于72 MPa以下，特别是两端上支座，其应力均处在36 MPa以下;同时也可看出该横梁总成还可以进一步优化。

横梁总成的位移变形如图4所示，最大位移为2．5 mm，位于中间横梁与液压缸相配处。同样，模型位移变形也保持对称。整个横梁变形分布由中间到两边逐渐变小，这也符合实际工作工况:中间受载最大且离约束最远。

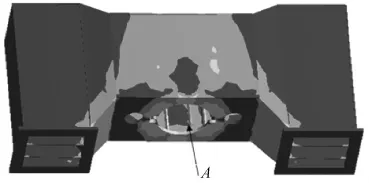
图3 压力机横梁压力场分布

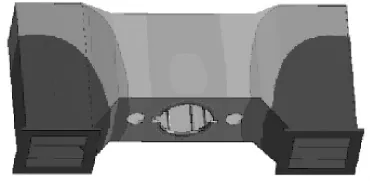
图4 压力机横梁位移分布

3 横梁总成模态分析

机械结构的动态特性用结构的振动模态参数来表示，即结构的各阶频率，阻尼及振型［5］。而系统的固有频率及振型是系统的固有属性，不受其他因素影响。因此通过这些模态分析的结果就可以判定横梁结构动态特性。

3．1 理论基础

根据达朗贝尔(D’Alembert)原理，在结构承受的载荷中加入惯性力，建立动力学方程:

其中:M为结构总质量矩阵;C为结构的阻尼矩阵;δ为节点位移列阵;K为结构总刚度矩阵;Fp为节点等效载荷列阵。

在求结构的固有频率和振型时可不考虑阻尼的影响，在结构的动力学方程中:令C=0，同时令Fp=0，得到无阻尼自由振动方程为:

弹性自由振动的振型可分解为一系列的简谐振动的叠加，将其解设为:

将(3)式代入(2)中可得下面的齐次方程组:

在自由振动时，结构中各点的振幅δ0不全为零，所以(4)式中括号内矩阵的行列式必为零，得到结构的自由振动频率方程为:

矩阵K和M都是n阶方阵，其中n是结点自由度数目，所以，式(5)是关于ω2的n次实系数方程，从中解出n个实根 ωi2时(i=1，2，3，…，n)，即特征值，按由小到大的顺序排列ω12≤ω22≤…≤ωn2，把任一ωi2代回方程组(4)可解出与其相对应的矢量δi(i=1，2，3，…，n)。ω ，01ω2，…，ωn就是结构的第1阶，第2阶，到第n阶的固有频率，与其对应的δ01，δ02，…，δ0n则是第1阶，第2阶，…，第n阶的主振型［6］。

图5 压力机横梁第1阶模态振型

3．2 分析结果

低阶固有频率及相应的振型对动态特性的影响较大，限于篇幅，本文提取横梁总成的前10阶固有频率和振型，并列出前4阶振型如图5，6，7，8所示。前10阶模态频率如表1所示。

图6 压力机横梁第2阶模态振型

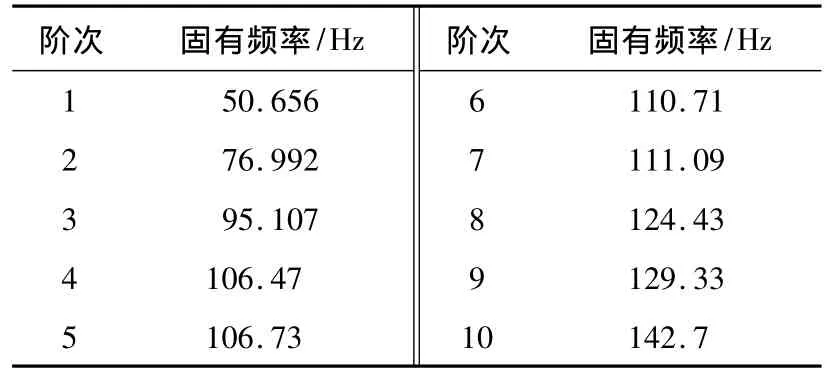
表1 横梁总成前10阶固有频率

通过前4阶振型图可知，横梁前4阶最大振幅均发生在横梁顶部，第1阶为横梁中间，第2阶和第3阶为横梁上支座左右两侧上支座，第4阶为左右2支座顶部。其模态振幅保持对称。

4 结语

本文通过对该型压力机进行了有限元建模并对其结构强度、刚度分析以及动态分析。结果表明大部分结构处于低应力区，结构还可以进行进一步优化。给出了该横梁结构的前十阶固有频率，为压力机动态分析提供了基础数据，并使压力机在工作时其工作频率远离各阶固有频率，以避免发生共振耦合。

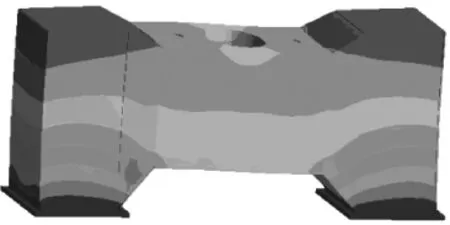
图7 压力机横梁第3阶模态振型

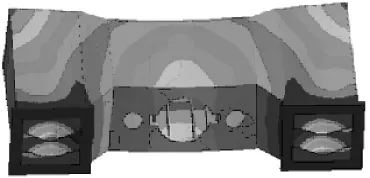
图8 压力机横梁第4阶模态振型

［1］刘强，付文智，李明哲，等．三梁四柱式多点成形压力机机架结构有限元分析和优化设计［J］．塑性工程学报，2003，10(5):49－52．

［2］谢峰，雷小宝，林巨广，等．C型压力机机身的有限元分析与优化［J］．机械工程师，2007(7):25－27．

［3］FRIEDEL H．Structural analysis with finite elements［M］．Springer-Verlag，2009．

［4］温秉权．金属材料手册［M］．北京:电子工业出版社，2009:103－105．

［5］WIJAVA C，YOON M C，KIM B T．Numerical investigation on the dynamic characteristics of an automotive A/C hose［J］．International Journal of Automotive Technology，2012，13(3):433－440．

［6］HE J，FU Z F．Modal Analysis［M］．Butterworth-Heinemann，2001．