一种低成本视差立体特效设计与实现

袁行远，苏 杰

(1．淘宝(中国)软件有限公司 广告技术部，北京 100026;2．山东科技大学 信息科学与工程学院，山东 青岛266510)

近年来，现代计算机图形学飞速发展，基于双目成像的立体特效技术越来越受到关注。看过立体电影、使用过可定位式光栅显示器和头戴式显示器(Head Mount Display)的人常被其逼真的效果所震撼，但其昂贵的价格却让人望而却步。本文提出一种用普通电脑屏幕实现逼真广视角的三维立体特效的低成本方法，实现了具有24位色，40°视觉范围和800×600的分辨率的三维特效。

1 视觉原理

1．1 大脑构建世界模型的视觉依据

大脑形成世界模型的时候综合了多种感官，通过它们，大脑可以得到物体和观察者的距离［1］，因此这些感觉也被称为深度线索［2］，其中，视差作为重要的深度线索不可忽略，如果在传统方法上协调地引入视差作为深度线索，可极大提高成像效果。

1．2 通过视差产生立体效果

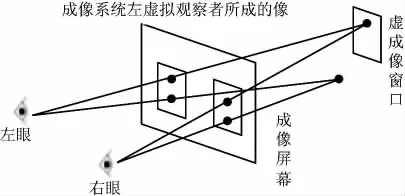
图1 用普通屏幕产生视差立体效果的设想

由于2只眼睛看到的图像不同，大脑由视差可以推测出光线射到双眼的角度，进而产生立体感。

笔者在屏幕上绘出2幅图像，如图1所示。如果能让左眼看到左边那幅，右眼看到右边那幅。就能欺骗眼睛看到屏幕后面的具有三维立体特效的物体。但不经过特殊训练，通常是不能直接看到视差产生的立体效果的，因为深度线索不止一个，要想成功给大脑创造“另一个世界”，就要尽可能平衡各种深度线索产生的距离感。

1．3 多种因素的协调判断

如图1所示，由焦距给出的距离认为图像在成像屏幕，而由视线分开的角度(2幅图分开的角度)得到的距离显示对应的像却成在虚成像窗口处。由视差(2幅图的不同)也可以得到一个距离，如果再加上透视关系产生的距离感，共有4个因素。如果由这4个因素得到的距离不同，大脑就无法正确构建出距离感。

笔者在改进的三维成像系统中证明并验证:适当调整成像系统参数可以使透视线索和视差线索判断出的距离相同。再用光学设备让焦距和眼球运动所得到距离一致，就能使多种因素协调，从而使普通人也能轻松看到三维立体特效。

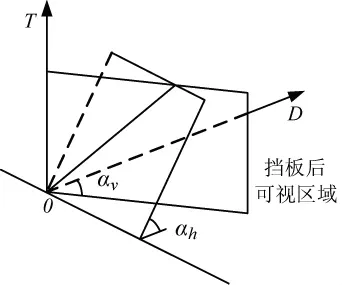
图2 观察者系统

2 改进的三维成像系统

2．1 简单透视成像引擎的数学描述

设观察者坐标为0，观察方向向量为D，头顶向量为T。αv是纵向视觉角度，αh是横向视觉角度，如图2所示:D只与方向有关而与长度无关，而D与T垂直，所以D和T向量只有3个自由度，由3个变量即可决定其全部性质。

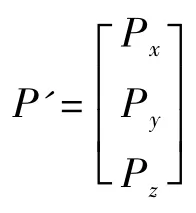
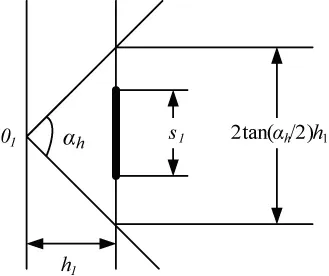
图3 绝对透视强度示意

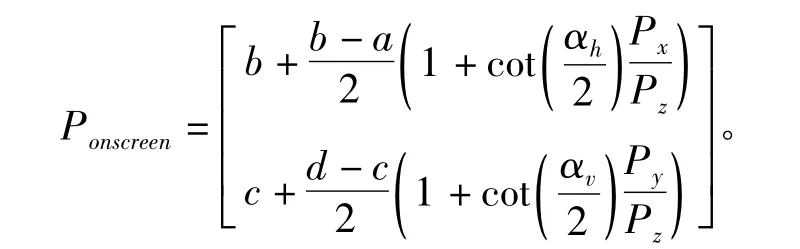
2．2 绝对透视强度

定义1:物体视角宽度αsee是指在观察一个物体时，物体在视野中的左边缘和右边缘到观察点的连线所成夹角。它刻画了物体在水平方向上在视野中所占角度。

定义2:绝对透视强度是简单透视成像系统的特征，记作Sα，其值为其中:αh为横向视觉角度，h1为屏幕到观察者的距离，s1为成像屏幕大小。

2．3 相对透视强度

定义3:相对透视强度Sr是双观察者透视成像系统的特征其中:dr是实际观察者(通常是人)的眼距，dv是虚拟观察者的眼距，αh为横向视觉角度，h1为屏幕到观察者的距离，s1为成像屏幕大小。

相对透视强度定理:用具有相对透视强度Sr成像系统描绘位于视野中心距离dpre＇物体时，实际观察者从图像透视关系得到的距离为dpre，从图像视差得到距离为ddiff，如果dpre=dpre＇，那么ddiff=dpre⇔Sr=1。

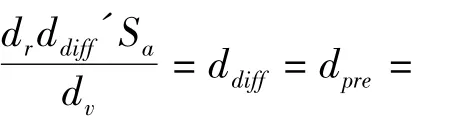
注1:Sr=1时，透视产生的纵深感等于视差产生的纵深感，此时计算机产生的图像与真实图像相同。图4是笔者的实证实验，证明了相对透视强度定理的正确性。

图4 sr=sa=1.2时的成像图像和照片的比较

2．4 成像系统参数的选取

立体照片的镜头分开距离依赖于拍摄的物体大小［3］。照片的大小s1已知，照相机的成像角度αr可测，观察距离h已知，实际眼距大约是6 cm，虚拟眼距就可以定量计算出来:dv=2tan(ar/2)hdr/s1。

分时眼镜、红绿眼镜、光栅显示器和立体电影成像大小为屏幕大小s1，实际眼距取6 cm，观察距离h1可测出，假设要把观测场景缩放为真实大小的m倍，可令dv=mdr，计算机虚拟成像系统的视觉角度理应定量计算出来:ar=2arctan［s1m/(2h1)］。

3 光学设备

3．1 焦距和视线夹角

观察无限远的物体，两眼自然分开注视的是正前方，视线的夹角为0，此时聚焦在无限远。若看大约20 cm外的屏幕时，视线的夹角是6°左右，此时聚焦在20 cm。

在屏幕上显示2幅大小为6 cm的图像。如果让左眼观察左边图像，右眼观察右边图像，那么视线夹角为0，但焦距却在20 cm。与前述常理不符。这就是一般情况下不能实现双目特效的主要原因。

为了消除这个不协调，在左右眼观察不同图像时，如果能把两幅图像重叠在一起，焦距和眼球观察的角度就和平时无异，也就平衡了两者所给出的纵深距离感。通过2次平面镜反射就能把两幅图像合二为一。

3．2 光路图

s1s2为实际屏幕，长度是32 cm。人的距离e1e2为6 cm，并假设观察距离为20 cm。0是屏幕中点，A1B1，c1d1，A2B2，c2d2是 4 块玻璃，均与水平方向成45°夹角。

由于屏幕大小s1s2=32 cm，为使观察图像分别平移到中间，e1＇和e1的水平间距应为屏幕的四分之一，为8 cm。又由于观察距离是20 cm，e1＇的位置就可以确定。由于光路平移了8 cm，而光线总传输距离和观察距离相等应为20 cm，所以实际眼镜的位置到实际屏幕的距离应为12 cm，e1就确定了。这样除了镜子的位置，其他都得以确定。为使靠近e1的镜子覆盖全部视野又不遮挡光路传播，放在距离e13 cm的位置。如此，光路图就可以以确定方式作出。

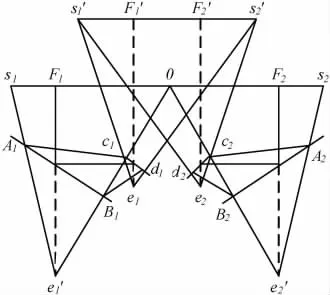
图5 成像设备原理

由左半屏幕s10向e1＇发出的光线，经过A1B1反射到c1d1，再汇聚到实际观察者的左眼。两边的反射使实际观察者看起来就像在看距离e1F1＇为20 cm的屏幕一样。

3．3 透视强度和图像分辨率

实际观察者眼距dr=0．6，横向视觉角度αh取60°，屏幕到观察者的距离h1=20 cm，成像屏幕大小s1=32 cm。为使Sr=1，可以确定此时虚拟观察者的眼距dv≈0．43。这时透视和视察产生的距离感是平衡的。

一个普通CRT屏幕的横向分辨率可以达到1 920×1 440和24位色，分屏后单个屏幕是960×1 440，因而笔者的成像设备确能达到800×600和24位真彩色。

4 程序和效果

笔者的项目主页位于 gnf3d．sf．net，软件可以从上面下载。

4．1 成像设备照片

图6是测试用的实际设备照片:自制双目潜望镜。

4．2 程序运行效果截图

图6 双目潜望镜

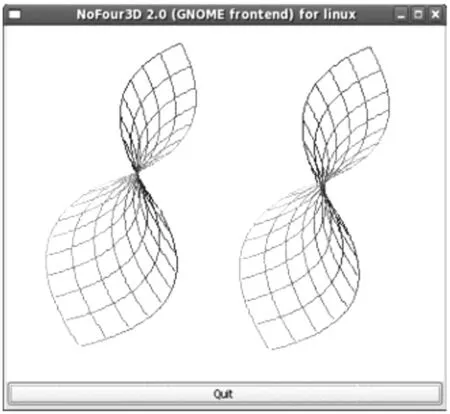
图7 旋转抛物面(笔者所作NoFour3D引擎绘制)

图8 太阳系(笔者修改Celestia软件后用OpenGL引擎绘制)

5 结语

40°的视觉范围是反射式成像设备的极限，引进折射可以从根本上改进现有的设备。相对透视强度定理和其在图4中的实景验证是笔者的成功之处，但仍欠缺在非视野中央的成像系统理论。希望以后能够有所改进。

［1］HAWKINS J，BLAKESLEE S．人工智能的未来［M］．贺俊杰，李若子，杨倩，译．西安:陕西科学技术出版社，2006．

［2］SIRLEY P．计算机图形学［M］．2 版．北京:人民邮电出版社，2007．

［3］汪明霓．视差立体图像及其实现算法［M］．北京:科学出版社，2005．

［4］王琼华，陶宇虹，李大海，等．基于柱面光栅的液晶三维自由立体显示［J］．电子器件，2008(1):296－298．