基于负载均衡和流量优先级的网络拓扑设计

李 富，程子敬，李 周，王 瑞

（北京卫星信息工程研究所 北京 100086）

为了提高网络可靠性，交换机连接为环型拓扑或网状拓扑，但会形成二层环路，IEEE STP生成树协议[1]通过有选择性地阻塞网络冗余链路来达到消除网络二层环路的目的。但STP导致负载分配不均和瓶颈，尤其在接近根交换机的位置。同时在没有经过优化的拓扑结构中，可能会存在较大传输时延。所以，良好的网络拓扑设计是避免网络时延影响的第一步。

网络拓扑设计问题作为一个复杂的组合优化问题，同样可归结为一个NP-hard问题。文献[2]提出可靠性和成本平衡的拓扑设计方法，但没有考虑交换机的容量限制。文献[3]采用遗传算法来优化子网划分，平衡各个子网的通信负荷。文献[4]研究了TS（Tabu Search）算法来优化交换式网络。文献[5]中利用模拟退火（SA）算法作为找到最佳网络拓扑结构的技术。

文中根据终端节点之间的业务优先级及其静态流量要求，提出了一种网络拓扑选择算法，确定交换机的生成树拓扑以及终端节点和交换机的连接关系。该方法对拓扑进行评分，在所有可能的拓扑结构中找到最好的拓扑结构，确定交换机之间的树型拓扑和终端节点的分布位置。在网络拓扑评估中考虑两条准则：交换机负载均衡，和流量最短路径选择。定义两个系数α，β分别对应上述准则，根据目标确定每个准则的权重。算法独立于上层应用，可以用来保证高优先级的业务流量经过最短路径，同时避免网络资源的利用不足。同时考虑到可靠性，可以将最好的拓扑进行结合，构造交换机之间的冗余网络拓扑。

1 网络模型

将网络建模为无向图 G（V，E），其中 V=｛v1，v2，…，vN，…vN+M｝，代表顶点集合，其中顶点{v1，v2，…，vN}对应网络的终端节点，{vN+1…vN+M｝对应交换机。 E=｛e1，e2，…，eN，…eN+M-1，｝代表边集合，其中{e1，e2…eN}对应终端节点和交换机之间的链路，{eN+1，eN+2…eN+M-1}代表交换机之间的链路。网络的节点和链路不发生故障。

交换机顶点{vN+1…vN+M｝和交换机之间的链路{e1，e2，…eM-1}，组成的G的子图G1，G1的邻接矩阵Tc=[Tij]有M行和M列，其中

Tc为对称矩阵。由于生成树中，边的数目为顶点数目减1，所以Tc中对角线以上非零元素为M-1。

节点 v1，v2， …，vN和 vN+1， …，vN+M存在着以下连接关系，vi=f（vj）（j=1，2，…，N；i=N+1，N+2，…，N+M），一个终端节点只能接到一个交换机上。交换机和终端节点的连接矩阵A=[Aij]有 1 行和 N 列，其中 Aij=vi（i=N+1，N+2，…N+M，j=1，…N），代表第j个终端节点连接到第i个交换机上。

子图G1的邻接矩阵Tc，及交换机和终端节点的连接矩阵A可确定唯一的网络拓扑。

2 基于业务优先级和负载均衡的拓扑设计

假设 Ci（i=1，2，…，N）表示第 i个节点（交换机）的交换能力，以 Gbps 为单位。 Dij（i，j=1，2，...，M，i≠j）表示终端节点 i和j的流量需求，也就是说，节点之间的平均用户流量，Mbps为单位。Pij（i，j=1，2，...，M，i≠j）表示终端节点 i和 j的流量的优先级要求，Pij的取值规则如下：

Pij值越大，表明从节点i到节点j的业务流量在优先级考虑中所占的权重越大。

此外，α，β（0≤α，β≤1，α+β=1）是用户定义的归一化参数，分别代表每条准则的重要性：交换机负载均衡（SLB），和流量最短路径（SPS）。例如，如果主要考虑交换机负载均衡，令 α=1，β=0，但如果同等考虑 SLB 和 SPS，令 α=β=0.5。

对于每种拓扑结构，在分配流量要求后，可以定义Si（i=1，2，...，N）为第 i个交换机的流量负载，以 Gbps为单位。

其中，path（m，n）表示流量 Dmn经过的路径，交换机负载为经过此节点所有流量之和。

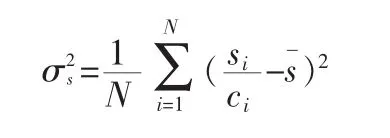
其中，

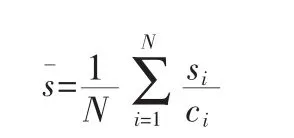
在SPS标准，其目标是找到一个最低L.的拓扑结构，这样可以保证高优先级的业务流量沿最短路径传输。

其中 pathcost（i，j）表示业务流量从节点 i到节点 j的交换机数目。

对于一个具有N个节点的网络，算法的输入参数是流量矩阵 D=Dij，i，j=1，...，N，i≠j，客户业务优先级矩阵 P=Pij（i，j=1，2，...，M，i≠j），和 α，β（0≤α，β≤1，α+β=1）。

算法如下：

1）M个交换节点全连接情况下，找到交换节点的生成树，并确定其邻接矩阵 Tc=[Tij]，i，j=1，...，M。

2）根据Tc，客户业务优先级矩阵 P，和流量矩阵 D，计算客户业务流量的平均路径长度L，和交换机的负载Si（I=1，2，...，N）。

3）基于SLB和SPS标准，为每种拓扑指定3个参数Sc1，Sc2

归一化这些参数，分别用Sc1，Sc2代表，

4）为SLB和SPS，分别指定系数α，β，并基于用户的目标找到最好的树形拓扑结构。要做到这一点，在第3步中获得的每个归一化参数乘以其相应的系数，并求和，

这样可以为所有可能的拓扑结构分级。此处，不考虑所有终端节点连接到同一台交换机的情况。选择得分最高的拓扑，作为最优拓扑，确定交换机节点之间的邻接矩阵Tc，及交换机和终端节点的连接矩阵A。

3 计 算

对于N个交换节点，M个终端节点的网络图G而言，图G1代表交换节点的全连接图，设A是图G1的关联矩阵，G1的生成树的数目 t（G1）=det（AAT）[6]。 对于终端节点 vj（j=1，2，...，M），f（vj）有 N 种取值，则图 G 的可能拓扑有 t（G）*MN种。当N和M值较大时，拓扑数量将非常巨大。因此采用遗传算法进行全局搜索。遗传算法进行拓扑选择的主要步骤如下。

1）编码 划分为M+1个子区间，第一个子区间为交换机的邻接矩阵，由邻接矩阵的对角线以上元素组成，其中非零元素个数为N-1，编码长度为N*（N-1）/2，随后为交换机和终端节点的连接矩阵A，划分为M个区间，每个子区间的取值范围为 [1，N]，即每台终端设备可能连接到N台交换机中的一台，每个子区间采用二进制编码，编码长度m，使得2m-1≤N-1≤2m-1。一种编码组合称之为一条染色体。染色体长度为L=N*（N-1）/2+M*m。

2）初始化种群 设置种群数目为20，采用随机初始化的方式，产生20个编码长度为L的合格染色体。区间1的编码要求任意两点间是连通的，可通过Floyd算法[7]进行验证。染色体的区间2到区间M+1的编码要求至少有两个区间的编码不相同，即排除所有终端节点连接到一台交换机的情况。

3）解码并鉴别 将染色体解码并采用线性鉴别模型进行鉴别，转换为真实值。

4）计算适应度 适应度等于目标函数值Final_score。

5）选择、交叉、变异 选择方法采用“轮盘赌”选择法。交叉概率设定为0.8，采用单点交叉算子，邻接矩阵作为一个整体其内部不进行交叉，随机交叉位置须在染色体第一个子区间之后，采用精英主义策略，保留最优解。变异概率前2/3繁殖代数设定为0.4，后1/3繁殖代数设定为0.1，如果第一个子区间内的基因发生变异，代表交换机的邻接矩阵发生变异，产生一个新的邻接矩阵。

6）重复 3），4），5）操作至繁殖到 60 代。

7）根据交换机节点的邻接矩阵和交换机和终端节点的连接矩阵A，确定网络拓扑。

4 仿真结果

通过MATLAB实现拓扑选择算法。其输入参数为一个具有M个终端节点的网络流量需求矩阵 D，元素为 Dij，i，j=1，2，...，M，（Dii=0）， 终端节点间流量优先级矩阵 Pij和 α，β（0≤α，β≤1，α+β=1）。 输出为分级的拓扑。

利用图1对算法进行说明

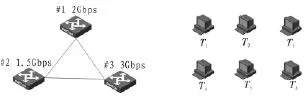
图1 网络节点Fig.1 Network element

图1中有3台交换机，形成全连接拓扑，交换机的交换容量[C1，C2，C3]=[2Gbps，1.5Gbps，3Gbps]，6 台终端节点设备，拓扑选择算法将确定交换机的生成树拓扑，并且将6台终端节点设备分配到3台交换机上。给出客户业务优先级矩阵和终端节点间的流量需求矩阵：

终端节点间的流量矩阵为

业务流量优先级矩阵

如果搜索交换机负载均衡最好的拓扑（SLB），则令α=1，β=0，得分最高的Tc及A如下：

交换机和终端节点的连接矩阵 A=[s3，s2，s3，s1，s2，s3]，（s1，s2，s3分别代表3台交换机）

网络拓扑如图2所示。

图2 基于SLB的最优拓扑Fig.2 Best topology based on SLB

如果搜索业务流量平均路径长度最短的拓扑 （SPS），则令α=0，β=1，目标是寻找具有最小L的拓扑，得分最高的Tc及A如下：

交换机和终端节点的连接矩阵 A=[s1，s3，s3，s1，s1，s3]，（s1，s2，s3分别代表3台交换机）

拓扑如图3所示。

图3 基于SPS的最优拓扑Fig.3 Best topology based on SPS

搜索过程中，交换机负载方差σ2s的最大值为0.246 56，最小值为9.63E-05。流量的平均路径代价L最大值为3，最小值为1。可见，不同的拓扑设计对参数的影响差异较大。

表1对比了基于SPS和SLB标准的拓扑中的交换机负载方差（σ2s）和流量的平均路径代价（L）。可以看到，SLB的交换机负载平衡性能优于SPS，SPS业务流量的平均路径长度小于SLB中的路径长度。

表1 基于SLB和SPS的拓扑性能比较Tab.1 Perform ance com parion of topology based on SLB and SPS

拓扑设计中，可综合考虑交换机负载平衡性能和业务流量的平均路径长度这两条准则，确定合适的α，β，平衡两方面性能。

5 结 论

文中引入了一个新的图论方法，定义了两个准则：交换机负载平衡、流量最短路径以及对应于上述两个准则的系数。首先，根据设计目标确定α，β的值，再利用业务流量优先级矩阵和静态流量需求矩阵作为输入，对所有可能的网络拓扑结构分级。设计具体的遗传算法时，利用交换机连接的邻接矩阵和终端节点和交换机的连接矩阵作为染色体，搜索全局最优拓扑。该算法独立于上层应用，避免了个别交换机负载过重，同时保证高优先级流量能够沿最短路径传输。航天器进行网络拓扑设计时，可综合考虑两条准则，寻找最优的拓扑或者对已设计的拓扑进行比较选择，确定航天器内交换机和终端设备的分布。

[1]IEEE Std 802.1W 2001.Media Access Control （MAC）Bridges Amendment 2：Rapid Reconfiguration[S].2001.

[2]Estepa，Rafael.A Productivity-Based Approach to LAN Topology Design[J].IEEE Communications Letters，2011，15（3）：349-351.

[3]胡晓娅，朱德森，汪秉文.用改进的遗传算法设计交换式工业以太网拓扑[J].计算机工程与科学，2007，29（9）:9-11.HU Xiao-ya，ZHU De-sen，WANG Bing-wen.Using improved genetic algorithms to design switched industrial Ethernet topology[J].Computer Engineering&Science，2007，29（9）:9-11.

[4]Pierre，S，Elgibaoui A.Improving communication network topologies using tabu search[M].Local Computer Networks，1997.

[5]Deeter D L，Smith A E.Heuristic optimization of network designconsidering all terminal reliability[C]//Proceedings of the Reliability andMaintainability Symposium，1997:194-199.

[6]陈勇，胡爱群.通信网中最重要节点的确定方法[J].高技术通讯，2004，14（1）:21-24.CHEN Yong，HU Ai-qun.A method for finding the most vital node in communication networks[J].Chinese High Technology Letters，2004，14（1）：21-24.

[7]刘焕淋，陈勇.通信网图论及应用[M].北京：人民邮电出版社，2010.