复合材料层合壳体热弹耦合简化模型
2012-06-08钟轶峰余文斌张亮亮
钟轶峰,陈 磊,余文斌,张亮亮
(1.重庆大学a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆400045;2.美国犹他州立大学 机械与航空航天工程系,洛根84322)
近20年来,先进复合材料结构因其高强度、高模量、可设计性等优点已广泛应用于航天航空、机械、土木等领域。由于复合材料不同成分、不同纤维方向的热膨胀系数相差很大,相比于各向同性材料对温度的改变更加敏感,复合材料板/壳结构的热响应已成为近年来复合材料力学热点课题之一[1-2],出现了各种复合材料板/壳理论。Ng等[3]应用古典层合理论(CLT)分析了复合材料圆柱壳的热残余应力和自由振动,由于忽略了横向剪切效应,该理论仅对薄壳有效;为克服CLT的缺陷,Pradyumna等[4]基于一阶剪切变形理论(FOSDT)分析了复合材料层合壳体在热环境下非线性动态稳定性,但模拟弯曲时数值计算结果严重失真,产生“横剪自锁”现象,其原因在于总应变能中包含横向剪切应变能的项在量级上不正确,沿厚度方向变化的剪切应变线性假设与上下表面剪应力为零自相矛盾,需人为地引入与几何形状和材料相关的剪切修正因子来解决这一矛盾;为提高沿厚向的应力/应变预测精度,各国学者纷纷把研究重点转向了高阶剪切变形理论,Li等[5]用高阶壳理论分析了复合材料圆柱壳在热环境下的非线性屈曲和后屈曲性能,Nosier等[6]基于层合理论确定湿热环境下正交铺层/角铺层壳体的局部位移函数和层间应力,但仍无法准确预测面内的不连续性和沿厚度方向的横向位移分量。
由上述分析可知,现有板壳热弹性分析理论大多基于位移场假设,无法较好地反映层合板壳的三维效应和铺层之间的相互作用。笔者尝试采用变分渐近法[7-8]分析层合圆柱壳的单向耦合热弹性问题。通过对降维模型近似能量中变分项的渐近修正,得到与原三维能量尽可能接近的近似能量,从而构建一种无需先验性假设且便于工程应用的简化壳体模型,为复合材料层合壳体在工程中的实际应用提供有价值的参考。
1 复合材料层合壳体三维能量表达式
基于Hamilton扩展原理,三维结构的弹性动力性能可表述为

式中:t1和t2是任意两固定时间;K和U分别是动能和Helmholtz自由能;δ¯W是外力所做虚功,上划线表明不需要对该项精确变分。

图1 层合壳体几何构型及坐标系
由于仅考虑单向耦合热弹性问题,因壳体变形引起的温度改变忽略不计,得到无二次项的Helmholtz自由能泛函[9]:
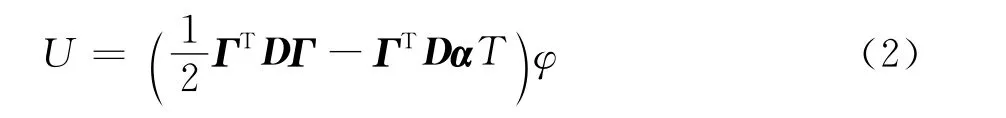
式中:D为6×6阶三维材料矩阵;α为6×1阶三维热膨胀系数列阵;T为相对于零应力状态的温差;为壳体几何修正系数,其中kαβ为壳体面外曲率,因选用坐标系为图1所示曲率线,k12=k21=0。
Γ为三维应变场[10],可定义为
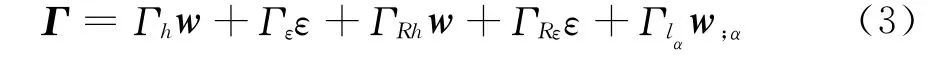
式中:为相应的算子;

其中:εαβ,καβ统称二维广义应变,其阶数分别用n,n/h表示;w i为未知翘曲函数,若将参考面定义为壳体中面,则w i须满足如下3个约束

壳体参考面上质点的动能和外力所做虚功可分别表示为

式中:μ为质量密度;U i为沿坐标轴x i的位移,其上的点表示对时间求导;=-δU3;α为虚拟旋转;广义力f i和力矩mα可定义为

式中:p i,τi,βi分别为体力、壳体顶/底面表面力。
由式(1)、(6)和式(7),壳体参考面的动力性能可改写为
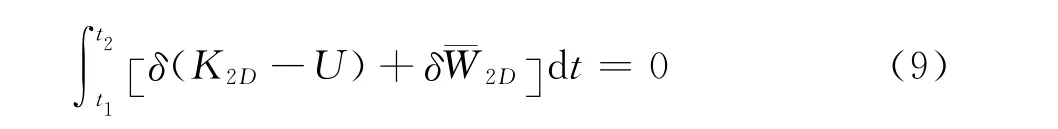
由于式(9)中存在未知翘曲函数w i,若直接求解该式,将会遇到与求解原三维问题同样的困难。常规做法是对翘曲场作先验性假设,由于复合材料的各向异性和非均质性,这种假设可能会产生较大的误差。变分渐近法可利用壳体固有的小参数对式(9)的变分项进行渐近分析得到w i,从而构建与原三维模型尽可能接近的二维壳体模型。
2 降维方法及近似能量推导
对壳体结构,可选择h/l≪1,h/R≪1作为变分渐近计算所需的小参数,由此可估计各荷载阶数为

式中μ为弹性材料常量的阶数。
利用h/l,h/R可将三维能量渐近扩展为如下形式的系列二维近似能量泛函
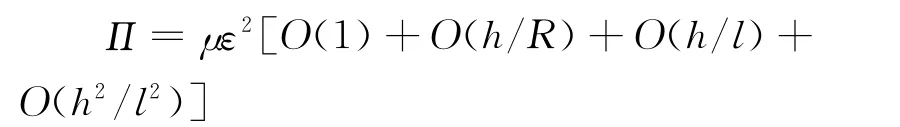
为能处理体多层壳结构,并与二维有限元求解器相衔接,可将三维翘曲场离散为一维有限单元形式,
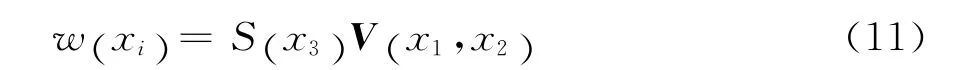
式中:S为形函数;V为沿横法线方向的翘曲场节点值。
将式(11)代入式(9),得到离散形式能量泛函为

式中:L为荷载相关项;新引入的与几何形状和材料属性有关的变量为

式(5)翘曲约束的离散形式可表示为

式中:H= [STS];ψ为零初始曲率E0的正交化核心矩阵,ψTHψ=I。这样,未知翘曲函数的求解问题转化为式(14)约束下式(12)最小化问题。
2.1 零阶近似
应用变分渐近法,需根据不同阶数找到泛函的主导项。式(12)中与未知翘曲函数有关的零阶近似主导项为

式中:E0,D hε0,Dεε0,αh0,αε0分别由式(14)中φ=1(无几何修正)定义的相关矩阵。
相应的零阶翘曲函数为

将式(16)代入式(15)得到渐近修正到O(1)阶的能量泛函为
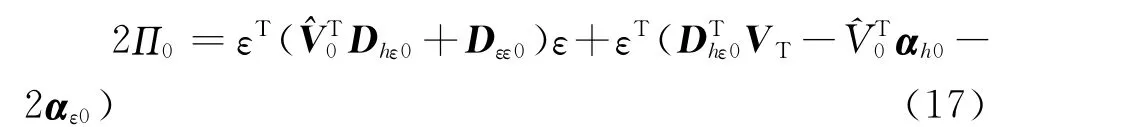
这与如下形式的热弹性古典层合模型相一致,

式中:A,NT分别为二维刚度矩阵和温度产生的应力合力,其计算式为

2.2 一阶近似
零阶近似可用于分析薄壳的全局性能和面内分量,更高阶近似可用来分析对中厚壳失效十分重要的面外应力和应变(σi3,Γi3),从而构建更精确壳体模型。
首先,将能量泛函渐近修正到O(h/R)阶以考虑初始曲率效应,O(h/R)阶翘曲因对能量无贡献,可不必计算。得到

式中:

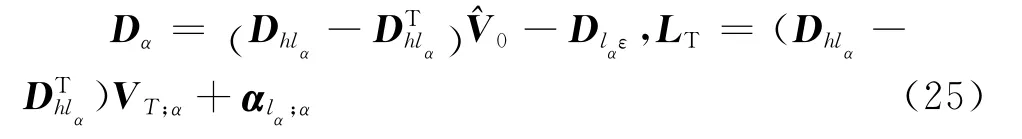
其中带星矩阵由φ-1代替式(14)的φ定义。
其次,将能量渐近修正到O(h2/l2)以考虑横向剪切变形。为此,将零阶翘曲函数摄动为

将式(23)代回式(17),可得到一阶近似的总能量泛函主导项为

式中:
相应的一阶翘曲可求解为

最后得到渐近修正到O(h2/l2),O(h/R)的总能量泛函为

式中:
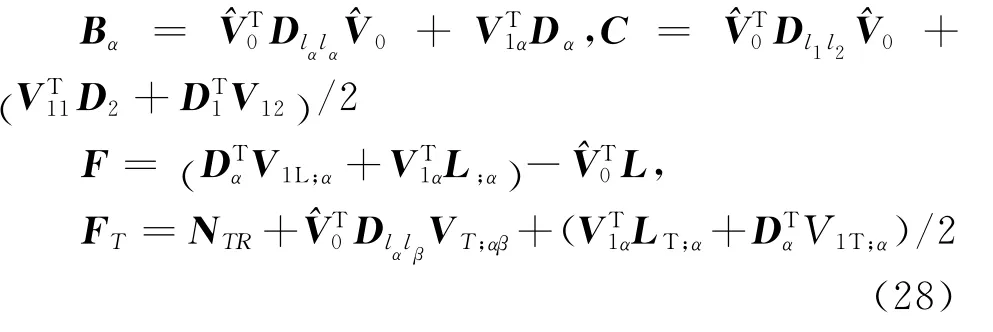
2.3 近似能量转换及三维场重构
尽管式(27)能量泛函渐近修正到O(h2/l2),O(h/R)阶,但因含有广义应变的导数ε;α,难以直接应用。为得到实用的能量范函,可将式(27)转换为工程中常用的Reissner-Mindlin模型形式。
在Reissner-Mindlin模型中有两个附加横向剪切应变Reissner-Mindlin模型应变量R与ε的关系可表示为

式中:
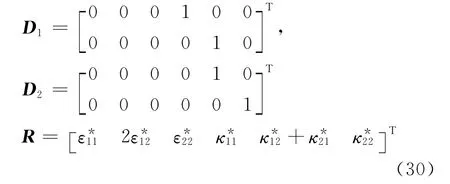
将式 (29)代 入 式 (27),可得到 由 Reissner-Mindlin应变量表示的能量泛函为

而实际应用的广义Reissner-Mindlin模型形式为
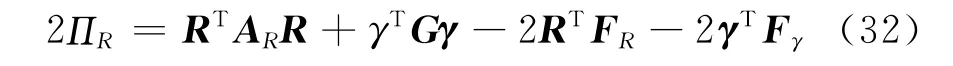
为得到与式(32)等效的 Reissner-Mindlin模型,可通过以下2个弯矩平衡方程消除所有二维应变量的偏导数

由式(33),可将式(31)改写为
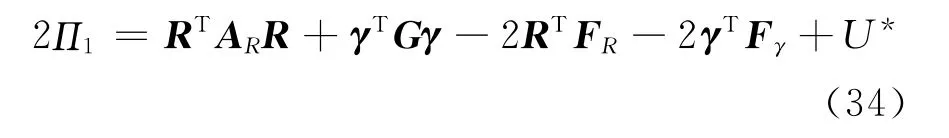
式中:
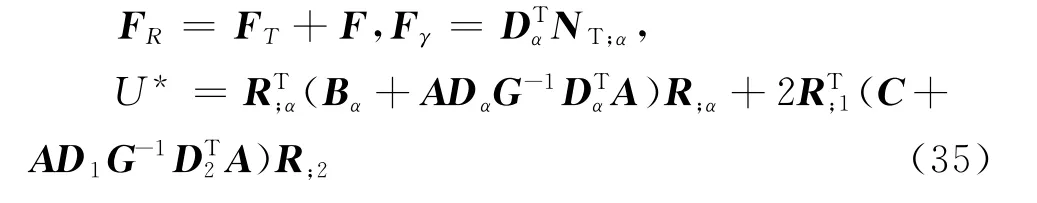
若对任何R,U*都趋于零,则可得到渐近修正Reissner-Mindlin壳体模型。对于一般各向异性壳体,该项往往并不为零,可通过最小二乘法等优化技术最小化U*,等效Reissner-Mindlin模型的精确性取决于U*趋近于零的程度。
由于降维模型的可靠性最终取决于其对三维场预测的精确度,因此还需提供重构关系以完善降维模型。由式(3),重构的三维应变场可表示为

三维应力场可使用材料本构关系得到,

3 算例
柱形弯曲问题已作为评估新提出的3D/2D分析模型精确性的基准。本章将所述理论和方法编制成变分渐近板/壳分析程序VAPAS,对图2所示4层简支复合材料层合壳体在热/载荷下的柱形弯曲问题进行分析。

图2 层合壳体结构示意图
3.1 模型参数
壳体 各 层 倾 角 为 [90°/0°/90°/0°];壳 厚h=1 mm,半径R=10 cm,夹角φ=π/3;采用的坐标系为x1∈ [0,φ],x2∈ [0,∞],x3∈ [-h/2,h/2];材料为石墨/环氧复合材料,材料属性为

壳体承受的温度变化和正弦面荷载分别为

3.2 数值分析与讨论
图3(a)~(f)绘出了重构的沿厚度方向应力分布,并与一阶剪切变形理论(FOSDT)、古典层合理论(CLT)和精确解[11-12]进行对比。应变和位移的变化趋势和精度与应力相同,限于篇幅未在此绘出。由于应力分量σαβ,σ33分别是正弦和余弦函数,应力分布分别绘于x1=π/6和x1=π/3处。为方便比较,图中纵横坐标分别正则化为

由图3可看出:VAPAS、FOSD和CLT都能较准确地预测面内应力分量σαβ分布,由于VAPAS能得到优化剪切刚度矩阵G,其结果比FOSDT和CLT更精确;对于横向应力分量σα3,因特殊的铺层设计(正交铺设),CLT无法计算该值,而FOSDT因对位移场所做先验性假设,误差较大,VAPAS与精确解相一致,且重构的应力分布在不同层分界面处连续,这与大多数位移基壳理论完全不同。

图3 4层简支复合材料圆柱壳体在热/载荷下沿厚度方向的应力分布
4 结论
1)基于变分渐近法构建了复合材料圆柱壳热弹性简化Reissner-Mindlin模型和重构关系,可考虑热/载荷单向耦合效应,并使用4次多项式表示沿厚度方向的任意温度分布,相较于假设温度沿厚度方向线性分布(单层板理论)或沿层线性分布(层合理论)更符合实际情况。
2)在推导降维模型过程中,使用变分渐近法求解未知翘曲函数,不需任何动力学假设和剪切修正因子,也不同于传统的板/壳理论假设翘曲场的一般形式,用高阶翘曲作参数来求解假设函数中的未知参数的方法。
3)通过算例验证:重构的沿厚度方向应力分量与三维精确解吻合很好,且简化模型为等效单层壳模型,计算量与一阶剪切变形理论相当,若壳体层数增加,其高效性更加显著。
[1]Shen H S.Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part II:pressure-loaded shells[J].Composite Structures,2011,93(10):2496-2503.
[2]Li Z M,Yang D Q.Thermal postbucking analysis of 3D braided composite cylindrical shells[J].Journal of Mechanics,2010,26(2):113-122.
[3]Ng T Y,Lam K Y,Reddy J N.Dynamic stability of cross-ply laminated composite cylindrical shells [J].International Journal of Mechanical Sciences,1998,40(8):805-823.
[4]Pradyumna S,Gupta A.Nonlinear dynamic stability of laminated composite shells integrated with piezoelectric layers in thermal environment[J].Acta Mechanica,2011,218(3/4):295-308.
[5]Li Z M,Lin Z Q,Chen G L.Nonlinear buckling and postbuckling behavior of 3D braided composite cylindrical shells under external pressure loads in thermal environments[J].Journal of Pressure Vessel Technology,2009,131(4):258-269.
[6]Nosier A,Miri A K.Boundary-layer hygrothermal stresses in laminated,composite,circular,cylindrical shell panels[J].Archive of Applied Mechanics,2010,80(4):413-440.
[7]Pinhas B Y.New variational-asymptotic formulations for interlaminar stress analysis in laminated plates[J].Journal of Applied Mathematics and Physics,1986,37(8):305-321.
[8]Lee C Y.Dynamic variational asymptotic procedure for laminated composite shells:part I:low-frequency vibration analysis[J].Journal of Applied Mechanics,2009,76(9):110-122.
[9]Reddy J N.Mechanics of laminated composite plates and shells,theory and analysis[M].2 ed.CRC Press,2004.
[10]钟轶峰,余文斌.用变分渐近法进行复合材料层合板仿真及三维场重构[J].复合材料学报,2010,27(4):174-179.ZHONG Yifeng,YU Wenbin.Simulation and 3D field recovery of composite laminated plates by use of variational asymptotic method [J]. Acta Materiae Compositae Sinica,2010,27(4):174-179.
[11]Ren J G.Exact solutions for laminated cylindrical shells in cylindrical bending [J].Composite Science and Technology,1987,29(3):169-187.
[12]Jing H S,Tzeng K G.Elasticity solution for laminated anisotropic cylindrical panels in cylindrical bending[J].Composite Structures,1995,30(4):307-317.
