砂土介质中土压力盒的力学响应特性
2012-08-11刘先珊董存军
刘先珊,董存军
(重庆大学a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆400045)
土压力盒由于能直接反映土压力变化而在路基、挡土墙、坝体及隧道工程测试中得到了广泛的应用。但实际砂土介质为非弹性体,而且土压力盒与土体的刚度很难匹配,土压力盒附近产生应力集中或土拱效应而改变砂土体内的自然应力场。为了更好地运用土压力盒进行现场压力的准确测试,国内外许多学者对现场实测进行研究,Naoki等[1]对高压土压力盒进行研究,使土压力测试进入高压阶段;陈春红等[2]、李贯军等[3]研究了土压力盒运用于工程实测的几种原则;Ther oux等[4]为避免现场土压力盒埋设时产生刚度匹配,使用之前对其进行室内标定试验,找出合理参数运用于工程实际;Joseph等[5]根据实验和理论分析,说明不同类型的土压力盒在不同的边界条件下都会产生不同的试验结果;Zhu等[6]通过试验描述了砂土介质中土压力盒响应的非线性和迟滞性,指出不同类型的土压力盒与加载历史和应力环境相关。
上述试验方法的直观性为工程实测提供了便利,但试验条件和试验成本的限制以及介质的外界扰动会对土压力盒实测的有效性产生重要的影响。随着对实际土压力性状研究的不断深入,认识到砂土介质是大量离散颗粒相互作用而组成的复杂体系,呈现出非线性、弹塑性、剪胀性和流变性等。现有的宏观岩土力学理论和连续介质方法无法准确解释颗粒间的力学行为,而细观力学方法[7]-颗粒流方法(Particle Fl ow Code,PFC)为解决该问题提供了重要的研究手段。Chareyre等[8]基于改进的离散元方法模拟颗粒接触的力学行为,得到土颗粒与嵌入体的接触关系;Jiang等[9]运用颗粒离散元法模拟了砂土介质中嵌入仪的力学特性,其中土颗粒与嵌入仪的摩擦系数影响最为明显;Orianne等[10]运用PFC2D研究了土体颗粒摩擦系数、接触刚度以及孔隙率对嵌入体力学响应的影响规律;Zhou等[11]和Pradip等[12]从不同角度研究了颗粒性状对砂土-嵌入体的作用关系。那么,土压力盒作为一种嵌入砂土介质中的测试仪器,外力作用、介质颗粒大小、介质孔隙率、颗粒摩擦系数、压力盒自身特性以及测试环境等都会对土压力盒测值产生影响。因此,为了运用土压力盒进行更准确的测试,基于颗粒流数值方法来模拟实际砂土介质中的土压力盒力学响应成为一种新的研究思路。笔者通过建立的数值模型分析颗粒运动以及颗粒接触形成的力链网络和压力盒的力学响应,验证数值模型的可行性,并研究加载模式、颗粒松散程度、颗粒间摩擦系数以及压力盒刚度等对测量值的影响。
1 土压力盒力学响应数值模型
1.1 颗粒流数值方法
基于离散单元法的颗粒流数值方法[7]是通过模拟颗粒运动及其相互作用来研究颗粒体系的力学特性,并基于非连续数值方法来求解含有复杂变形模式的实际问题。砂土体[13]的离散特点决定了加卸载过程中介质应力的不确定性和复杂性,无法建立统一的、合适的连续介质模型。颗粒流方法的提出为砂土介质力学特性的研究提供了一种新的研究思路。随着计算机技术的逐步增强,颗粒模型模拟整个实际工程成为可能,一些细观特性可以在模型中自动形成,因此该方法能很好地再现岩土介质的细观力学特性[11]。笔者采用的Hertz-Mindlin接触模型[14],是根据 Mindlin和Cundall理论近似得出的一种非线性接触模型[7]。
1.2 数值模型验证
根据土压力盒实验,建立如图1所示的数值模型,对应模型的计算参数如表1所示,模型包含10 000个颗粒,其颗粒分区和对应的颗粒数如表2所示。压力盒设计为自由变动形式,如图2和图3所示。为了保证加卸载过程的平衡状态,压力盒顶部和底部在加卸载过程中保持竖直方向移动,荷载作用于模型的顶板上,加载卸速度为0.02 mm/s。
基于上述数值模型模拟了不同荷载作用下的土压力盒力学响应。图4~7为不同荷载的颗粒接触图形,显示了毗邻颗粒接触形成的诸多传递外荷载的路径:力链。若干力链形成网络[15]贯穿于颗粒体系内,决定着颗粒体系的宏观力学性能。而且,局部颗粒的受力大小不同促使力链网络结构形成强力链和弱力链。图4~7可以看出外荷载作用下,不同位置的颗粒受力不同,顶部颗粒的受力要小于底部颗粒的受力,随着外荷载的增加,颗粒产生变形,其接触力越大[16],压力盒顶部就形成较强的力链结构,此位置显示的应力集中也越明显。同时,还通过图8说明了加卸载过程中整体模型与压力盒的顶部、底部的力-应变变化过程。该图显示加卸载曲线不重合,完全卸荷之后一部分应变不可恢复,形成滞回环[17],说明砂土体自身的非线性特性以及加卸载过程中压力盒测试的迟滞性。另外,图9描述了砂土介质中压力盒的应力响应,其值与理想曲线偏差较大。主要在于初始压力盒系数由气标或油标得出,试验过程压力盒受力均匀,得到的压力盒应力为线性变化。而砂土介质与气、油性质不同,且试验条件以及对砂土体的扰动都会改变压力盒的测试结果,非线性加卸载曲线使得传统的最小二乘法[2]线性拟合得到的压力盒系数将不准确,那么只有准确标定后的压力盒才能进行有效监测。因此,可以在掌握砂土性质的基础上对埋入的土压力盒进行数值试验来获得压力盒的应力值,以此确定压力盒系数将是一种有效的方法。
上述研究成果可以看出,土压力盒的力学响应符合砂土介质力学特性的一般规律,由此说明笔者采用的颗粒流数值分析模型是可行的,可以运用该模型对后续的多因素影响土压力盒力学特性进行研究。

表1 颗粒流数值模型计算参数
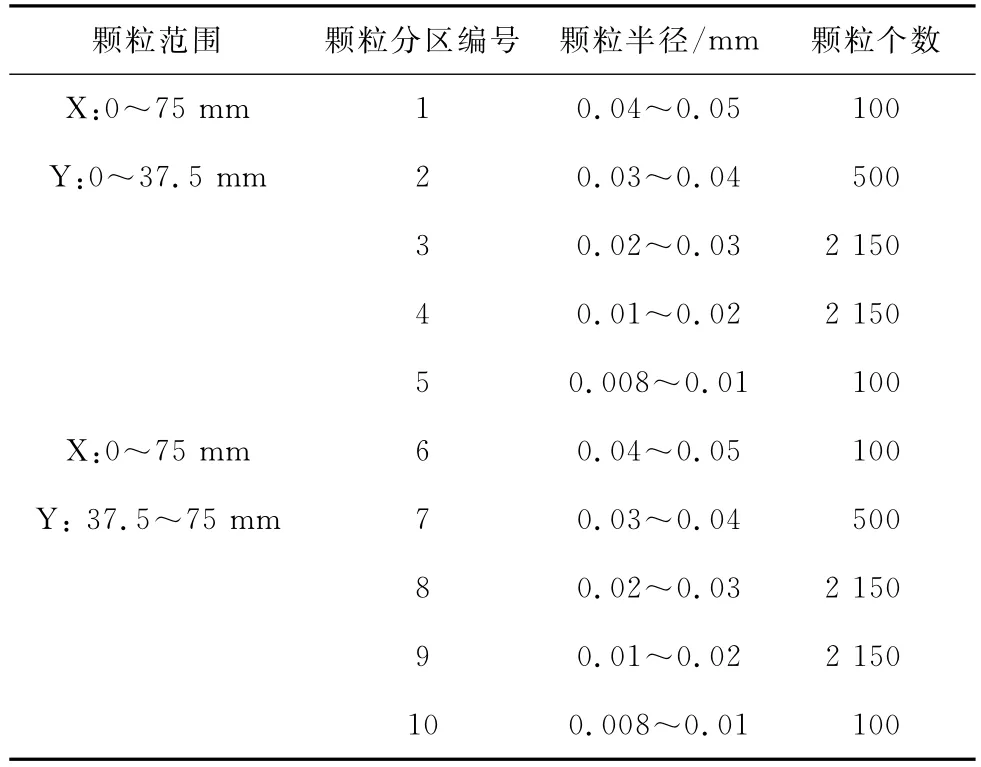
表2 不同范围的颗粒信息

图1 压力盒力学响应的颗粒流数值模型

图2 压力盒初始状态

图3 数值计算过程中的压力盒变化状态

图4 加载5 N时的颗粒接触图

图5 加载10 N时的颗粒接触图

图8 加卸载时的颗粒模型和压力盒力学响应
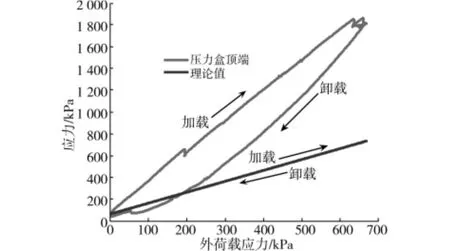
图9 土压力盒力学响应的数值模拟与理论值比较
2 土压力盒力学响应特性分析
2.1 荷载模式对土压力盒响应的影响
不同荷载模式对砂土介质中的土压力盒力学响应的影响不同,图10为循环加卸载过程中的整体模型与压力盒的顶部、底部压力-应变曲线,说明不同量级的荷载循环其力学特性不同,多次循环后的不可逆变形逐渐加大。从细观角度可知,在一个加卸载过程结束时,模型的尺寸会减小,开始另一个新的循环过程,加载中的颗粒会从当前位置开始少量移动。在移动过程中,切向弹簧拉长超过弹簧极限值,颗粒发生滑动;卸载时,颗粒趋向于返回初始位置,切向弹簧松弛,出现过滑动的颗粒由于在恢复过程中未达到弹簧极限值,其中的一些颗粒就会与邻近颗粒接触产生相互作用,颗粒与颗粒之间的距离越近。因此,不断的加卸载就会导致颗粒不断重组和压缩,孔隙减小,产生滑动而未能恢复到初始位置的颗粒越来越多,完全卸荷以后的不可逆变形也越来越大。另外,图形还显示随着荷载的增加,颗粒之间的空隙减小导致没有足够的空间允许颗粒重组和滑动,由迟滞曲线[17-18]的闭合区域面积可知整个加卸载过程中的能量消散减少,对应的应变逐渐增加。
图10显示的加卸载曲线具有较大的滞回环,说明加卸载过程中压力盒具有迟滞性。主要因为埋置于砂土介质中的土压力盒是由金属材料制成,迟滞性大小与材料本身的稳定性、均匀性、热处理后的金相组织等都有很大的关系。因此,土压力盒的实际运用中,可以通过不同的热处理方式提高弹性极限以减少迟滞性,另外选择传感器时应充分考虑迟滞性的自补偿,使其对土压力盒测量值的影响减到最小。
2.2 颗粒松散程度对土压力盒力学响应的影响
由于内部颗粒排列不同,砂土试样的孔隙率不同,受力过程中的颗粒运动不同,反映在压力盒上的力学效应也不同。考虑2种不同的孔隙率试样,松散型颗粒初始孔隙率:0.249,压密型颗粒的初始孔隙率:0.208,其数值计算结果如图11~13所示。图11可以看出两种类型的颗粒模型都表现出了相似的力学响应,对于初始孔隙率大一些的试样,孔隙率逐渐减小趋向于压密状态而形成颗粒接触,孔隙率越大,在荷载作用下达到相同的变形需要的时间更多一些,土压力盒的力学响应要慢一些。图12为荷载作用下压力盒顶部的应力-应变曲线,孔隙率大的颗粒应变要大于孔隙率小的颗粒应变,同样也说明了松散颗粒在挤压过程中就产生了较大的变形。图13对土压力盒监测值和理论值进行比较,并给出了测量值的线性表达式以模拟压力盒在不同荷载作用下的变化趋势。该图形显示孔隙率大的试样其测量值要小一些,说明孔隙率大的颗粒在荷载作用下有一个压密的过程,要达到相同测量值需要的外荷载就更大一些;另外土压力盒的测量值比理论值要大,主要在于颗粒刚度较大更易吸收外界荷载,更有效地形成力链网络将外荷载传递给土压力盒;同时还说明最小二乘法拟合的线性曲线与土压力盒实际应力响应值存在一定的误差,要获得实际工程中的土压力盒有效测值,就需要结合试验和数值方法组合分析来确定更为准确的土压力盒系数。
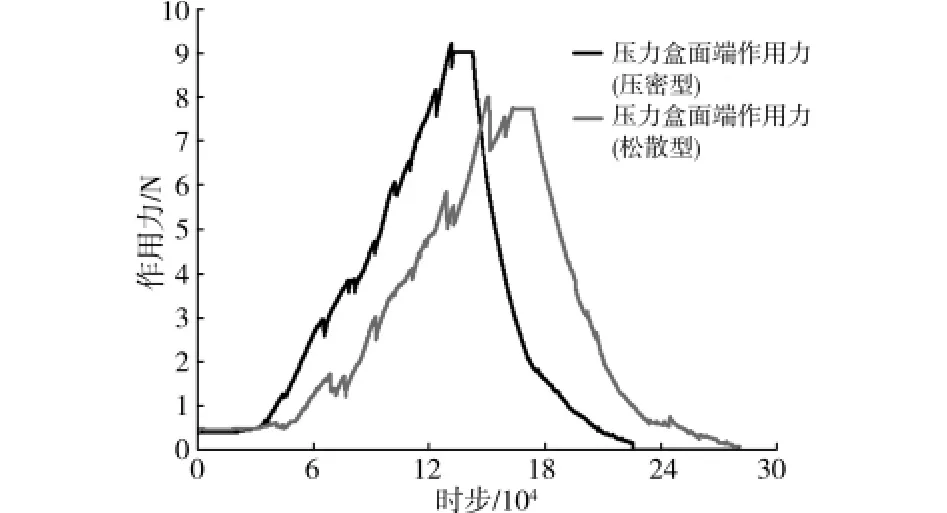
图11 不同孔隙率试样的土压力盒顶部作用力
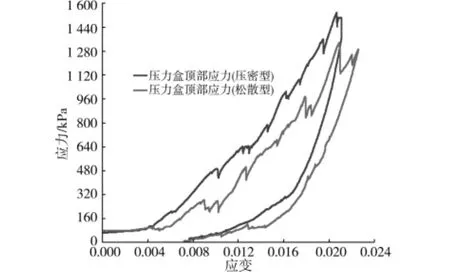
图12 不同孔隙率试样的压力盒顶部应力-应变关系
2.3 颗粒摩擦系数对土压力盒力学响应的影响

图13 不同孔隙率试样的数值模拟与理论值比较
颗粒本身的力学性质同样决定荷载作用下的压力盒力学特性,颗粒间摩擦系数不同其颗粒之间的接触力也不同,那么反映在土压力盒上的作用力也不同,其研究成果如图14所示。该图表明颗粒摩擦系数越小,土压力盒的压力-应变曲线表现出的迟滞性越强,这也说明颗粒之间的摩擦系数越小,颗粒之间的接触力越大,越容易产生变形,得到的变形量也较大,在卸载过程中的不可逆变形也越大。因此,选择土压力盒进行砂土介质应力测试时,需要在砂土介质实际勘测的基础上进行理论分析,并选择对应的土压力盒来减少测试曲线的迟滞性以保证监测值的准确性。
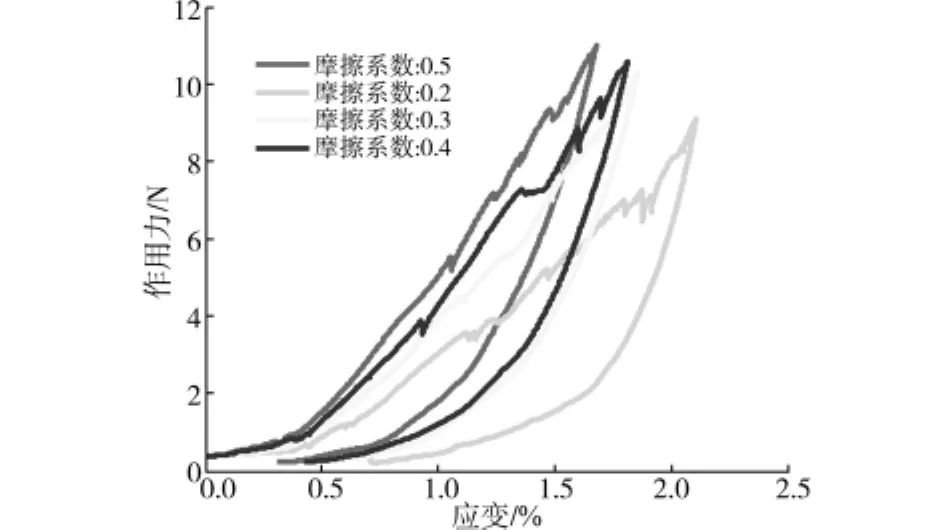
图14 不同摩擦系数影响的压力盒顶部作用力-应变图
2.4 压力盒刚度对土压力盒力学响应的影响
由于实际砂土体与土压力盒的刚度很难相等,土压力盒附近就会产生应力集中或拱效应而破坏砂土原来应力场。如果压力盒的刚度大于砂土体颗粒的刚度,则测量值偏大,反之测量值偏小。因此,压力盒刚度的选择对测试值的影响很大,其研究成果如图15和图13所示。其结果显示当土压力盒的刚度大于50 k N/m,其压力盒的力学响应模式相同,且力-应变曲线相差不明显,而对于刚度为0.5 k N/m的压力盒,由于压力盒刚度相对颗粒刚度要小,压力盒测试的力-应变曲线要小于理想值。主要在于对于刚度较大的压力盒更容易吸收外力,则作用在压力盒上的作用力要大一些,也即测量值大于理论值。因此,在实际测试工程中,要对砂土颗粒刚度和压力盒刚度进行比较研究,然后选择合适刚度的土压力盒,同时还要提高土压力盒的埋置要求并保证压力盒周围土体的密实度,由此提高土压力盒和砂土介质之间的刚度匹配。

图15 压力盒不同刚度影响的作用力-应变图
3 结论
砂土介质颗粒体系所具有的非连续和强接触耗散等结构使其呈现出非线性、弹塑性、剪胀性和流变性等复杂的力学特性,传统的宏观连续介质方法无法准确表述其复杂特性。因此,基于细观力学方法的颗粒体系精细力学行为研究砂土介质力学性质提供了新的思路,采用颗粒流数值方法从细观角度对土压力盒的力学响应进行研究。
1)研究了荷载作用下的颗粒接触、传力过程以及力链网络,说明了砂土介质受力过程中的力链是以骨架为基础的,颗粒骨架变形必然导致力链结构发生变化,其变化更精细地反映了颗粒体系和土压力盒对外荷载的响应。
2)基于颗粒流数值模型得到的力-应变曲线符合一般规律,由此验证了笔者提出的颗粒流模型是可行的;并比较了加卸载过程中土压力盒应力变化曲线与理想曲线,说明介质特性对压力盒力学响应和压力盒标定具有重要影响,为后续土压力盒力学响应分析奠定了研究基础。
3)加卸载模式、试样松散程度、颗粒摩擦系数以及压力盒刚度对压力盒响应有着不同程度的影响,在相同的外荷载条件下,压力盒对上述因素都很敏感。因此,外界因素和新研究方法的组合考虑才能获得更为准确的土压力盒系数,才能运用于工程实践进行有效监测。
综上所述,实测过程中,由于压力盒自身材料的影响,其测值会有明显的迟滞性,颗粒特性不同其对应的迟滞性不同,形成的力-应变曲线也不同,那么对应的监测值也会不同。因此,对不同实际工程进行测试时,对岩土体力学参数进行实地勘测并进行理论分析,然后选择合适的土压力盒,以此指导实际工程设计和施工。
[1]Naoki F,Takehiko M,Kazuko K N,et al.Fabrication and efficiency evaluation of a hybrid Ni Cr Ai pressure cell up to 4Gpa[J].American Institute of Physics:Review of Scientific Instr u ments,2007,78(7):739-743.
[2]陈春红,刘素锦,王钊.土压力盒的标定[J].中国农村水利水电,2007(2):29-33.CHEN Chunhong,LIU Sujin,WANG Zhao.Calibration of earth pressure cell[J].China Rural water and Hydropower,2007(2):29-33.
[3]李贯军,王玉洁.监测设计中如何选择性能优良的压力盒[J].大坝与安全,2005(6):4-6.LI Guanjun,WANG Yujie.How to select pressure cell during monitoring design[J].Dam and Safety,2005(6):4-6.
[4]Theroux B,Labuz J F,Dai Shongtao.Field installation of an eart h pressure cell[J].Transportation Research Recor d,2001,1772:12-19.
[5]Joseph F L,Brent T.Laboratory calibration of earth pressure cells[J].Geotechnical Testing,2005,28(2):188-196.
[6]Zhu B,Jardine R.The use of miniature soil stress measuring cells in laboratory applications involving stress reversals[J].Soils and Foundations,2009,49(5):675-688.
[7]王涛,吕庆.颗粒离散元方法中接触模型的开发[J].岩石力学与工程学报,2009,28(Sup2):4040-4045.WANG Tao,LYU Qing.Developement of confalt model in particle discrete,element met hod[J].Chinese Jour nal of Rock Mechanics and Engineering,2009,28(Sup2):4040-4045.
[8]Chareyre B,Villard P.Dynamic spar elements and discrete element methods in t wo dimensions f or the modeling of soil-inclusion problems [J].Jour nal of Engineering Mechanics,2005,131(7):689-698.
[9]Jiang M J,Yu H S,Harris D.Discrete element modelling of deep penetration in granular soils[J].Int J Numer Anal Methods Geomech,2005,30:335-361.
[10]Orianne J,Daniel D,Richard K.Discrete element modelling of a granular platfor m supported by piles in soft soil-Validation on a s mall scale model test and co mparison to a nu merical analysis in a continuu m[J].Computers and Geotechnics,2009,36:917-927.
[11]Zhou C, Jin Y O.Nu merical investigation of progressive develop ment of granular pile with spherical and non-spherical particle[J].Mechanics of Materials,2009,41:707-714.
[12]Pradip R,Alexander S.Si mulation study on micr o and macro mechanical behaviour of sand piles[J].Powder Technology,2010,204:113-123.
[13]李凡.岩土材料破损特性的颗粒流研究[J].土木工程学报,2007,40(9):78-81.LI Fan.A study on the breakage properties of geological materials using particle flow si mulation[J].China Journal of Civil Engineering,2007,40(9):78-81.
[14]Manual of Particle Flow Code in 2 Di mensions:Theory and background[M].Itasca Consulting Group,Inc,2008.
[15]孙其诚,王光谦.颗粒物质力学导论[M].北京:科学出版社,2009.
[16]常在,杨军,程晓辉.砂土强度和剪胀性的颗粒力学分析[J].工程力学,2010,27(4):95-104.CHANG Zai,YANG Jun,CHENG Xiaohui.Granular mechanical analysis of the strength and dilatancy of sand[J].Engineering Mechanic,2010,27(4):95-104.
[17]许江,杨秀.周期性载荷作用下岩石滞回曲线的演化规律[J].西南交通大学学报,2005,40(6):754-758.XU Jiang,YANG Xiu.Evolution law of hysteresis curve of rock under cyclic loading [J].Jour nal of Southwest Transport University,2005,40(6):754-758.
[18]席道瑛,陈运平.岩石的非线性弹性滞后特征[J].岩石力学与工程学报,2006,25(6):1086-1093.Xi Daoying,Chen Yunping.Nonliear elastical hysteric characteristics of rocks[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(6):1086-1093.
