破舱进水对船舶横摇运动的影响

黄衍顺，汪娟娟，王珊珊

破舱进水对船舶横摇运动的影响

黄衍顺，汪娟娟，王珊珊

(天津大学建筑工程学院，天津 300072)

为研究船舱破损进水对船舶横摇运动的影响，建立了破舱进水船舶在规则横浪中的横摇运动微分方程，将进舱水晃荡产生的动力矩作为作用于船舶的外力矩．利用FLOW-3D对进舱水产生的动力矩进行仿真模拟计算，利用Matlab编程对破舱进水的横摇运动方程求解，计算分析破舱进水晃荡对船舶横摇运动的影响．以一艘拖轮为例，用时域法对不同波浪频率下的横摇运动响应进行计算，对比分析了规则横浪中的完整和破舱状态船舶的横摇运动响应特性．结果表明，在船舶大幅运动时，进舱水液面会成波浪状，产生翻卷和破碎，引起较大的合外力矩，使横摇运动幅值增大，危及船舶安全．

船舶破损；破舱稳性；进舱水；晃荡；动力矩

关于船舶破舱进水的动力作用对船舶运动影响的研究，目前还没有见到非常成熟的成果．许多学者对这一课题进行了认真研究，夏利清等[1]在论文中提到根据频域下的线性势流理论对船舶运动与舱内水晃荡之间的耦合作用进行研究，Santos等[2]利用浅水理论和随机选择法在时域方法下对进舱水的运动进行了模拟，得出了在一定的高频波浪作用下，进舱水对船体的动力矩是静力矩的3倍的结论．计算机和计算流体力学的发展，为进舱水运动的数值计算提供了可靠的硬件条件和理论基础，从而使得进舱水晃荡对船舶横摇运动的影响问题得到了圆满解决．

笔者将进舱水晃荡产生的动力矩作为作用于船舶的外力矩，利用FLOW-3D对进舱水产生的动力矩进行仿真模拟计算，利用Matlab编程求解破舱进水的横摇运动方程，计算分析破舱进水晃荡对船舶横摇运动的影响．

1 理论分析与计算方法

1.1 船舶运动坐标系

采用常规的3个坐标系来描述空间点、海浪和船体运动的关系[3]，即空间固定坐标系O1ξηζ、动坐标系Gxbybzb和随船平移坐标系Oxyz，3个坐标系都采用了垂直轴沿铅垂线向上的右手定则，如图1所示.

1.2 横摇运动微分方程

不考虑运动的耦合作用，完整船舶在规则横浪中的横摇运动方程[3]为

式中：Ixx为船舶横摇质量转动惯量，kg· m2；ΔIxx为船舶横摇附加水质量转动惯量，kg· m2；B为船舶横摇阻尼力矩系数；C为恢复力矩系数；F˜为波浪主扰动力矩，kg· m．

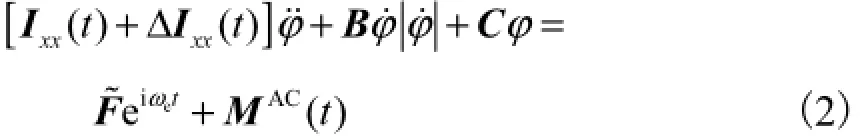
考虑非线性平方阻尼及进舱水晃荡产生的动力影响的破舱进水船舶在规则横浪中的横摇运动方程为式中：MAC(t)为进舱水晃荡对船舶重心的横摇力矩，kg· m；Ixx(t)为随时间变化的船舶横摇质量转动惯量，kg· m2；ΔIxx(t)为随时间变化的船舶横摇附加水质量转动惯量，kg· m2；ωe为遭遇频率，Hz．

1.3 船舶破舱进水计算

假定船舶的某舱一舷破损进水并对称发展，不考虑船舱复杂结构以及渗透率对进水影响的简化条件下，船舶进水后不会产生横倾，但会产生新的纵倾．新的船舶重心纵向、垂向坐标可根据破舱进水量和舱室位置进行计算．

实际海况中船舶的进水量是一个复杂的随时间变化的过程，本文简化如下：在船舶破损状态下，假设初始进水率为A，随着船体下沉，进水率不断变化．设进水率以α变化，则若以开始进水时刻为计时零点，进水后船舶的质量[4]可以表示为

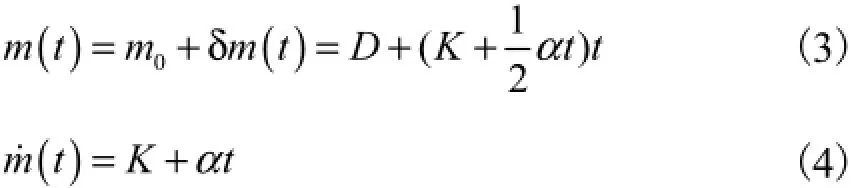
式中：0m为未进水时完整状态下船舶的排水量，即通常的船舶排水量D，kg；()m tδ为船舶随时间变化的进水量，kg．

对破舱后的进水采取增加重量法处理，则随时间变化的船舶横摇质量转动惯量和船舶重心位置为

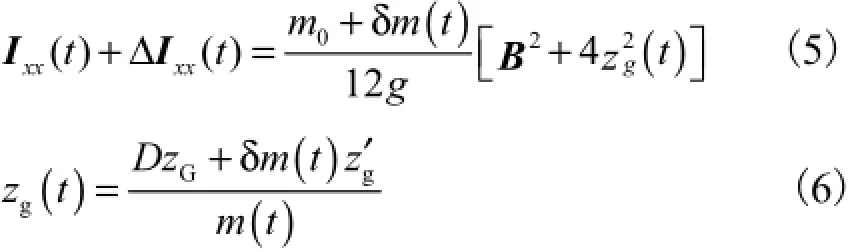
式中：zg为船体随时间变化的重心距基线高度，m；zG为初始进水时刻船体重心在基线以上的高度，m；zg′为进舱水随时间变化的重心高度，m，在特定时刻，它与破舱的形状与位置相关．此外在破舱情况下，初稳性高度、横摇周期Tφ也会随时间发生变化，其中

除了固定不变的参数，(Ixx+ΔIxx)仅与破舱因素以及船舶进水量相关．可根据破舱的舱容曲线将进舱水的重心高度转化为进水量的函数，由于进水量又是时间的函数，因此可以得出进舱水的重心高度随时间变化的函数表达式，最终求出(Ixx+ΔIxx)与进水时间之间的函数关系．

1.4 船舶横摇运动微分方程求解

破舱进水船舶在规则横浪中的横摇运动方程(2)中，[Ixx(t)+ΔIxx(t)]由式(5)和式(6)计算求解；船舶横摇阻尼力矩系数B由平方阻尼系数的渡边公式[5]求解，即

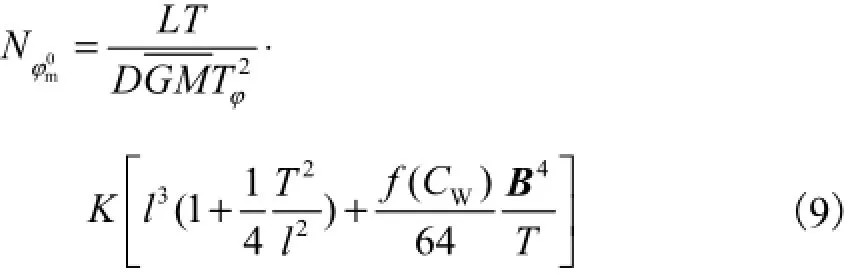
式中：Nφ0为阻尼力系数；L为垂线间长，m；T为吃

m水，m；K为考虑了船型、主尺度及舭龙骨影响的系数；l为横摇惯性矩，

对破舱内流体晃荡模型，利用VOF法对自由液面进行追踪模拟计算[8-9]；对考虑进舱水晃荡水动力矩影响的船舶横摇运动方程[10]，利用Matlab编程求解.

2 实例计算与结果分析

在上述理论计算的基础上，运用FLOW-3D计算流体力学软件和Matlab编程，对一艘拖轮进行实例计算分析．

2.1 船舶基本参数

船舶基本参数如表1所示．

表1 船舶基本参数Tab.1 Basic parameters of the ship

假设破损的舱室在61号肋位与77号肋位间，破口位于距船中11.3～12.7,m之间，破损位置垂向高度位于距基线2.2～2.6,m之间，进水沿船宽对称发展．

破舱具体参数见表2．

表2 破舱数据Tab.2 Data of broken cabin

2.2 波浪载荷参数

实例计算中，波浪幅值1.2,m，计算对比了4个波频下船的横摇运动，各波频下波浪力矩的幅值见表3．

表3 各波频下波浪力矩幅值Tab.3 Wave force moment amplitude of each wave frequency

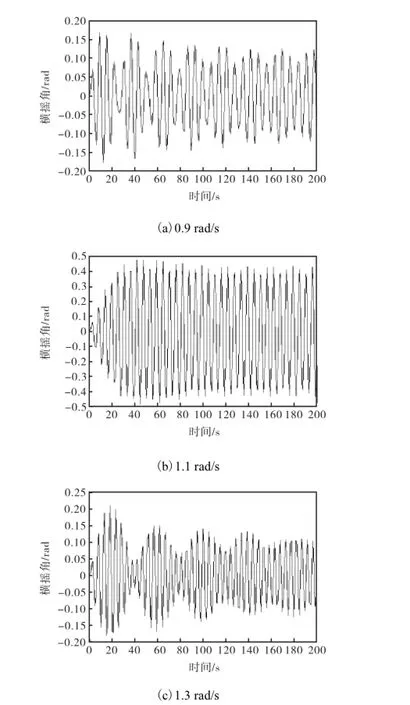
图2 不同波浪频率下船舶横摇角Fig.2 Ship’s roll angles under different wave frequencies

2.3 模拟计算结果与分析

2.3.1 不同波浪频率下完整船舶的横摇角

分别取波频激励为0.9,rad/s、1.1,rad/s和1.3,rad/s，则船舶横摇角计算结果如图2所示．

从图2中可看出，0.9,rad/s和1.3,rad/s状态的船舶的横摇幅值，都比1.1,rad/s状态的横摇幅值小，这是因为本船的横摇固有频率为1.14,rad/s，此时处在接近横摇共振状态．

2.3.2 完整状态与破舱进水船舶横摇运动对比

首先对破舱进水过程中的前26.83,s(在此过程中，外界海水不断涌入船舱)的船舶横摇运动进行数值求解(将进舱水作为移入舱内的静态载荷)，然后与完整状态下的船舶横摇运动进行对比分析．进舱水对横摇运动的影响，体现在船舶质量转动惯量和附加水质量转动惯量之和随时间的变化以及对初稳性高度的影响上．计算结果如图3所示．

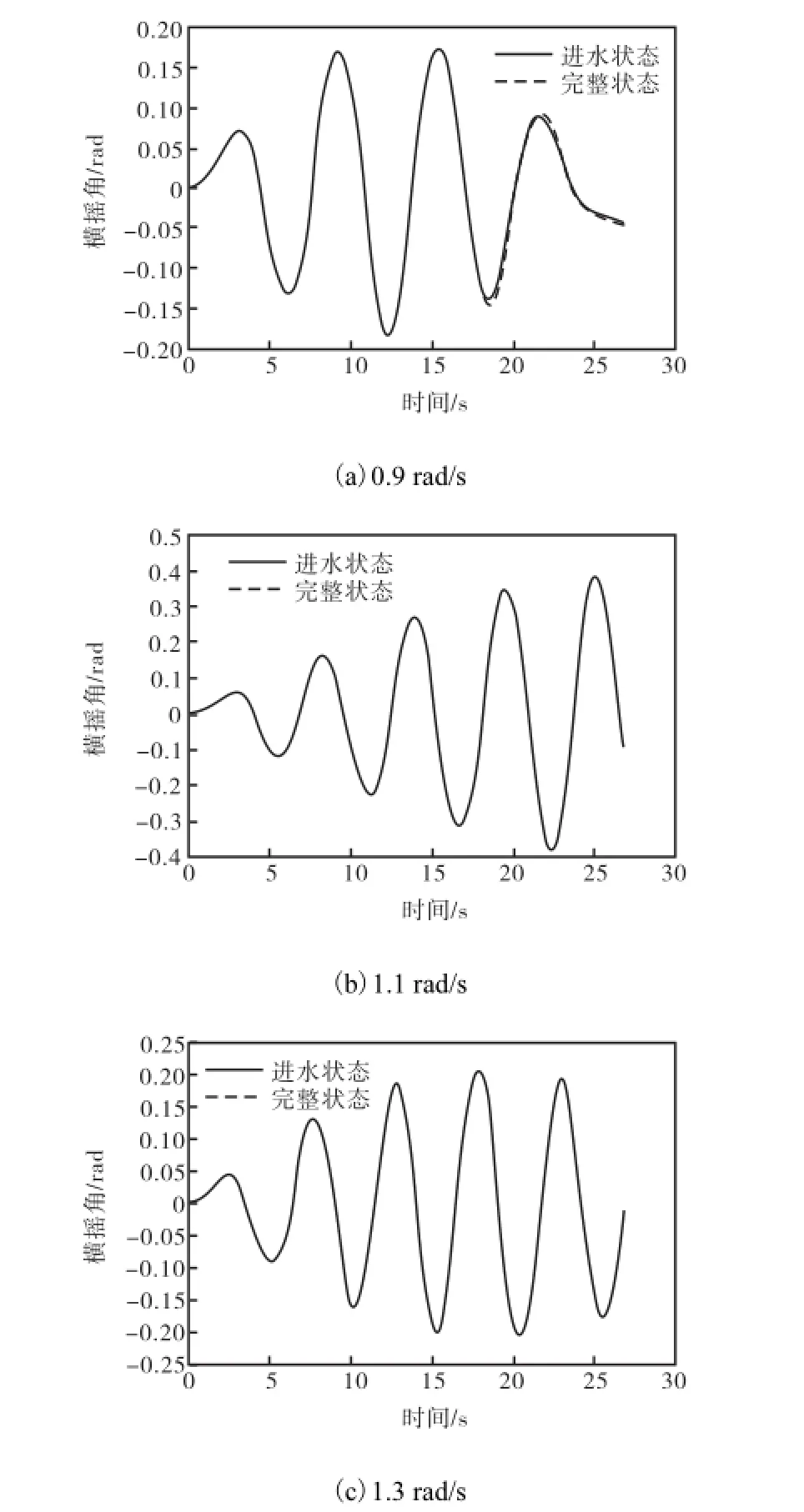
图3 不同波浪频率下横摇角对比Fig.3 Roll angle contrast charts under different wave frequencies

在船舶进水初期，进水量很小，破损舱室位于船舶底端，使得船舶重心降低，由式(5)和式(7)可知，船舶质量转动惯量与附连水质量转动惯量之和发生变化，船舶初稳性高度增大．而由于破损舱室靠近船体基线，进舱水重量与船舶排水量相比是小量，故破损引起的横摇角变化不大．还可看出，随着波浪频率的提高，船舶横摇周期减小，横摇频率增大，横摇幅值增大．

从图3可以看出，如果将进舱水仅仅看作是移入舱内的静态载荷，则进舱水对船舶运动的影响很小．但实际情况并非如此，因此在破舱状态下，需要考虑进舱水对横摇的动力影响．

2.3.3 船舶横摇对舱内水运动的影响

随着时间的推移，船舶运动对进舱水运动产生的影响如图4所示．

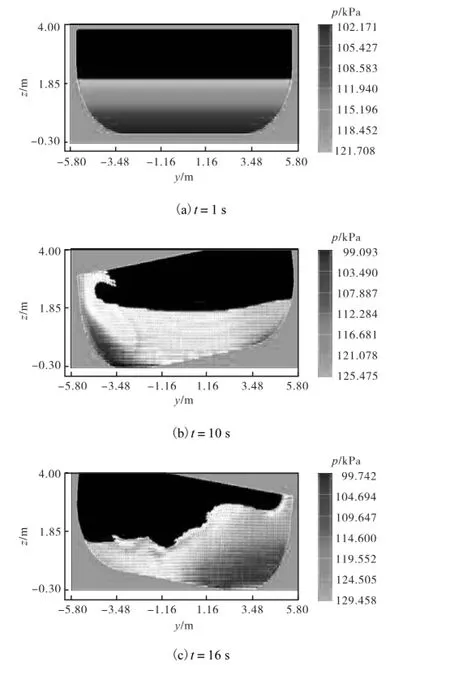
图4 0.9,rad/s时船舶运动对进舱水运动的影响Fig.4 Influence of the roll motion acting on the floodwater under the wave frequency of 0.9,rad/s

从图4中可以看出，在船舶刚开始运动时，横摇角较小，进舱水液面近似为水平；但在较大横摇角下，进舱水会产生严重的晃荡，翻卷和破碎，对船舶稳性及强度产生很大影响，其动力作用不可忽视．

2.3.4 进舱水动力矩对船舶横摇运动的影响分析

1)不同波浪频率激励下进舱水动力矩

不同波浪频率激励下进舱水动力矩如图5所示.

从图5中可以看出进舱水动力矩近似正弦规律变化，其幅值大小与波浪频率密切相关．在共振频率1.14,rad/s之前，随着波浪频率的增加，进舱水动力矩幅值随之增大，非线性增强．波浪频率为1.3,rad/s时的水动力矩幅值要小于0.9,rad/s，说明0.9,rad/s的波浪激励更接近船舶的共振频率．

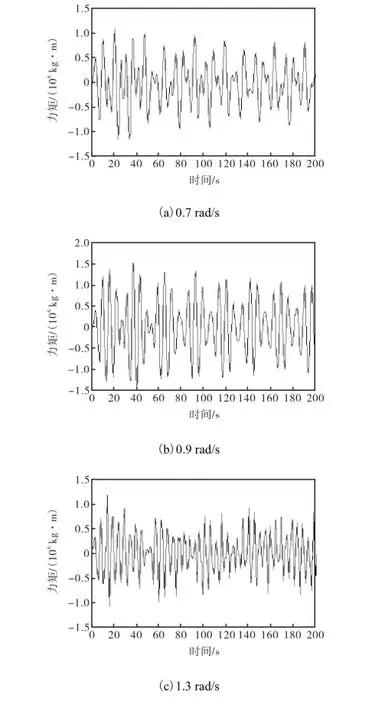
图5 不同波浪频率下进舱水动力矩Fig.5 Dynamic roll moments of floodwater under different wave frequencies

2)不同波浪频率下，波浪力矩、进舱水动力矩及二者合力矩

进舱水深度为2,m时，不同波浪频率下，波浪力矩、进舱水动力矩及二者合力矩如图6所示．

从图6中可看出进舱水晃荡运动十分显著，其产生的动力矩最大幅值与波浪力矩最大幅值相比不相上下；随着波浪激励频率的增加，水动力矩的最大幅值甚至超过了波浪力矩．从图中也可看出虽然进舱水动力矩与波浪力矩之间会存在一定的相位差，但产生的合力矩比进舱水动力矩以及波浪力矩都要大．

合力矩总体上是稳定的，类似正弦规律变化；随着波浪激励频率的增加，进舱水动力矩、合力矩的幅值都随之增加，频率增大．

图6 不同波浪频率下3个力矩对比Fig.6 Three moments’ contrast chart under different wave frequencies

2.3.5 不同波浪频率下船舶的横摇角

在考虑了进舱水动力矩对船舶横摇运动作用下，利用Matlab编程求得破损船舶在不同波浪激励频率下的横摇角，计算结果如图7所示．

与图3相比，可以看出考虑了进舱水动力矩后，在不同的波浪激励频率下船舶的横摇幅值均有大幅度的增大，这对船舶的稳性很不利，由此可知考虑进舱水动力矩的重要性及必要性．从图中还可看出0.9,rad/s波浪激励下的横摇角幅值要高于其他频率，这意味着0.9,rad/s更接近船舶破损后的共振频率，由此可知由于进舱水动力矩的影响使得共振频率发生变化．

图7 不同波浪频率下破损船舶横摇角Fig.7 Damaged ship’s roll angles under different wave frequencies

3 进舱水动力矩的敏度分析

3.1 不同深度的进舱水产生的动力矩

假设破损的舱室依然发生在61号肋位与77号肋位之间，讨论进水深度分别为0.5,m、1.0,m、1.5,m和2.0,m的进舱水产生的动力矩．

由于篇幅限制，只选择了波浪激励频率为0.9,rad/s下的水动力力矩对比，如图8所示．

从图8中可以看出，随着进舱水水深的增加，所产生的水动力矩逐渐增大．但增加的幅度有所不同．当进舱水深度为1.0,m时，其产生的水动力矩要远大于0.5,m进舱水产生的水动力矩．而当进舱水深度为2.0,m时，其产生的水动力矩与1.5,m进舱水产生的水动力矩差值较前者较小．此外，在进水深度较小(0.5,m)时，进舱水动力矩呈现衰减的趋势．

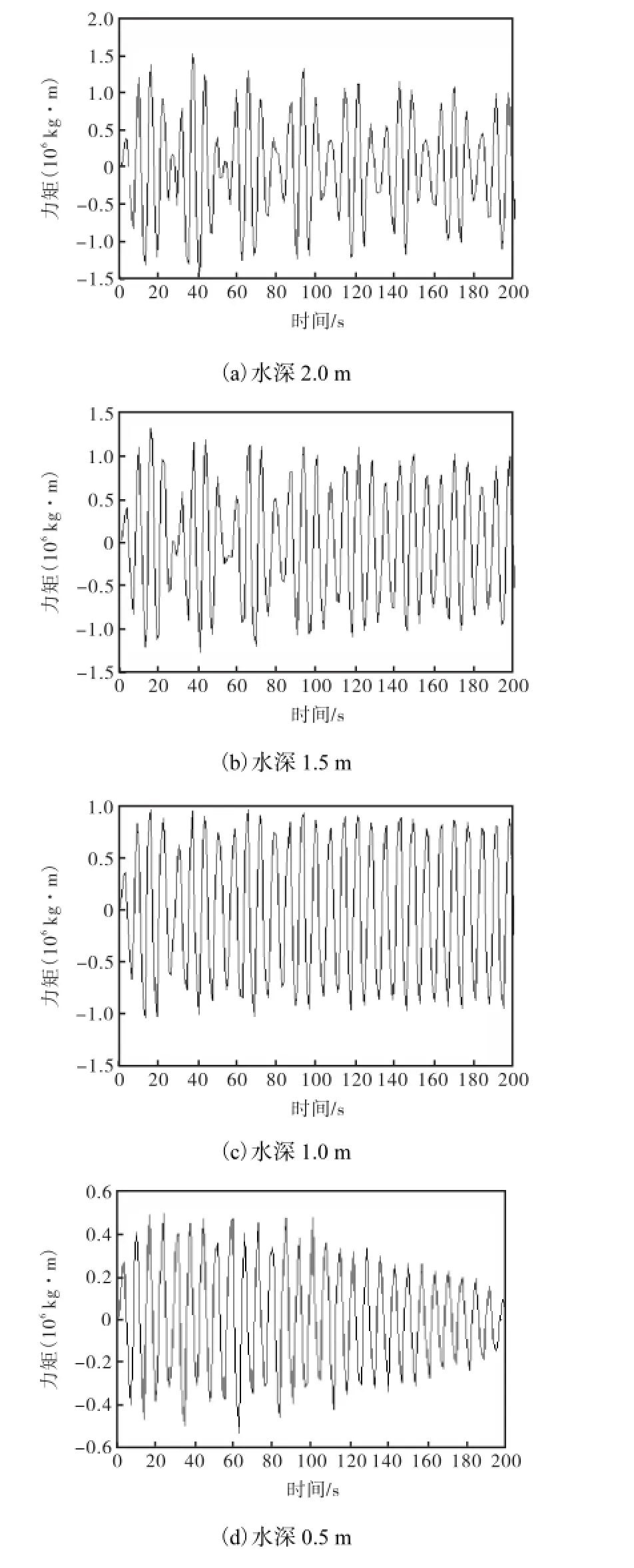
图8 0.9 rad/s不同水深的进舱水动力矩Fig.8 Dynamic roll moments of floodwater at different depths

3.2 对称与非对称进舱水产生的动力矩

假设破损的舱室依然发生在61号肋位与77号肋位之间，分别讨论舱室形状为对称与非对称时进舱水所产生的动力矩．假设进水深度均为2.0,m，波浪激励频率为0.9,rad/s．

从图9和图10中可以看出，对称与非对称进舱水所产生的动力矩变化趋势有所不同．对称进水时，其产生的动力矩呈类似正弦规律变化，而非对称进水时，产生的动力矩总体上是稳定的，只有在最开始的时间内呈现出较大的幅值．此外，对称进舱水所产生的动力矩总体上大于非对称进舱水产生的动力矩，这一结果与实际工程相符．

图9 非对称进舱水动力矩Fig.9 Dynamic roll moment of asymmetric floodwater

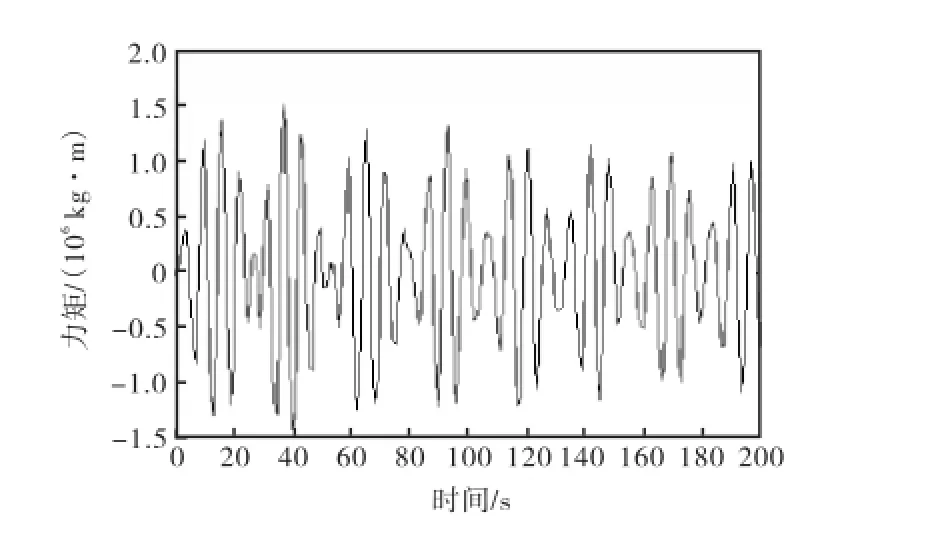
图10 对称进舱水动力矩Fig.10 Dynamic roll moment of symmetric floodwater

3.3 不同破舱位置进舱水产生的动力矩

3.3.1 破损舱室数据

以波频激励为0.9,rad/s、进水深度2.0,m为例，分析破损分别发生在40号～50号肋位、50号～61号肋位以及61号～77号肋位时，进舱水动力矩的变化情况．破损舱室位置见表4．破损舱室结构见图11.

表4 破损舱室位置Tab.4 Position of damaged cabin

图11 破损舱室结构Fig.11 Structure of damaged cabin

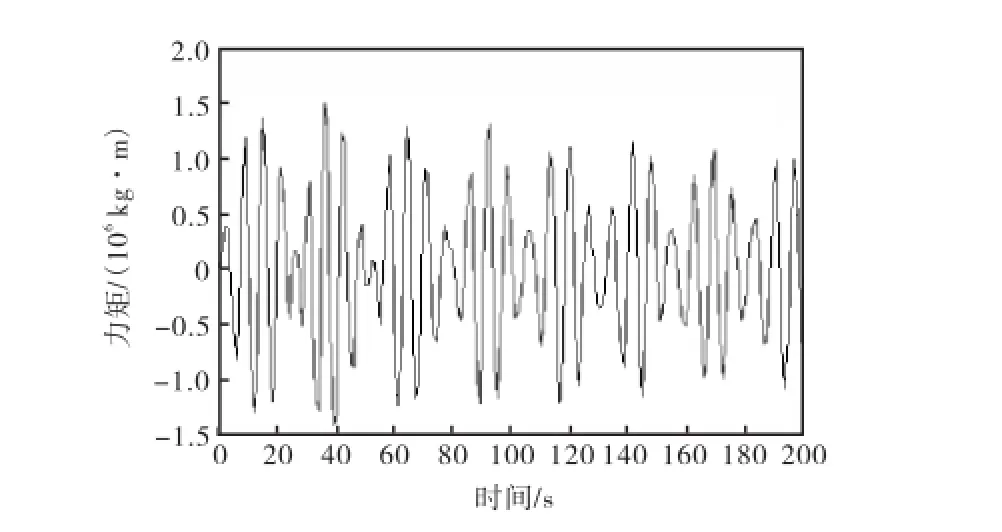
图12 60号～77号进舱水动力矩随时间的变化曲线Fig.12 Dynamic roll moment of floodwater vs time (No.60—No.77)

3.3.2 计算结果分析

不同位置进舱水动力矩随时间的变化情况如图12～图14所示．

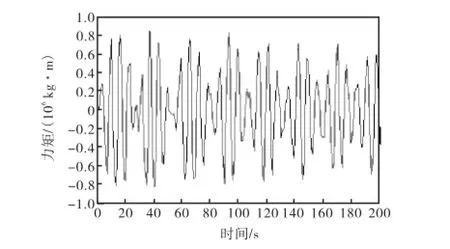
图13 50号～61号进舱水动力矩随时间的变化曲线Fig.13 Dynamic roll moment of floodwater vs time (No.50—No.61)

图14 40号～50号进舱水动力矩随时间的变化曲线Fig.14 Dynamic roll moment of floodwater vs time (No.40—No.50)

从图12～图14中可以看出，不同位置的进舱水所产生的动力矩变化趋势大致相同，类似正弦规律变化．但所产生的动力矩数值差别较大，距离船中越远，进舱水所产生的动力矩越大．而在40号～50号处进舱水产生的动力矩较小，原因在于舱室破损的位置大概发生在船中处，舱室中心与船中接近．

4 结 论

本文将进舱水晃荡产生的动力矩作为作用于船舶的外力矩，利用FLOW-3D对进舱水产生的动力矩进行仿真模拟计算，利用Matlab编程求解破舱进水的横摇运动方程，计算分析破舱进水晃荡对船舶横摇运动的影响，经实船计算分析可得如下结论．

(1) 进舱水动力矩对船舶横摇运动幅值影响较大，进舱水对船舶产生的动力矩与波浪力矩之间存在一定的相位差，引起了比二者都大的合力矩，对船舶稳性很不利，在实际工程计算中考虑进舱水动力矩是非常必要的．

(2) 由于进舱水动力矩的影响，共振频率发生变化，有向低频移动的趋势，本文实例中，共振频率由1.1,rad/s附近减小到0.9,rad/s附近．

(3) 从敏度分析可以看出，随着破舱进水深度的增加，进舱水所产生的动力矩随之增大，但增大的幅度逐渐变缓；对称与非对称破舱进水产生的动力矩都不容忽视，且其产生的动力矩呈现不同的变化趋势；破损舱室距离船中的距离越远，进舱水产生的动力矩越大，如果破损位置发生在船中附近，则其进舱水产生的动力矩很小．

［1］ 夏利清，范佘明. 船舶在波浪中破舱稳性数值计算方法综述[C]//船舶水动力学学术会议. 中国，武汉，2004：182-184. Xia Liqing，Fan Sheming. Ships in waves breaking cabin stability of the numerical calculation method[C]// Ship Dynamics Conference. Wuhan，China，2004：182-184(in Chinese).

［2］ Santos T A，Soares C G. Study of damaged ship motions taking into account floodwater dynamics[J]. Marine Science Technology，2008，13(3)：291- 307.

［3］ 李积德. 船舶耐波性[M]. 哈尔滨：哈尔滨工程大学出版社，1992. Li Jide. Ship Resistance[M]. Harbin：Wave of Harbin Engineering University Press，1992(in Chinese).

［4］ 郭显杰. 规则斜浪中破损船舶进水后的运动响应研究[D]. 天津：天津大学建筑工程学院，2006. Guo Xianjie. Research on the Motion Response of Damaged Ship on Regular Oblique Waves[D]. Tianjin：School of Civil Engineering，Tianjin University，2006(in Chinese).

［5］ 元良诚三. 船舶与海洋构造物动力学[M]. 天津：天津大学出版社，1992. Yuanliang Chengsan. Ship and Marine Installations Dynamics[M]. Tianjin：Tianjin University Press，1992(in Chinese).

［6］ Barkhudarov M R. Lagrangian VOF Advection Method for Flow-3D[EB/OL]. http://www.flow3d.com/pdfs/tn/ FloSci-Tn63R.pdf，2004-07.

［7］ Yao G F. Development of New Pressure-Velocity Solvers in Flow-3D[EB/OL]. http://www.flow3d.com/pdfs/tn/ FloSci-Tn63R.pdf，2004-04-20.

［8］ 王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京：清华大学出版社，2004. Wang Fujun. Computational Fluid Dynamics Analysis—CFD Software Principle and Application[M]. Beijing：Tsinghua University Press，2004(in Chinese).

［9］ 朱仁庆. 液体晃荡及其与结构的相互作用[D]．无锡：中国船舶科学研究中心，2001. Zhu Renqing. Liquid Flap About and Structure of Interaction[D]. Wuxi：China Ship Scientific Research Centre，2001(in Chinese).

［10］ 郜焕秋，谢 楠. 舱内水体晃荡对船舶横摇影响的模型试验研究[J]. 船舶力学，1998，2(6)：1-14. Gao Huanqiu，Xie Nan. Experimental study on effect of sloshing on ship roll motion[J]. Ship Mechanics，1998，2(6)：1-14(in Chinese).

Effects of Floodwater on the Roll Motion Response of Broken Ships

HUANG Yan-shun，WANG Juan-juan，WANG Shan-shan
(School of Civil Engineering，Tianjin University，Tianjin 300072，China)

In order to investigate the effects of floodwater on the roll motion response of broken ships，the rolling differential equations of a damages ship in regular beam waves were established. Floodwater’s sloshing produced a dynamic roll moment and this moment was considered to be the moment acting on the ship. FLOW-3D was used to simulate calculation of the dynamic roll moment produced by floodwater，and Matlab was used to solve the roll motion equation. Then the influence of the floodwater acting on the roll motion was calculated and analyzed. With a tug as an example，the different wave frequencies of roll motion response were calculated by use of time domain method and then the differences of rolling movement response characteristics between intact ship and damaged one in regular waves were analyzed. The results show that，when ship moves with large margin，liquid surface of floodwater will become wavy，producing rolling and breaking，and cause a larger total moment，so that the roll motion amplitude increases and the safety of the ship is endangered.

shipbreaking；damaged stability；floodwater；sloshing；dynamic roll moment

U661.23

A

0493-2137(2012)07-0577-08

2011-02-28；

2011-09-09.

黄衍顺（1946— ），男，教授.

黄衍顺，hysh4637@yahoo.com.cn.