传统断裂力学参量在TBCs界面断裂中的可行性分析

荆洪阳，杨 祯，徐连勇，刘发安

传统断裂力学参量在TBCs界面断裂中的可行性分析

荆洪阳1,2，杨 祯1，徐连勇1,2，刘发安3

(1. 天津大学材料科学与工程学院，天津 300072；2. 天津市现代连接技术重点实验室，天津 300072；3. 中国石油集团工程设计有限责任公司华北分公司，任丘 062552)

通过对TBCs/Q345涂层试样进行拉伸强度测试试验，并结合有限元模拟计算，对复应力强度因子K及J积分用于评定TBCs涂层界面断裂问题的可行性进行了分析．通过采用应力计算法计算涂层界面裂纹的复应力强度因子K，发现在裂纹尖端区域存在一个K主导的弹性区域，可以说明K因子有效，可用于评价脆性涂层的界面断裂问题；而通过有限元方法得到的J积分分布很不均匀，表明J积分不适于评价涂层的界面断裂问题．

涂层；断裂参量；界面裂纹；有限元分析

近年来，热障涂层技术在发动机涡轮叶片的设计中得到越来越广泛的应用，它对提高叶片的耐高温能力以及延长发动机的使用寿命起到了关键的作用．一般地，航空发动机涡轮叶片表面的热障涂层由Y2O3部分稳定的ZrO2(YSZ)陶瓷面层和MCrAlY金属黏接底层两部分组成．但对于多重涂层系统而言，不同涂层之间、涂层与基体的剥离，以及涂层内部开裂是导致整个热障涂层系统失效的主要形式；而提高涂层与基体的结合强度、保证涂层与基体的完整性是构件安全服役的关键．因此，研究热障涂层的断裂行为对于TBCs的失效具有指导意义[1-2]．笔者对采用电子束物理气相沉积(EB-PVD)技术制得的热障涂层的断裂行为进行了研究．通过制备TBCs/Q345涂层试样并对之进行力学试验，结合有限元模拟手段，介绍了应力计算法求解界面复应力强度因子的方法，并重点分析了传统的断裂力学参量(复应力强度因子K和J积分)对于描述界面断裂行为的有效性．

1 力学试验

该试验是根据ASTM C633—79[3]测试胶黏试样结合强度的拉伸试验测试标准，在改进试样的基础上进行的．改进的拉伸试样中，基体部分为高40,mm、半径12.7,mm的Q345圆柱，圆柱顶端面的中心热喷涂一层厚100,nm、半径为8,mm的碳膜，在碳膜的表面是采用电子束物理气相沉积方法制备的TBCs．之后，用环氧树脂Epoxy黏结剂将此部分与另外一段同样尺寸的Q345钢柱粘在一起[1](见图1)．这样，由于碳膜与基体圆柱之间几乎无结合力，在TBCs与基体之间的碳膜就充当了一个硬币状的预制裂纹．为保证试验精度，降低随机误差的影响，共制备8个试样进行试验．表1为试样陶瓷层的化学成分．

图1 改进的拉伸试样示意Fig.1 Schematic diagram of revised tensile specimen

表1 YSZ陶瓷层的化学成分Tab.1 Constitution of ceramic top coats %

室温静载的拉伸试验在CSS-44100万能材料试验机上进行，试验过程中记录下施力点的位移-载荷曲线．表2列出了8个试样发生断裂时的临界载荷Pc．由表2可知，8个试样的临界断裂载荷分布不均匀，其原因是试样制备过程中有一些不可控因素如碳膜厚度、直径的精确控制等．

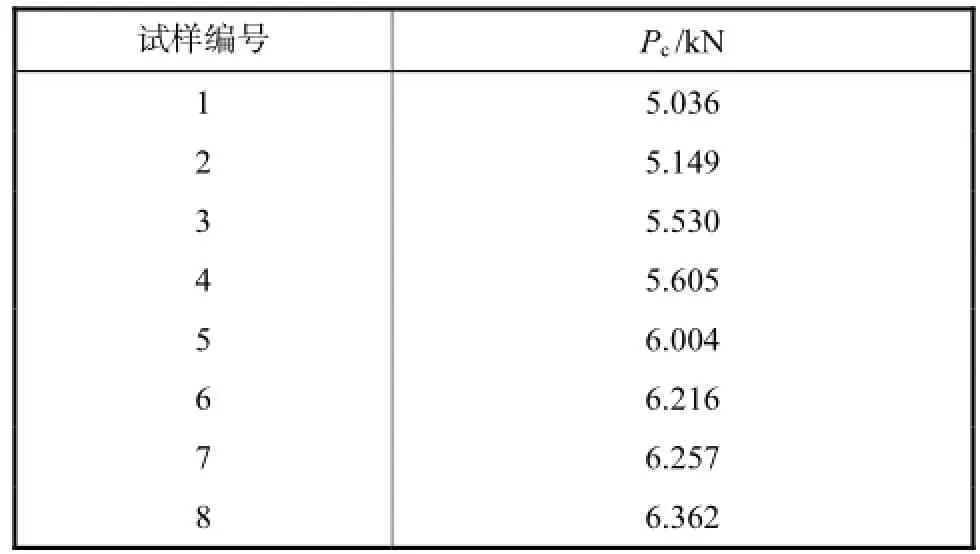
表2 拉伸试样界面发生断裂时的临界载荷Tab.2 Critical load of tensile specimens on interface crack initiation

2 应力计算法求解复应力强度因子

在涂层试样受载时，由于强度的不匹配，裂纹尖端区域往往不会单纯存在一种型式的应力场，而是以混合形式的奇异应力场存在，即裂纹尖端同时存在拉伸(Ⅰ型)和剪切(Ⅱ型)的复合应力场，它们分别对应不同的裂纹张开或滑移程度．两种应力场的比例直接影响涂层的破坏形式和裂纹能量释放率，因此在裂纹启裂时，将Ⅰ型裂纹和Ⅱ型裂纹的临界应力强度因子的比值称为相位角．通过研究相位角，可以得到特定类型涂层试样的裂纹临界能量释放率[4]．

刘刘等[5]研究了双层的热障涂层试样裂纹尖端复应力强度因子的计算方法，讨论了利用裂纹面上的位移数据和采用J积分来计算TBCs界面K因子的方法，两种方法的计算结果较为一致．其中，位移数据法较为简单，不但可以通过结合有限元数值模拟方法计算得到因子K，也可以通过试验手段得到相应的位移数据，但计算量大且不精确；J积分法计算因子K最为简单却不能同时计算相位角．

根据Rice[6]对界面裂纹复应力强度因子的定义，复应力强度因子K由KⅠ和KⅡ组成．有限元数值计算得到界面区域的应力，通过相关计算公式可以求解出K、相位角及2个分量(KⅠ和KⅡ)的值，这种计算界面裂纹复应力强度因子的方法即为应力计算法．Rice对双材料界面裂纹复应力强度因子K的定义为

式中：|K|为复应力强度因子K的模；β为相位角；i为虚数；KⅠ和KⅡ分别是Ⅰ型和Ⅱ型复应力强度因子．

图2中双材料界面裂纹尖端的应力分布表达式为

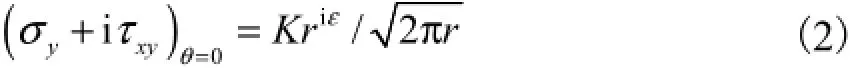
式中：σy为界面法线方向的应力；τxy为剪应力；r和θ均为极坐标参数；ε为界面的振荡系数，其定义为

图2 双材料界面裂纹尖端附近区域Fig.2 Region near crack tip along bi-material interface

这里，平面应变下，χ=3-4,ν，平面应力下χ= (3-ν)/(1+ν)，ν为泊松比；剪切模量μ=E/2(1+ ν)，E为弹性模量．

已知含裂纹均匀材料的复应力强度因子K的表达式为

根据式(2)，复应力强度因子的大小为

由欧拉公式

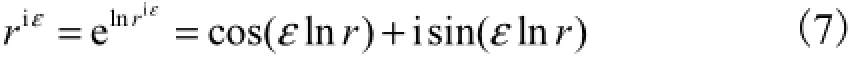
根据式(7)、式(2)和式(1)，得

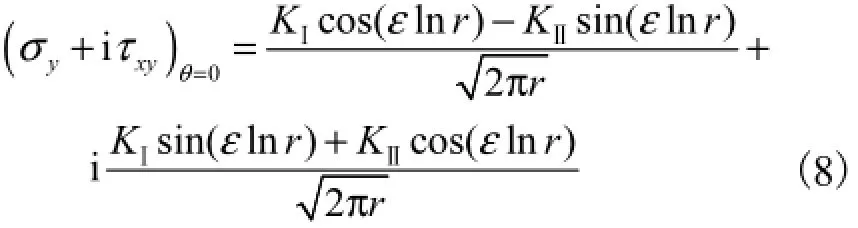
所以

根据式(9)和式(10)反解出KⅠ、KⅡ和相位角ψ分别为

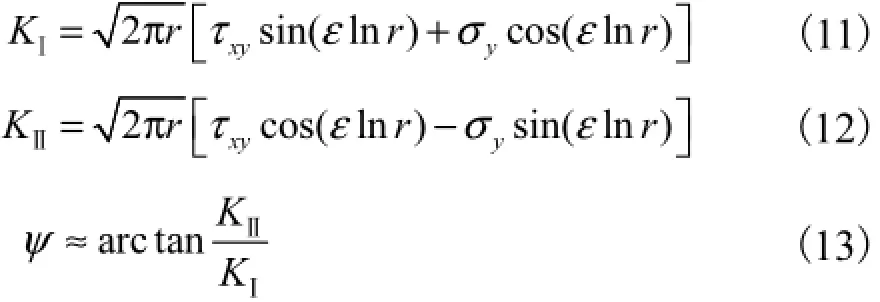
从有限元分析结果中提取出σy和τxy后，代入式(6)、式(9)～式(13)，即可求解出界面裂纹复应力强度因子K的模、KⅠ、KⅡ和相位角．

3 界面裂纹的传统断裂力学参量及其有效性分析

3.1 有限元分析

在第2节介绍的应力计算法中：有限元数值计算得到界面裂纹附近区域的应力，通过相关计算公式可算出K的模、相位角及2个分量(KⅠ和KⅡ)．所以，有限元分析是求解复合应力强度因子的关键步骤．

有限元计算所需要的Q345钢、金属黏结层、YSZ陶瓷面层和环氧树脂Epoxy的力学性能如表3和表4所示，其中表3所示为热障涂层中陶瓷面层、金属黏接底层以及Epoxy的弹性模量及泊松比，表4所示为Q345钢的力学参数．

因为圆柱试样的轴对称性，这里取试样的1/4模型建模．采用20节点等参六面体减缩积分单元．在界面裂纹尖端附近和界面两侧附近的区域网格划分精细，在远离界面和裂纹尖端的地方网格划分稀疏．由于涂层断裂是脆性断裂，所以此处不考虑塑性因素．图3所示为有限元模型和裂尖局部区域．

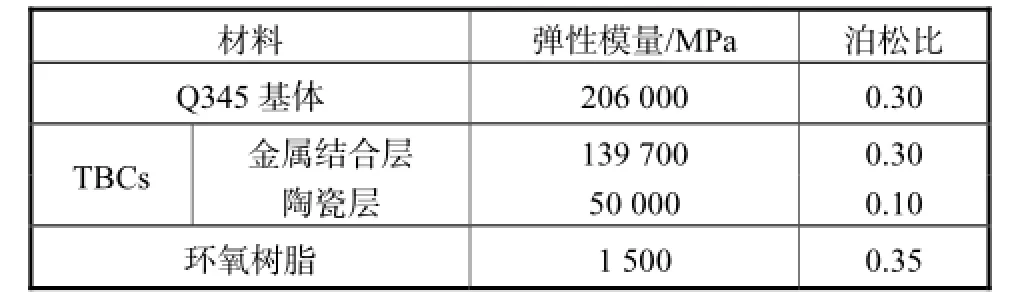
表3 涂层试样各部分的材料性能Tab.3 Material properties of the coating specimen

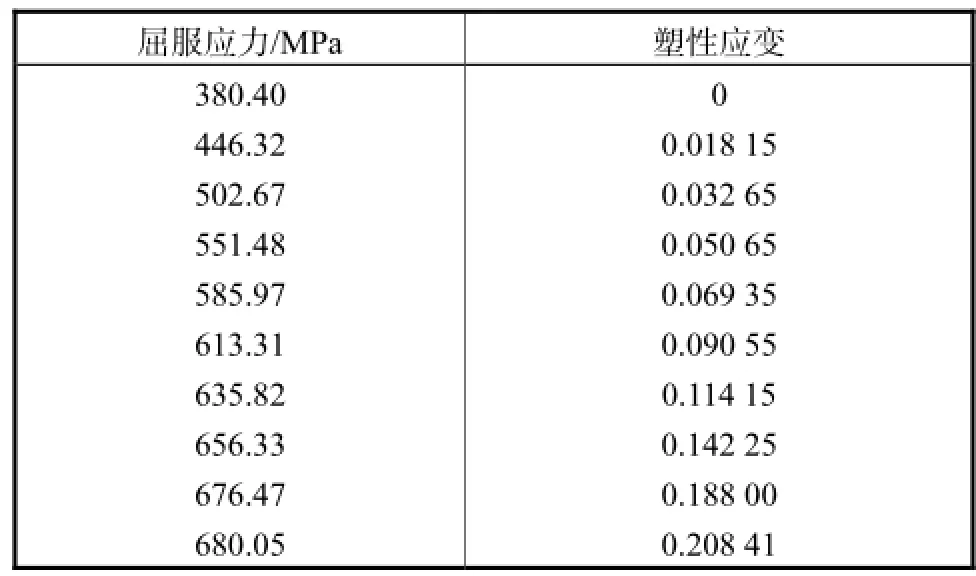
表4 Q345的力学性能Tab.4 Mechanics properties of Q345 steel

图3 有限元模型及裂尖区域Fig.3 Finite element model and crack-tip area

一般地，相位角表示了界面裂纹尖端剪切型和拉伸型复应力强度因子的相对大小．在2种极端情况下，ψ=0°和ψ=90°(或ψ=-90°)分别对应了剪切和拉伸载荷占主导的情形．

利用式(6)和式(11)～式(13)求解得到的10个载荷步下复应力强度因子的模|K|、KⅠ、KⅡ以及相位角ψ见表4．

从表4可以看出，Ⅰ型裂纹强度因子KⅠ远大于Ⅱ型裂纹强度因子KⅡ，且相位角ψ明显小于45°．这说明拉伸型载荷主导涂层界面裂纹尖端区域的断裂行为，并且拉伸效果要远大于剪切效果．

表4 各载荷步下复应力强度因子及其相位角Tab.4 Complex stress intensity factor and phase angle under each load step

3.2 界面裂纹复应力强度因子K的有效性分析

在含裂纹的均质材料中，如果裂纹尖端附近区域存在一个K因子主导的弹性区，则可以认为K因子对评定裂纹扩展行为是有效的[7]．根据式(6)和式(8)，涂层界面裂纹的复应力强度因子由裂纹面法线方向的正应力σy和平行于界面的剪应力τxy的平方和决定．所以可以通过二者沿裂纹面的分布大小来分析K因子的主导性．

根据式(3)得到ε=0.017,5．由此，再结合式(9)和式(10)，得

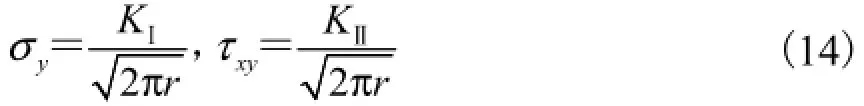
式中σy和τxy可直接由相应的KⅠ和KⅡ表示．这里为简化起见，取有限元分析过程中的5个载荷步来分析σy和τxy沿裂纹面的分布情况．图4给出了不同载荷水平下试样1涂层界面裂纹尖端附近的应力分布，1～5的载荷步代表了逐渐增大的载荷水平．从图4中可以看出，无论是哪个载荷水平下，σy的值都明显大于τxy，由此验证了表4的计算结果，Ⅰ型断裂是涂层发生失效的主要因素．其次，σy随着离裂纹尖端距离增大呈线性减小的趋势；而τxy在裂纹尖端很小范围内(≤0.08,mm)也是线性减小的．根据式(14)，可以认为界面的裂纹尖端存在一个K因子主导的弹性区，即K因子是有效的．

因此，结合有限元数值计算，采用应力计算法求解得到界面裂纹的复应力强度因子及其分量，可以定量分析裂纹尖端各个分量的控制因素．通过上述讨论得知，TBCs/Q345涂层试样的裂纹尖端存在K主导区，即K因子可以用来描述该类涂层系统的断裂行为．

图4 试样1涂层界面裂纹尖端附近的应力分布Fig.4 Distributions of normal stress and shear stress near the crack tip on the interface of specimen 1

3.3 热障涂层TBCs/Q345界面裂纹的J积分

众所周知，对于非线性材料而言，J积分是有效的断裂特征参量，而且，J积分还适用于弹性材料，此时J等价于能量释放率．

在有限元分析中，ABAQUS通过虚拟裂纹扩展原理[8-10]来计算J积分的值．表5给出了通过ABAQUS输出请求得到的8个试样的界面裂纹的临界J积分值(Jc)．由表5可以看出，8个试样的J积分值从0.088到0.140，相对来说变化较大．而按照断裂力学理论，传统的材料断裂力学控制参量如K、J和CTOD是材料的属性，即一个常数．对于热障涂层系统，不同涂层之间、涂层内部以及涂层与基体的界面上随机分布着很多微裂纹、孔洞、氧化物等微观缺陷，在构件承载时这些缺陷部位极易导致应力集中，削弱涂层与基体或涂层内部之间的结合强度．从这个角度上讲，由这些缺陷所引起的界面断裂也具有很大的随机性，试验得到的临界载荷和J积分也呈现明显的不均匀分布．所以，J积分不能作为评定热障涂层完整性的有效参量．

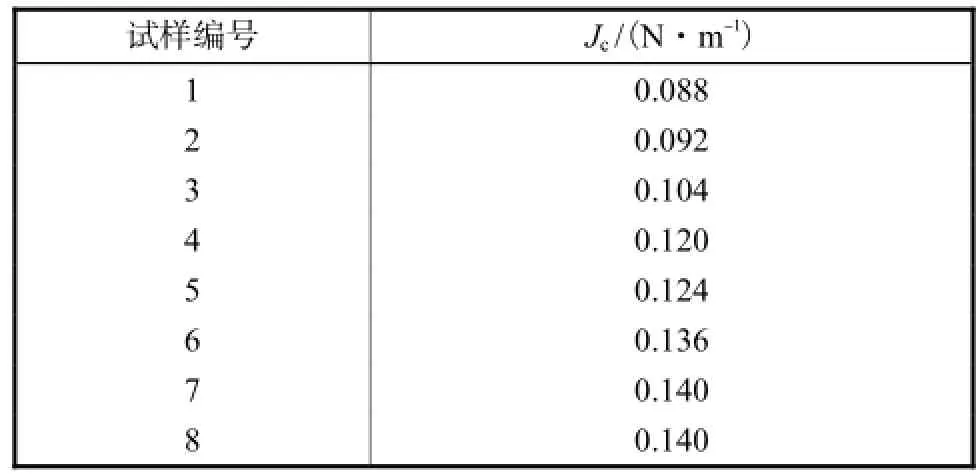
表5 有限元分析得到的裂纹尖端Jc值Tab.5 Jcintegral of interfacial crack tip determined by FEM

4 结 论

(1) 对于涂层界面的裂纹而言，与有限元方法相结合的应力计算法不但可以求解出界面裂纹的复应力强度因子及其分量，还能定量分析各个分量的控制因素，是一种比较实用有效的计算方法．

(2) 通过分析断裂力学参量对于描述TBCs/ Q345涂层系统界面断裂行为的适用性，发现界面裂纹的复应力强度因子K可以用来评价脆性涂层材料的界面断裂行为．而J积分呈现较大的分散性，不适于评价该类涂层的界面断裂问题．

［1］ Qian G，Nakamura T，Berndt C C，et al. Tensile toughness test and high temperature fracture analysis of thermal barrier coatings [J]. Acta Metallurgica，1997，45(4)：1767-1784．

［2］ Xu Lianyong，Jing Hongyang，He Ying. J-integral of interfacial crack between metal-base ceramic coating and steel [J]. Transactions of Tianjin University，2009，15(1)：32-36.

［3］ ASTM. C633—01 Standard Test method for Adhesion or Cohesive Strength of Thermal Spray Coatings[S]. West Conshohocken：ASTM International，2008.

［4］ Anderson T L. Fracture Mechanics：Fundamentals and Applications[M]. 2nd ed. Florida：CRC Press LLC，1995.

［5］ 刘 刘，杨晓光，耿 瑞. TBC界面裂纹K因子的有限元求解方法[J]. 航空动力学报，2000，15(2)：171-174. Liu Liu，Yang Xiaoguang，Geng Rui. The finite element method for solving K factor of TBC interfacial crack[J]. Journal of Aerospace Power，2000，15 (2)：171-174(in Chinese).

［6］ Rice J R. Elastic fracture mechanics concepts for interfacial cracks [J]. Journal of Applied Mechanics，1988，55(1)：98-103.

［7］ 徐连勇. 涂层/基体界面的断裂行为研究 [D]. 天津：天津大学材料学院，2006. Xu Lianyong. Reasearch on Fracture Behavior of Interface Between Coating and Substrate[D]. Tianjin：School of Materials Science and Engineering，Tianjin University，2006(in Chinese).

［8］ Parks D M. The virtual crack extension method for nonlinear material behaviour [J]. Computer Methods in Applied Mechanics and Engineering，1977，12(3)：353-364.

［9］ Hellen T K. On the method of virtual crack extensions [J]. International Journal for Numerical Methods in Engineering，1975，9(1)：187-196.

［10］ Nakamura T，Shih C F，Freund L B. Analysis of a dynamically loaded three-point-bend ductile fracture specimen [J]. Engineering Fracture Mechanics，1986，25(3)：323-339.

Feasibility Analysis of Traditional Fracture Mechanics Parameters for TBCs Interface Fracture

JING Hong-yang1,2，YANG Zhen1，XU Lian-yong1,2，LIU Fa-an3
(1. School of Materials Science and Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Advanced Joining Technology，Tianjin 300072，China；3. China Petroleum Engineering Company Limited North China Branch，Renqiu 062552，China)

Tensile tests were carried out to obtain the critical values when the interface crack initiation occurred between coatings and substrates. The finite element analysis(FEA)was adopted to analyze the stress distribution in the specimens and compute the complex stress intensity factor(K)and the J integral of the interface between TBCs and Q345,steel. The results indicate that a K-dominant elastic zone exists near the crack tip for all specimens，and K is an effective fracture parameter for interface fracture. In addition，the J integral values of all specimens are dispersive when the interface fracture occurs. Therefore，J integral is not appropriate to be used as the single fracture parameter to evaluate the interface fracture behavior.

coating；fracture parameter；interface crack；finite element analysis(FEA)

TG115.5

A

0493-2137(2012)07-0651-05

2011-07-06；

2011-12-23.

国家自然科学基金资助项目(50975196)；高等学校博士学科点专项科研基金资助项目(20090032110026)；天津市科技支撑重点资助项目(11ZCKFGX03000)．

荆洪阳（1966— ），男，博士，教授，hjing@tju.edu.cn．

杨 祯，yzheng2131@gmail.com.