地铁通风空调系统的逐时优化节能控制策略

杨 昭，余龙清，马 锋，邵 敏

地铁通风空调系统的逐时优化节能控制策略

杨 昭，余龙清，马 锋，邵 敏

(天津大学机械工程学院，天津 300072)

针对地铁通风空调系统的负荷特点，提出节能控制目标逐时系统性能系数HSCOP及逐时优化策略．以某新建地铁车站为例，模拟分析了该优化控制策略及其节能效果．结果表明，与普通方案相比，采用所提出的逐时优化节能控制方案可使夏季典型日能耗降低9.4%，节能效果显著．

地铁通风空调系统；变频；自寻优；节能策略；优化

1 地铁通风空调系统节能控制关键参数分析

我国南北地域气候相差大、地铁设计理念不同，导致各地地铁车站通风空调系统的结构、参数有所差异．笔者以南方某地铁车站通风空调系统为具体研究对象进行分析和研究．

1.1 地铁通风空调系统组成及相关参数

典型的地铁车站通风空调系统原理如图1所示[4]．此地铁车站公共区间采用变风量(VAV)系统，即随着站内热湿负荷和站外空气参数的变化，通过变频调节空气处理机组(AHU)风机、回/排风机的转速来改变送/回风量，以满足站内乘客及工作人员的舒适性要求；通过冷水机组变容量、水泵变频变流量来匹配末端负荷．本系统初拟冷冻水采用一次泵变流量系统，冷却塔采用直交流式，根据冷却塔出水温度与空气湿球温度之差变频控制冷却塔风机风量[5-8]．由上述系统各部分运行方式可知该通风空调系统中的可变温度参数和可变质量(体积)流率参数如表1所示．

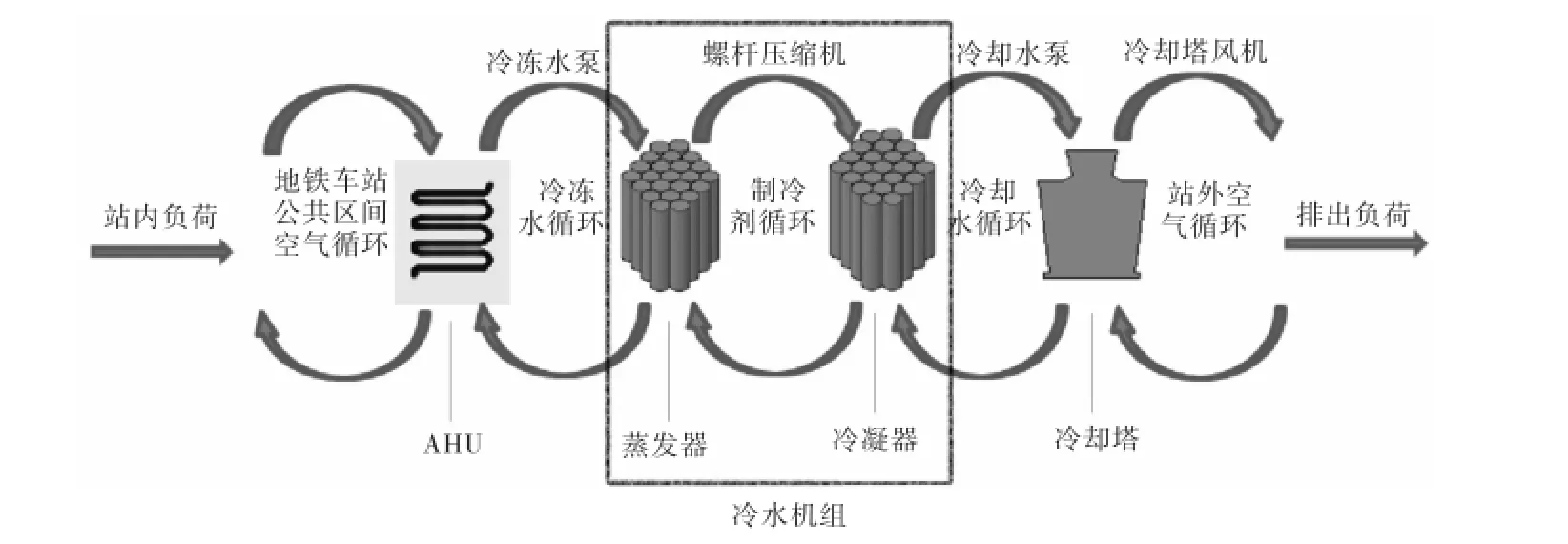
图1 地铁车站通风空调系统示意Fig.1 Schematic diagram of subway station’s HVAC system

表1 地铁通风空调系统中可变参数Tab.1 Variable parameters of the SVAC system in subway station

1.2 地铁通风空调系统节能控制关键参数的确定

AHU是通风空调系统中调节站内热湿环境的关键设备，相应的冷冻水供水温度和流量、AHU送风温度和风量是通风空调系统的重要参数．在确定的站内负荷和室外温度下，冷冻水供回水设计温差为5,℃时，由于AHU换热器和末端二通阀的共同作用，AHU送风温度与冷冻水供水温度共同决定送风量、相对湿度及冷冻水实际流量．同时，冷冻水供水温度和流量又决定了冷水机组的蒸发温度与蒸发压力．

冷却水供水温度tci由室外湿球温度tas和冷却塔风机风量共同决定．冷却水进出水温差为5,℃时，在确定的热负荷和室外湿球温度下，冷却水流量确定，冷却水供水温度为

故可通过温差Δtca控制冷却塔风机排风量来调节冷却塔出水温度tci．

由上述分析可知，在确定的负荷及室外条件下，表1中的各参数均可由tAHU、teo、Δtca三关键参数确定，从而决定了系统中各设备的功耗，因此该三参数为节能控制关键参数．

2 地铁通风空调系统逐时优化节能控制策略及方案

2.1 地铁通风空调系统节能控制普通方案

对系统设备单独进行变频控制是目前地铁通风空调系统常见节能控制方案(普通方案)，此时，tAHU、teo和Δtca三关键参数为既定常数．分析可知，当根据实际情况，使三关键参数在合理范围内联合波动可减少系统能耗：风机、水泵在变频允许范围内变化；AHU送风温度在(20±2)℃范围内变化；冷冻水供水温度在(7±1)℃范围内波动；冷却水进水温度与环境空气湿球温度间温差在3～5,℃波动．因此，可以利用合理波动的三关键参数来优化普通方案，提高通风空调系统的节能率．

2.2 通风空调系统逐时优化节能控制方案

三关键参数的变化对通风空调系统有着不同的影响．当tAHU降低时，可减少通风量，使AHU风机和回排风机能耗降低，也有利于保证AHU有效除湿，但是同时使蒸发温度降低、冷水机组能耗增加．

当环境湿球温度降低或者车站内负荷较小时，可以通过减少冷却塔通风量使温差增大来降低冷却塔能耗．但Δtca的增大使冷却水供水温度相对升高，导致冷凝器冷凝温度升高、冷水机组能耗增加．

因此，只有合理处理上述矛盾才能真正降低系统能耗，否则适得其反．本文针对地铁通风空调系统的负荷特点，着眼于地铁通风空调系统整体，提出了有效解决如上矛盾、实现节能控制优化的优化目标，即逐时车站通风空调系统能效比(HSCOP)为

式中：Q0为某1,h的站内热负荷，kJ；Nt为该小时通风空调系统总能耗，kJ．

基于以上分析，提出地铁通风空调系统节能控制优化方案，即地铁车站通风空调系统逐时优化策略逐时关键参数自寻优变频节能控制方案：以最大HSCOP值为优化目标，采用Visual Basic和Matlab混合编程，采集地铁站内数据和环境数据，在线自寻最优tAHU、teo、Δtca三关键参数，并以三关键参数为设定温度(差)，变频调节系统各设备，实现对地铁车站通风空调系统变风、水流量控制，减少系统整体能耗．

3 通风空调系统数学模型

利用上述的优化方案仿真通风空调系统．由于通风空调系统的设备数量多、结构复杂，设备之间存在较强耦合性(见图1)，且优化方案需快速在线寻优参数以指导系统运行，本文采用稳态法进行优化并计算节能效果．仿真计算所需各设备数学模型如下．

3.1 AHU空调箱模型

AHU空调箱采用整体串片型表面式换热器，冷冻水均匀流过肋管，空气在肋管外流动，假设空调箱与环境无热交换，则能量方程为

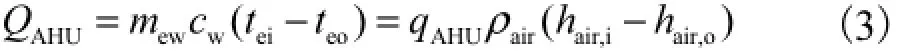
式中：cw为水的比热容，kJ/(kg·℃)；teo、tei分别为冷冻水供水和回水温度，℃；ρair为空气密度，kg/m3；hair,i、hair,o分别为AHU进、出口空气焓，kJ/kg．

传热方程可表示为

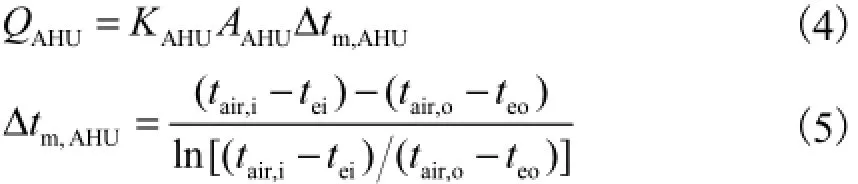
式中：KAHU为AHU换热器的传热系数，W/(m2·K)；AAHU为AHU换热器的换热面积，m2；tair,i、tair,o分别为AHU进、出口空气干球温度，℃．

热交换效率系数为

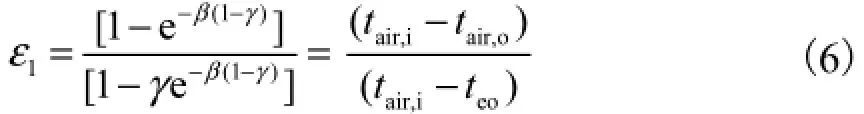
式中：β为传热单元数；γ 为两流体的水当量比．接触系数为

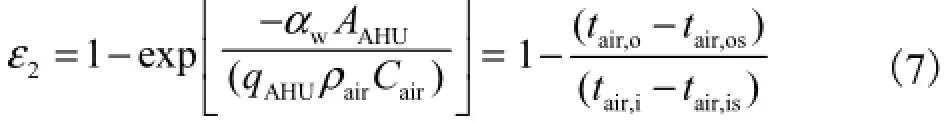
式中：αw为AHU换热器外表面传热系数，W/(m2·K)；tair,is、tair,os分别为AHU进、出口空气湿球温度，℃．

3.2 冷水机组模型

所研究地铁空调系统采用标准螺杆冷水机组[9]，主要包括螺杆压缩机、蒸发器、冷凝器和电子膨胀阀4部分．下面将分别介绍该4部分的数学模型．

3.2.1 螺杆压缩机模型

压缩机制冷剂质量流量可表示为

式中：ηv为压缩机容积效率；Vth为压缩机理论排气量，m3/h；νin为压缩机进口处的制冷剂比容，m3/kg．

压缩机出口温度为

式中：tcom，i为压缩机进口温度，℃；pcom,i、pcom,o分别为压缩机进、出口压力，Pa；n为多变过程指数．

压缩机电机功率为

式中：hcom,i、hcom,o分别为压缩机进、出口的制冷剂焓值，kJ/mol；ηel、ηme分别为电机效率和机械传动效率.

3.2.2 蒸发器模型

本冷水机组所选蒸发器为满液式．节流后的两相制冷剂从底部流入蒸发器，管外蒸发后从壳体顶部流出进入压缩机；冷冻水管内流动．假设壳体保温效果好，与环境无热交换，则能量方程为

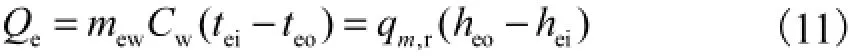
式中hei、heo分别为蒸发器进、出口处的制冷剂焓值，kJ/mol．

传热方程为

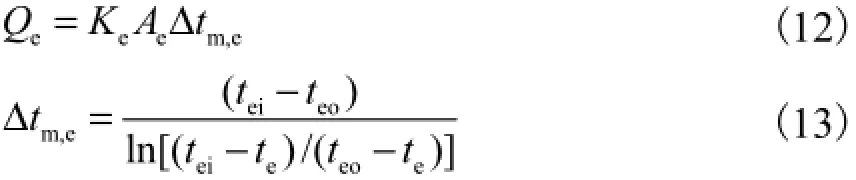
式中：Ke为蒸发器传热系数，W/(m2·K)；Ae为蒸发器传热面积，m2；te为制冷剂蒸发温度，℃．

3.2.3 冷凝器模型

本冷水机组冷凝器为卧式壳管式．压缩机排除的高温高压制冷剂从顶部进入，冷凝后的液态制冷剂从壳体底部流出；冷却水管外流动．假设壳体保温效果好，与环境无热交换，则其能量与传热方程与蒸发器相同．

3.2.4 电子膨胀阀模型

节流过程一般视为等焓过程，制冷剂制冷流率可表示为

式中：Cval为阀特性常数；ρin为阀进口处的制冷剂密度，kg/m3；val,ip、val,op分别为阀进、出口的制冷剂压力，Pa．

3.3 冷却塔模型

本通风空调系统选择了直交流式冷却塔，冷却塔冷却数为

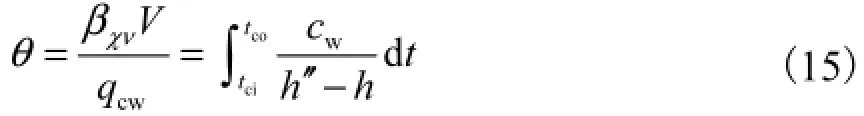
式中：βχν为散质系数；V为总填料体积，m3；qcw为冷却水体积流率，m3；h为空气焓值，kJ/mol；h′为饱和空气焓值，kJ/mol．冷却数计算时采用辛普逊积分法．

3.4 风机与水泵

通过变频改变风机与水泵的转速时，各参数按比例定律变化，即

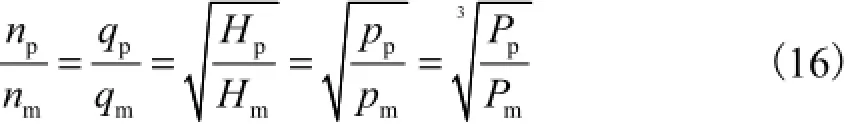
式中：q为水泵(风机)的流量，m3/h；H为水泵(风机)的扬程，m；p为水泵(风机)的全压，Pa；P为水泵(风机)的功率，kW；n为水泵(风机)的转速，r/min；下标p表示变频，m表示额定．

4 结果与分析

根据优化方案思路编制通风空调系统模拟程序，并以夏季典型日为例，计算分析该天工作18,h的优化结果．典型日气象参数如图2所示，空气干球温度最低接近29,℃，最高37,℃，湿球温度也在26,℃以上，全天气温较高．

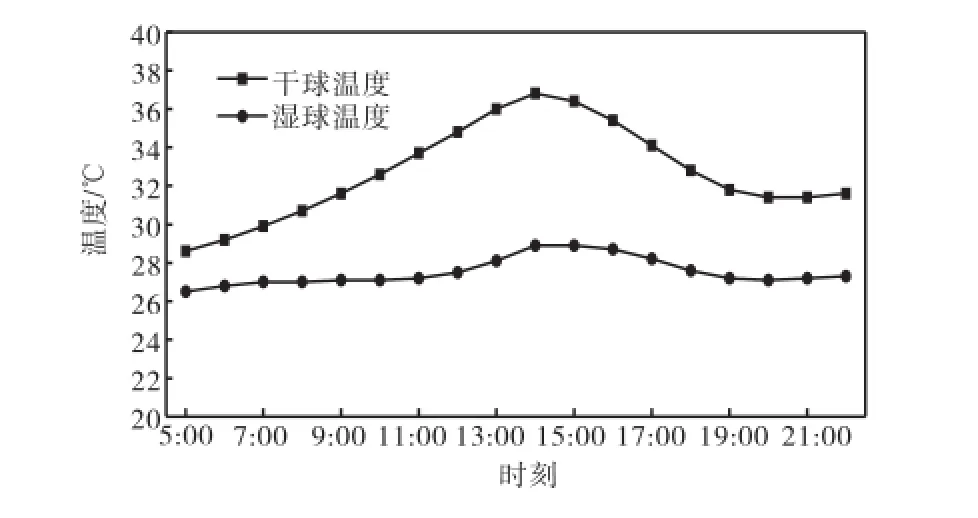
图2 夏季典型日气象参数分布Fig.2 Meteorological parameters′ distribution in the typical summer day

利用所编程序计算得到典型日的三可优化参数如图3所示，计算所得典型日的HSCOP值如图4所示，其中7：00至8：00时段为客流早高峰，17：00至18：00时段为客流晚高峰．由图3可以看出，AHU送风温度tAHU与冷冻水供水温度teo变化趋势相同，温差Δtca恒定为3,℃．

4.1 温度tAHU和teo

早晚高峰的AHU送风温度和冷冻水供水温度同时为最小值．此时段车站客流量大，通风需求量大，只有适当地降低送风温度才能有效减少系统能耗．但为了保证AHU的热交换效率和除湿效率，必须降低温度teo．其他时段，站内热负荷小，在满足降温除湿的同时，可根据实际情况优化参数tAHU和teo之间的匹配，使系统节能效果最优．

图3和图4表明，并非温度tAHU、teo越低，系统优化方案的节能效果越好．早晚高峰时段，优化前后系统能效比相差不大，主要原因是此时段站内通风量大，降低送风温度对通风量影响不大，反而增加冷水机组能耗，使系统整体节能效果不理想．其他时段，冷冻水供水温度teo高于设计温度7,℃，使蒸发温度升高、冷水机组能耗降低；AHU送风温度低于设计温度，虽变化较小，但仍降低风机能耗，从而提高系统能效比．

4.2 温差Δtca

图3中，温差Δtca恒定为3,℃，表明Δtca与环境温度、站内负荷均无关．然而，能耗最大(约占系统总能耗的50%)的冷水机组受冷却水供水温度影响，Δtca决定冷却水供水温度．只有Δtca尽量小，即冷却水供水温度最低，才能保证冷水机组功耗最小．同时经研究发现，冷却塔能耗相对较低(小于系统总能耗的3%)，所以小的温差Δtca可以有效降低系统的总能耗．由于温差Δtca=3,℃一般是冷却塔的冷却极限，且环境因素的不确定性使冷却塔变频变风量的可控性较差，所以不对冷却塔风机变频操作，即在额定功率运行．冷却塔风机不变频运行时的实际温差Δtca一般是大于3,℃的不确定值．

图3 夏季典型日三关键参数分布Fig.3 Three key parameters’ distribution in the typical summer day

图4 优化方案与普通方案HSCOP对比Fig.4 HSCOP comparison of optimization scheme and normal scheme

4.3 逐时系统能效比HSCOP及节能效果

由图4可知，夏季典型日优化方案和普通方案的最大HSCOP分别为2.72和2.45，最小值分别为2.32和2.18；优化方案HSCOP相对于普通方案平均提高了10.9%；优化方案节能量为270,kW·h，节能率9.4%．典型日里优化方案节能效果明显优于普通方案．

5 结 论

(1) 在地铁早晚高峰时段，AHU送风温度和冷冻水供水温度应设定为最小值；在非高峰时段，AHU送风温度和冷冻水供水温度可以小范围调整．

(2) 冷却塔风机能耗占系统总能耗的比例小，且其变频可控性差，因此不用变频控制，额定工况运行即可，此时温差Δtca是不确定值．

(3)提出了地铁通风空调系统逐时优化节能控制策略，三关键参数的实时动态优化使优化方案的节能效果明显优于普通变频方案．

［1］ Horita S，Kayama T，Nakamura T. Ventilation and airconditioning system design for the new Astram metro line in Hiroshima[J]. Mitsubishi Electric Advance，1996，74：11-14.

［2］ 中华人民共和国建设部. GB 50157—2003地铁设计规范[S]. 北京：中国计划出版社，2003. Ministry of Construction of People′s Republic of China. GB 50157—2003 Code for Metro Design[S]. Beijing：China Planning Press，2003(in Chinese).

［3］ 王 峰. 地铁通风空调系统变频节能研究[D]. 成都：西南交通大学机械工程学院，2007. Wang Feng. Study on Energy-Saving of Ventilation and Air-Conditioning System by Frequency Conversion in Subway[D]. Chengdu：School of Mechanical Engineering，Southwest Jiaotong University，2007(in Chinese).

［4］ 俞炳丰. 中央空调新技术及其应用[M]. 北京：化学工业出版社，2005. Yu Bingfeng. Central Air-Conditioning’s New Technology and Application[M]. Beijing：Chemical Industry Press，2005(in Chinese).

［5］ Sekhar S C. A critical evaluation of variable air volume system in hot and humid climates[J]. Energy and Building，1997，26(2)：223-232.

［6］ Yao Ye，Lian Zhiwei，Hou Zhijian，et al. Optimal operation of a large cooling system based on an empirical model[J]. Applied Thermal Enginneering，2004，24(16)：2303-2321.

［7］ Yu F W，Chan K T. Optimization of water-cooled chiller system with load-based speed control[J]. Applied Energy，2008，85(10)：931-950．

［8］ Gordon J M，Ng K C，Chua H T，et al. How varying condenser coolant flow rate affects chiller performance：Thermodynamic modeling and experimental confirmation[J]. Applied Thermal Engineering，2000，20(13)：1149-1159．

［9］ 伏 龙，丁国良，苏祖坚. 螺杆冷水机组稳态仿真[J]. 上海交通大学学报，2003，37(7)：1090-1093．Fu Long，Ding Guoliang，Su Zujian. Steady-state simulation of screw chillers [J]. Journal of Shanghai Jiao Tong University，2003，37(7)：1090-1093(in Chinese).

Hourly Optimization of the Energy Saving Control Strategy in Subway Ventilation and Air Conditioning System

YANG Zhao，YU Long-qing，MA Feng，SHAO Min
(School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

The energy saving control target’s hourly coefficient of system performance and hourly optimization strategy were proposed according to the loading characteristics of subway ventilation and air conditioning (SVAC)system. The strategy was used to simulate a new subway station and to analyze the energy saving effect of the optimization scheme. Results show that in a typical summer day，the amount of energy consumption in this scheme decreases by 9.4% compared with the normal scheme，so the optimization scheme has an obvious effect on the saving of energy.

subway ventilation and air conditioning (SVAC)system；frequency conversion；self-optimizing；energy saving strategy；optimization地铁通风空调系统约占地铁总能耗的40%[1]，其主要原因之一是一般按远期最大负荷设计并有一定富裕量[2]，而其运行特点是满负荷运行时间很短，一个工作日中负荷波动剧烈且早晚呈负荷高峰，长时间的部分负荷运行造成能量浪费严重．目前常用的节能措施是对通风空调系统流体机械进行变频控制，但因调节范围有限，所调参数相对独立，整体节能效果有待提高[3]．因此，笔者分析了此通风空调系统关键参数，提出了进一步的节能控制优化方案．

TK11

A

0493-2137(2012)07-0599-05

2011-03-09；

2011-05-27.

国家自然科学基金资助项目(51076112)；教育部博士点基金资助项目．

杨 昭（1960— ），女，教授．

杨 昭，zhaoyang@tju.edu.cn.