一种基于小波包分解FXRLS算法的自适应噪声抵消方法＊

金彦丰 余 毅

（91388部队92分队 湛江 524022）

1 引言

在舰船噪声控制技术领域，自适应噪声抵消（Adaptive Noise cancellation，简称 ANC）技术是一个重要研究方向［1］。时域ANC系统原理明了且结构简单，但收敛速度慢；而频域ANC系统频带和频带之间不相关，能很方便地将宽带噪声分割为多个频带分别抵消，具有更快的收敛速度和更宽的噪声抵消频带，且往往采取“块”FFT运算，计算量更低。上述特点决定了后者在复杂噪声抵消应用中更受重视。但傅立叶变换的固定频率分辨率使得频域ANC在抵消宽带噪声时也有其固有的局限性。而小波的先天时频多分辨能力使其成为更精细的噪声抵消技术的首选。小波包分解方法提供了全频段聚焦能力，分别对低频轮廓和高频细节按照相似的方法进行了划分，实现了对函数空间的任意树结构的分解［2～4］。

本文提出了一种基于小波包分解Filtered-XRLS（FXRLS）算法的自适应噪声抵消方法，并对该方法进行了分析和探讨。

2 算法推导

系统原理结构如图1所示，借鉴了时域、频域成功的经验，引入FX思想来降低次级通道的干扰。误差传感器接收到的信号可以表示为

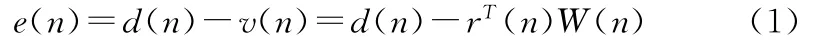
式中：r（n）被称为FX信号，由它组成的矢量被称为FX信号矢量；W（n）为权矢量。

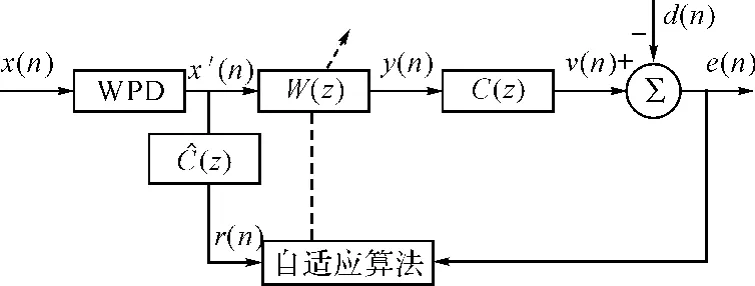
图1 自适应噪声抵消原理结构图

在控制宽带有色噪声时，RLS算法具有较快的收敛速度，对参考输入自相关矩阵的特征根散布不敏感，同时它的稳态失调非常小［5］。下面就来推导基于小波包分解的FXRLS算法［6］。

设置代价函数为一种误差指数加权形式：

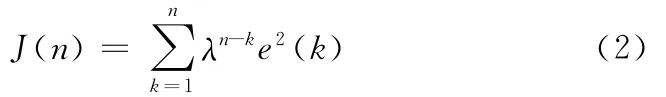
其中，e（k）为k时刻的误差信号。λ为遗忘因子，取值范围－1＜λ＜1，用于加权历史时刻的误差信号值：越是靠近当前时刻n的误差值，其在整个代价函数中的权重就越高，越是远离当前时刻的过去误差值，其权重就越低，故称作“遗忘因子”［7］。

将式（1）代入式（2）中得到：

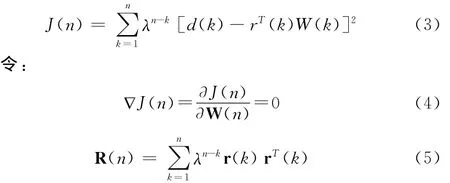
通过式（3）～式（6）联立可求得最优控制滤波器权矢量为

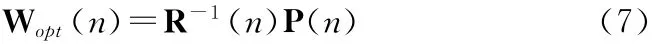
根据Woodbury求逆公式，有如下式成立：

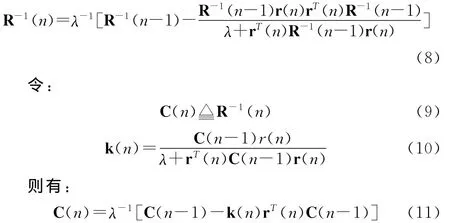
将式（11）代入式（10）中得到：

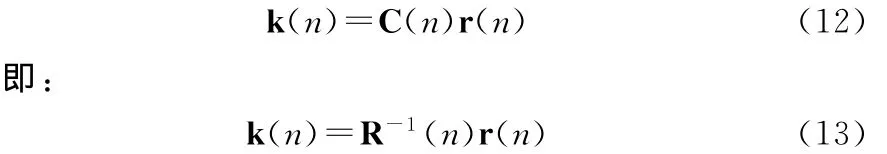
为了保证矩阵的正定和非奇异性，可以对代价函数作些修改：

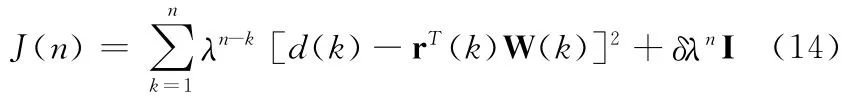
根据式（7），则有如下递推关系成立：

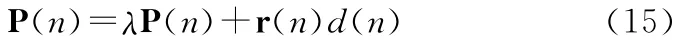
那么对式（7）中的最优权值进行迭代估计，则迭代公式为

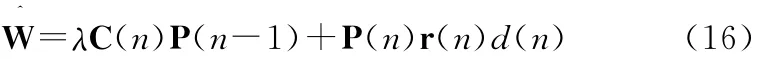
利用式（11）替换式（16）中的第一项，得到：

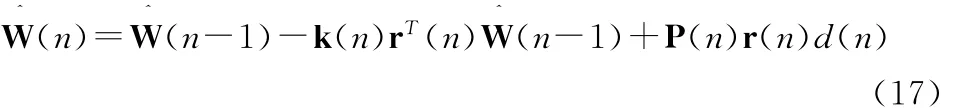
将式（11）代入式（17）得到：

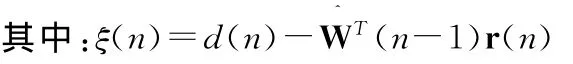
这就是指数加权递归RLS算法，它与传统域算法在迭代过程上并没有本质区别，只是公式中的某些变量是经过小波包分解后的结果。

3 仿真实验验证

3.1 线谱噪声ANC抵消仿真试验

首先进行多根线谱噪声的ANC仿真实验［8～9］，待抵消噪声的时域和功率谱如图2所示，仿真参数见表1，所有参数设置都以该方法抵消结果最优为原则，仿真结果如图3、图4所示。

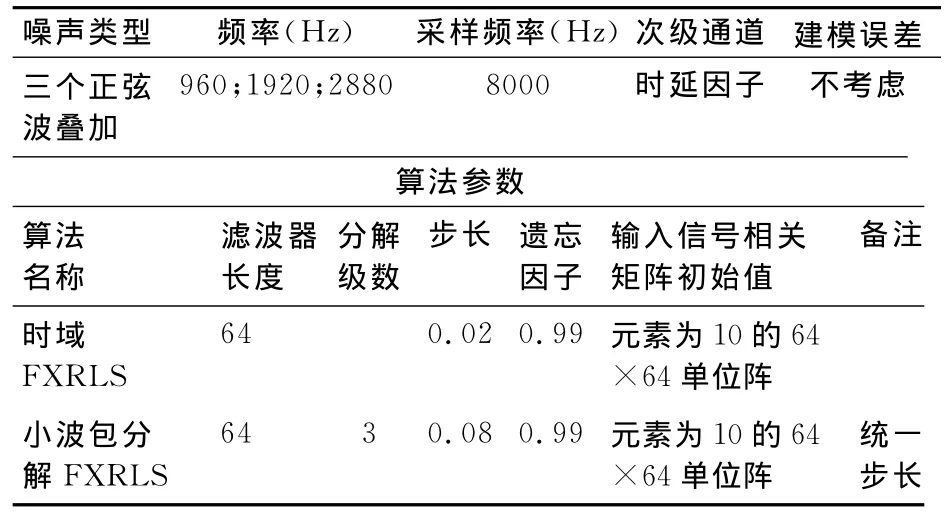
表1 线谱ANC RLS算法仿真参数

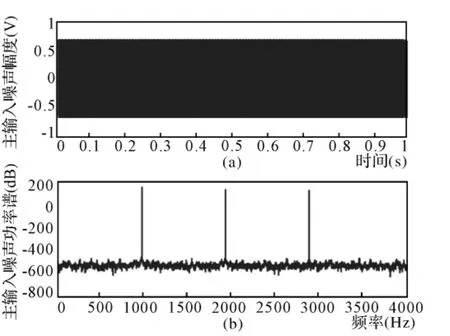
图2 主输入线谱噪声的时域图和功率谱图

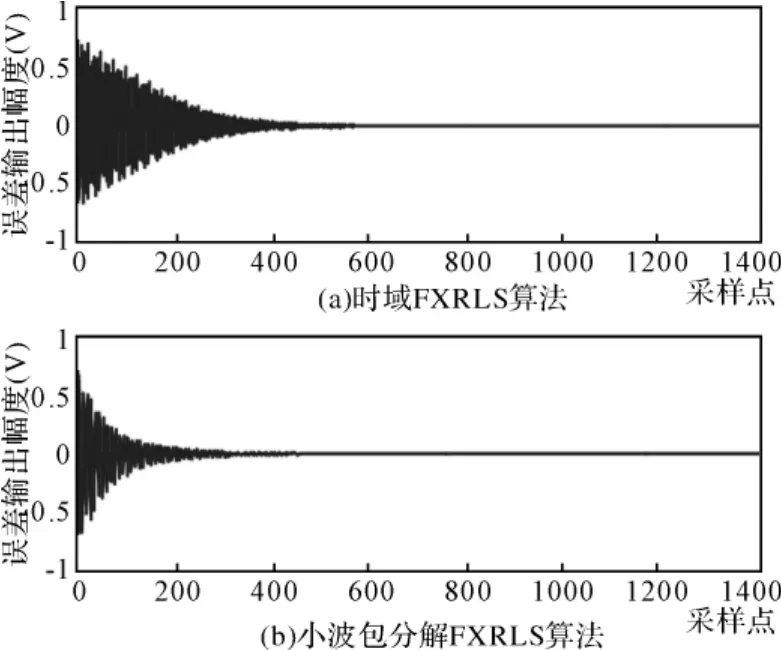
图3 线谱ANC RLS算法收敛速度对比图

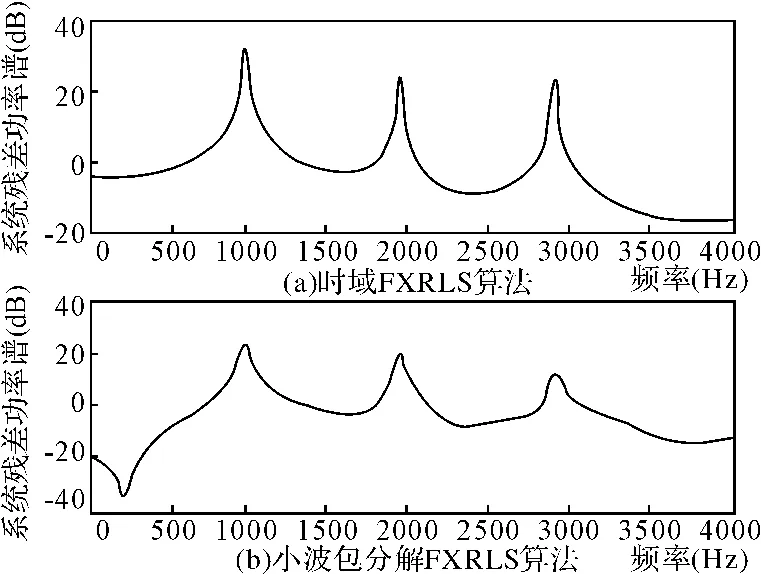
图4 线谱ANC RLS算法残差功率谱对比图

从图中可以看出，基于小波包分解的FXRLS算法收敛速度远快于时域算法，且有更高的降噪量和更低的稳态失调。经过计算，该算法的降噪量大于时域算法14dB。

3.2 连续谱噪声ANC抵消

下面进行宽带连续谱噪声的ANC仿真实验，待抵消噪声的时域和功率谱如图5所示，仿真参数见表2，所有参数设置都以该方法抵消结果最优为原则，仿真结果如图6、图7所示。

从图中可以看出，基于小波包分解的FXRLS算法比时域算法具有更快的收敛速度，且也有着更大的降噪量。系统收敛后，小波包分解的FXRLS降噪量为25.6dB，时域FXRLS算法的降噪量为20.05dB。

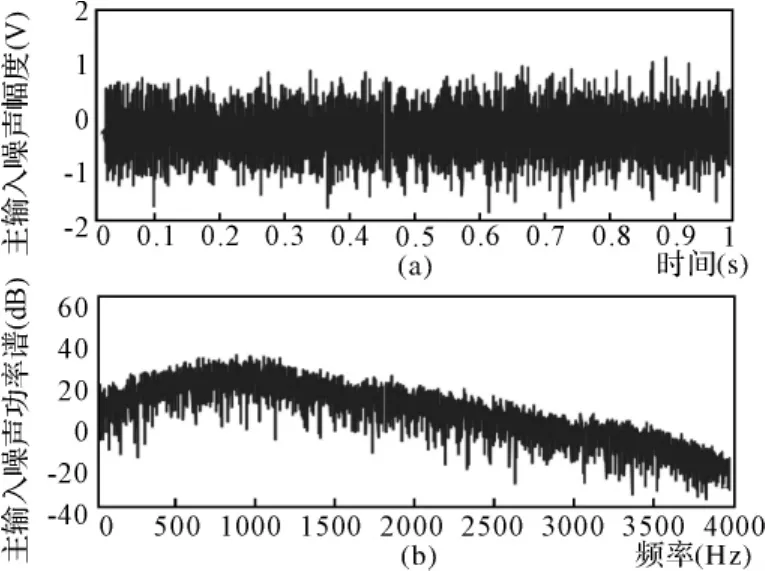
图5 主输入连续谱噪声的时域图和功率谱图

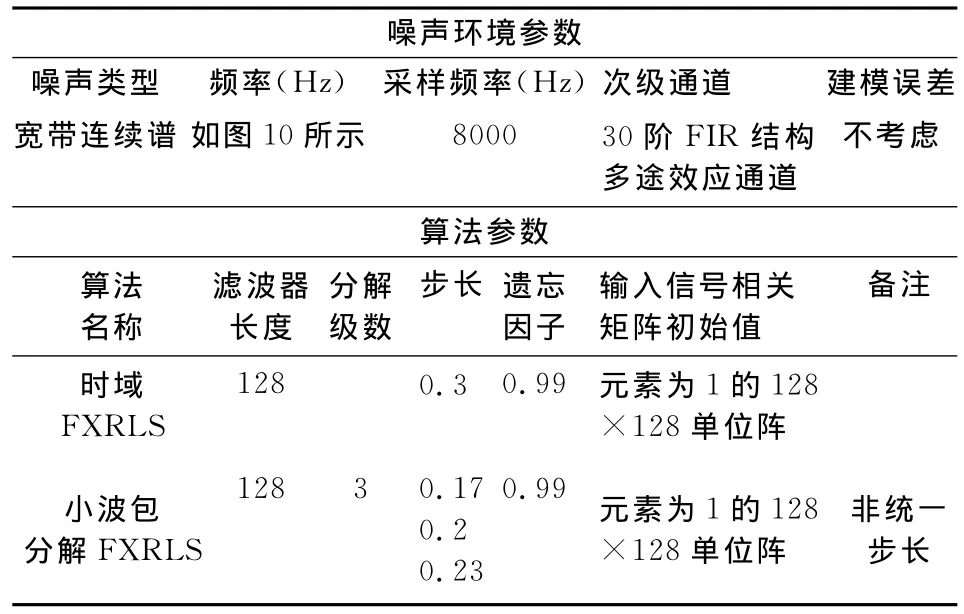
表2 连续谱ANC RLS算法仿真参数

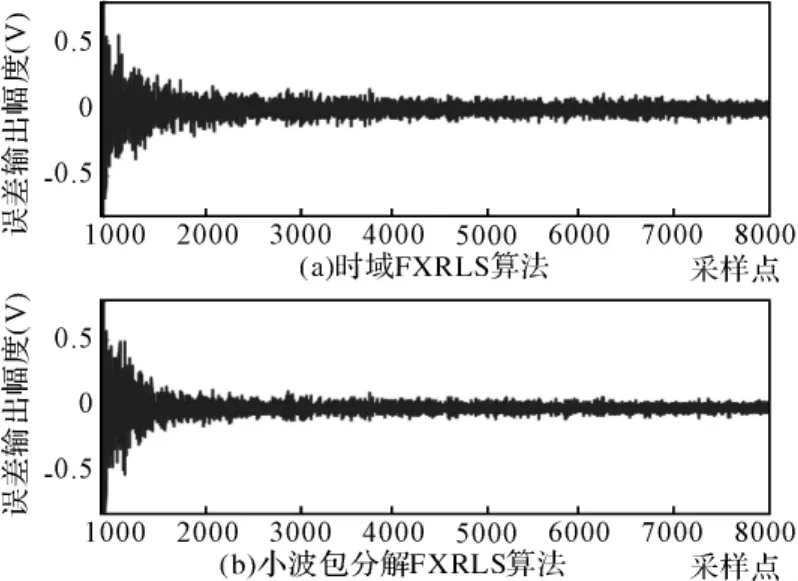
图6 连续谱ANC RLS算法收敛速度对比图

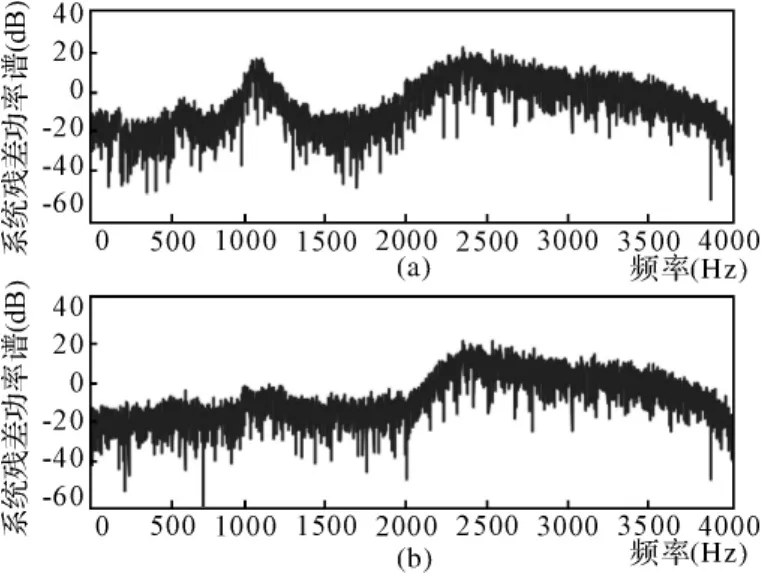
图7 连续谱ANC RLS算法残差功率谱对比图

4 海试验证

将时域ICA预处理技术和小波包分解ANC系统相结合，采用FXRLS算法，通过海试数据的处理来检验系统性能［10］。最后得到的噪声抵消结果如图8所示。

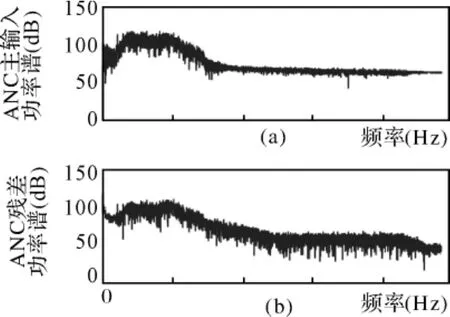
图8 基于小波包分解的ANC系统实验结果

主输入噪声和干扰噪声的相关系数为0.8；系统残差和干扰噪声的相关系数为0.065，也就是说，系统信号端基元附近的噪声和潜艇的干扰噪声的相关性已经大大降低，干扰噪声被抵消了。连续谱（0.05～0.4倍的归一化频率）降噪量为10.9dB；全频带降噪量为12.2dB。

5 结语

本文将基于小波包分解FXRLS算法应用于ANC领域，并进行了仿真实验和海试验证，结果表明：该方法比传统方法具有更好的噪声控制力。特别是海试数据处理结果，在较小的信号失真度情况下，取得了约12.2dB的全频带降噪量。进一步表明该方法能够处理复杂的水下噪声主动抵消问题。

［1］刘伯胜，雷加煜.水声学原理［M］.哈尔滨：哈尔滨工程大学出版社，1997：232-238.

［2］张子瑜，陈进，史习智.一种基于小波级数分解的LMS自适应除噪方法［J］.振动工程学报，1999，12（1）：73-77.

［3］吴婷，颜国正，杨帮华.基于小波包分解的脑电信号特征提取［J］.仪器仪表学报，2007，28（12）：2230-2234.

［4］谢松云，潘辉，张伟平结合小波包和ICA的脑电信号特征提取方法［J］.计算机应用研究，2008，25（9）：2671-2673.

［5］Simon Haykin.Adaptive filter theory［M］.Beijing：Publishing House of Electronics Industry，2002：94-128.

［6］Dennis R Morgan，Charles Sanford.A control theory approach to the stability and transient analysis of the Filtered-X LMS adaptive notch filter［C］／／IEEE Transactions on Signal Processing.1992，40（9）：2341-2346.

［7］肖鹏韬.基于遗传算法的RLS自适应算法研究［J］.电子测试，2010（5）：16-19.

［8］张翼鹏，何正耀.舰船辐射噪声建模与仿真研究［J］.电声技术，2005（12）：52-55.

［9］胡伟文，肖锋，苑秉成.目标辐射噪声线谱的特征建模与检测［J］.海军工程大学学报，2006，18（6）：45-48.

［10］吴英姿，鲍雪山，徐新盛.应用频域ICA对参考输入进行预处理的 ANC系统［J］.振动与冲击，2008，27（8）：81-84.