基于PSOPCNN的图像滤波算法＊-

柳志忠

（海军驻葫芦岛431厂军事代表室 葫芦岛 125004）

1 引言

将粒子群算法（PSO）的基本原理融入到PCNN图像滤波算法中，从而得到了一种适用于PCNN图像滤波的粒子群算法，主要考虑PCNN图像滤波算法的连接系数β、连接系数β及预设阈值V0的参数确定问题，通过粒子群优化算法在解空间里寻求最优解。本文就粒子群算法（PSO）、PSO-PCNN算法、仿真与实验结果分析等，作进一步的研究和探讨［1］。

2 粒子群算法（PSO）

PSO粒子群优化算法（Paritcle Swarm Optimization）具有简单、较容易实现，具有一定智能化程度，既方便用于科学研究又可用于工程应用等多方面优势。在PSO算法中过程，搜寻区域中的一个“目标”的过程即是求解每个优化问题的解的过程，这个“目标”被称为粒子，自己的位置向量和速度向量是每个粒子都具有的特征，每个位置都表示了一组参数值。对于一个D维的优化问题，设一个D维空间中的每一个位置的粒子都代表优化问题中的一个解，而位置就代表着等待被算法优化调整的参数。所有的粒子都有一个适应值（fitness value），被优化的函数决定了该适应值的大小，每个粒子都有一个飞行速度，该速度决定了他们飞翔的方向和距离。然后粒子们就对区域中当前的最优“解”进行搜索［2］。

PSO算法的初始化是对一群随机粒子随机的进行的，然后利用迭代的方法寻找最优解。在每一次迭代过程中，粒子通过跟踪两个“极值”来对自己进行更新。第一个就是基于粒子自身所找到的最优解，称为个体极值pi；另一个是整个群体当前所能找到的最优解，称之为全局极值pg。此外，在局部群体中找到的最优解，称之为局部极值。

根据对环境的适应度，PSO算法将群体中的个体（粒子）移动到预想的区域，然而该算法不像其他优化算法那样只优化某个个体，而是把每个个体当作D维搜索空间中的一个无质量、无体积的点（粒子），以一定的速度在D维空间中飞行。然后分别根据它自身和同伴的运动经验来动态调整飞行速度。

粒子群算法采用以下的数学描述进行定义：假设在一个D维的目标搜索空间中，有一个粒子群是由N个代表潜在问题解的粒子组成的，用一个D维的向量表示其中第i个粒子。飞行速度是vi＝［vi1，vi2，…，viD］T；在D 维的搜索空间中第i个粒子的位置是xi，xi＝［xi1，xi2，…，xiD］T，i＝1，2，…，N；第i个粒子当前搜索到的个体最优位置记为pi，pi＝［pi1，pi2，…，piD］T；粒子群当前搜索到的全局最优位置记为pg，pg＝［pg1，p2，…，pgD］T。PSO 算法对粒子的操作采用下列公式进行：

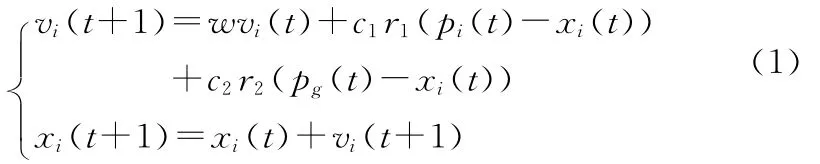
式中，i＝1，2，…，N；t为迭代代数；w 为加权因子，取值在0.1～0.9之间；c1，c2为学习因子，一般取值为2；r1，r2是对角线元素是在［0，1］之间均匀分布的随机数组成的D×D维的对角线矩阵。为了把vi（k）和xi（k）的值控制在合理的区域内，有必要用参数进行限制。式（1）可以决定粒子下一步的运动速度和粒子坐标。这样的调整将使粒子在两个最优位置周围进行搜索。

3 PSO-PCNN算法

PCNN的图像滤波方法的处理过程是，首先对图像中的噪声像素进行精确定位，然后判别是否为噪声像素，如果是有用信息，则根本不做处理，如果是噪声，在对其进行类中值方法的滤波处理，这样就能从根本上最大限度的保留住有用的信息像素，使图像经过滤波后只能是向着原图的方向渐渐靠拢，这样在保持有用信息不被认为破坏的前提下，尽可能的滤除了噪声污染，从而大大提高滤波性能［3］。

对于神经网络优化，粒子群算法主要包括两个方面：一是优化网络各层之间的连接权值；二是对于网络的拓扑结构进行优化。本章算法中确定的适应度函数可用原始训练图像和加噪滤波后的图像的平均绝对误差的倒数来表示：

按照式（2），粒子群算法对PCNN模型参数自动确定的工作流程可表示如下：

1）随机产生初始粒子群，即可用xi和vi分别表示第i个粒子的位置和速度；

2）通过激活PCNN神经网络，根据粒子的位置对加噪图像进行滤波，确定适应度，计算每个粒子的适应值fitness；

3）将第i个粒子适应值与该粒子曾经经历过的自身最优位置pi的适应值作计算比较，如果其结果较好，则把该粒子当前对应的位置当作目前的最优位置pi；

4）将每个粒子当前的适应度与粒子群目前的全局最优位置pg的适应度作比较，计算结果如果较好，则将目前比较出的粒子对应的位置作为全局最优位置pg；

5）根据计算出的速度、位置的最新值更新公式（1）来改变粒子的速度和位置；

6）当优化终止条件（终止条件通常为足够好的适应值或达到一个预设的足够多的迭代次数）被满足时，则输出结果；否则返回第2步继续循环，直到满足终止条件为止。

4 仿真与实验结果分析

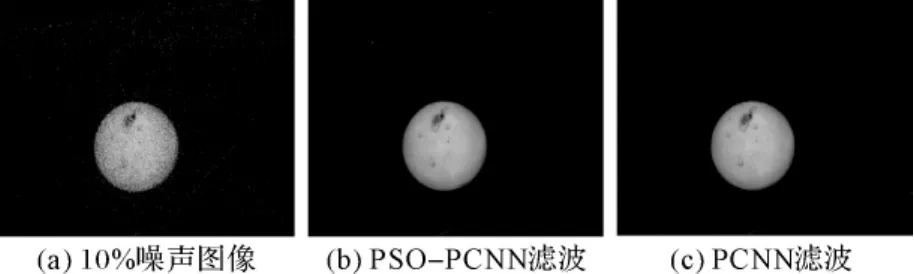
图1 10%噪声水下球体图像的滤波结果比较

图2 20%噪声水下球体图像的滤波结果比较

以水下球体图像为例，分别在10%和20%噪声强度下采用PSO-PCNN滤波和PCNN滤波，并对二者进行了比较。其仿真结果如图1和图2所示［4］。

根据上述算法，为了节省仿真时间，采用以下PSO参数：进化代数为2，种群中的粒子总数p＝10，权重因子w＝0.1，最大速度Vmax＝24.6。PSO在不同噪声强度下对PCNN参数的自动确定数据如表1所示。

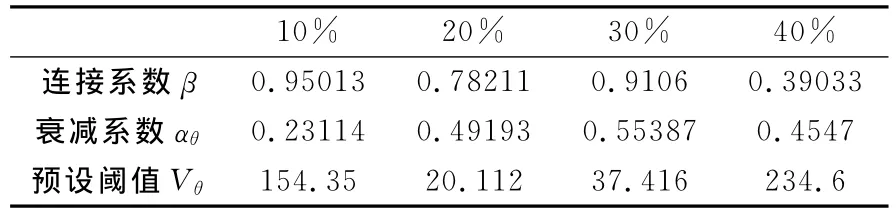
表1 PSO在不同噪声下自动确定的PCNN参数

对水下球体图像分别加10%、20%、30%和40%强度的噪声，比较PSO-PCNN滤波和PCNN滤波的平均绝对误差MAE的大小，如表2所示。

表2 对水下球体图像加不同噪声强度时采用两种滤波方法的MAE性能比较

通过计算机仿真，从图1和图2中对两种算法的滤波效果进行比较，可以得出这样的结论：基于PSO的PCNN图像滤波方法在去噪能力方面表现得比PCNN滤波方法要强一些，而且对PCNN模型中的参数也能够很好的实现自动确定，不必手工设置PCNN参数。此外，从表1、表2的比较，也能够得出：PSO-PCNN滤波方法比PCNN滤波的效果好得多。所以，总的看来，就滤波算法而言，PSOPCNN算法的滤波性能要优于PCNN滤波，能够对PCNN模型中的参数实现自动确定，具有更强的适应性。

5 结语

在PCNN模型的参数需要反复试验的前提下，提出了基于PSO的自动确定参数的PCNN图像去噪算法。以水下球体图像为例，加以不同程度的脉冲噪声，将其与PCNN滤波进行比较；并对两种算法的平均绝对误差MAE的对比曲线进行仿真。结果表明，当噪声密度在10%～40%之间时，PSO-PCNN滤波的平均绝对误差明显比PCNN法小得多，PSO-PCNN滤波比PCNN滤波方法的效果好［5］。

［1］孙小强，张求明.一种基于粒子群优化的多目标优化算法［J］.计算机工程与应用，2006（18）：40-42，78.

［2］郑思平，陈红周.一种加入创新粒子的粒子群［J］.数学理论与应用，2010（1）：14-17.

［3］邢杰，萧德云.混合粒子群优化算法及其应用［J］.化工学报，2008（7）：1707-1710.

［4］王力维.基于粒子群优化算法的神经网络钻削参数优化［J］.科技信息（科学教研），2007（25）：344-538.

［5］张赫，徐玉如，万磊，等.水下退化图像处理方法［J］.天津大学学报，2010，43（9）：827-833.