基于四阶累量对角切片谱的线谱估计方法＊

王克刚 杨 鹏

（1.解放军第421医院 广州 510000）（2.海军兵种指挥学院 广州 510430）

1 引言

辐射噪声特征提取研究在水中目标的探测和识别中具有重要意义。在众多的辐射噪声特征参数中，由一系列旋转机械产生的低频线谱成分显得尤为重要。Lofar谱图分析是较具代表性的被动水声信号处理方法之一。该方法通过对连续的采样数据作短时傅里叶变换而构成信号表达的三维立体图，可反映信号的非平稳特性。Lofar谱图分析是基于信号的功率谱。而基于高阶统计量的四阶累量对角切片谱，由于是基于信号四阶谱的一种特殊情况（对角切片），因此它既保留了高阶谱可抑制加性高斯噪声的优良特性，同时谱结构与功率谱相同［1］。文献［2～3］利用1谱进行谱图分析，取得了一定效果，但1谱与功率谱结构不一致并且不能滤除相位耦合的信号。因此，可以利用四阶累量对角切片谱进行Lofar处理，得到四阶累量对角切片谱图。对谱图进行分析，得到线谱特征。

2 四阶对角切片谱的定义和性质

对于随机变量x（t），定义四阶累量对角切片维谱C（ω）为变量x（t）的四阶累积量c4x（τ1，τ2）的对角切片c4x（τ，τ）的傅里叶变换，即［4～6］：

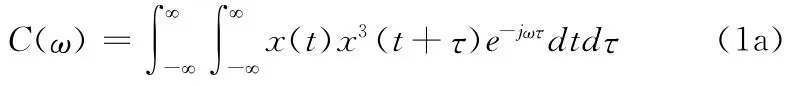
其具体计算式如下：

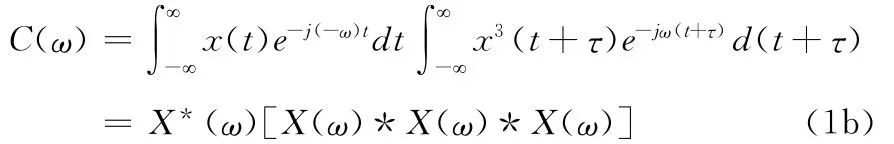
其中X（ω）为x（t）的Fourier变换，X＊（ω）为 X（ω）的复共扼，符号＊表示卷积。

四阶累量对角切片谱具有以下性质［2］：

证明：由四阶累积量的定义，并结合φi是［－π，＋π）内均匀分布的随机变量，可得：

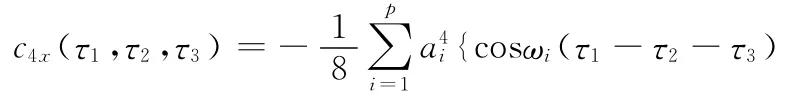
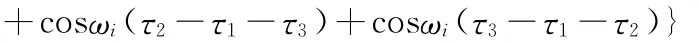
那么：

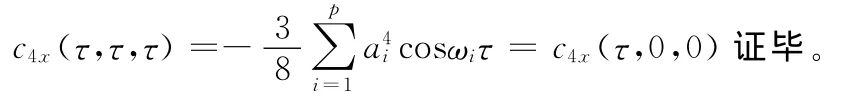
性质2：设n（t）为零均值的高斯噪声，则有：C4n（ω）≡0。

性质3：设n（t）是均值为零的随机噪声，任何两个不同时刻都互不相关，且概率密度函数f（n）为对称分布，则有：

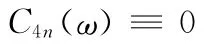
并结合φi是［－π ＋π 内均匀分布的随机变量，可得：

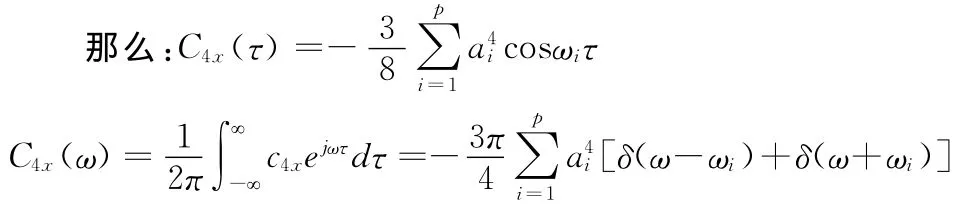
证毕。

3 LOFAR谱图

为了提高在低信噪比下线谱检测、跟踪和提取能力，必须利用多行的数据，推迟决策，即进行LOFAR处理［7］。被动声纳通常是将在某个方向上接收的信号进行时频分析，并将分析的结果显示给观察者。若用x轴表示信号的频率，y轴表示时间，亮度表示幅度。这种表示时频平面的M×N二维图像就是LOFAR谱图。

LOFAR谱图分析是近10年以来的较具代表性的被动声纳信号处理方法之一。文献［8］介绍了获得LOFAR谱图的方法，具体步骤如下：

1）将原始信号的采样序列分成连续的若干段，每段N个采样点。根据具体情况，段可部分重叠。

2）对每段信号采样样本L（n）作归一化和中心化处理。归一化处理的目的是使接收信号的幅度（或方差）在时间上均匀；中心化处理是为了使样本的均值为零。

3）对信号x（n）作短时傅里叶变换得到Lofar谱图

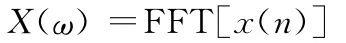
4 四阶累量对角切片谱图及线谱检测方法

Lofar谱图是对信号作分段的短时傅里叶变换得到的。而由前面的分析可知，四阶累量对角切片谱维谱比傅里叶变换具备更好的高斯噪声抑制性。

4.1 四阶累量对角切片谱图

假设原始信号s（t）采样率为fs，获得四阶累量对角切片谱图的具体步骤如下：

1）将原始信号的采样序列分成连续的若干段L（n），每段N个采样点。根据具体情况，段可部分重叠，设重叠M个采样点。

2）对每段信号采样样本L（n）作归一化和中心化处理。归一化处理的目的是使接收信号的幅度（或方差）在时间上均匀；中心化处理是为了使样本的均值为零。

3）按照式（1）对信号x（n）作K点四阶累量对角切片谱维谱得到谱图。

4.2 线谱检测方法

窄带信号在谱图上表现为线谱。线谱除了在谱的形状，如幅值高、满足一定的斜率和宽度要求外，在时间会持续一段时间。在谱图上，由线谱点组成的点形成了一条清晰的亮线，即谱线。这样，本来是一维的频率检测和跟踪问题，在谱图上就变成了谱线检测和提取问题。

本文采用图像处理方法进行线谱提取。使用Radon变换来检测谱图中的谱线。当谱线为直线时，该方法在低信噪比下有很强的提取能力。

将（x，y）图像平面的一条直线ρ＝xcosθ＋ysinθ映射成Radon空间的一个点（ρ，θ），连续图像的Radon变换定义为［9～10］：

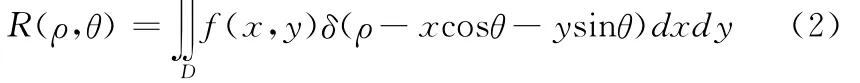
其中：D 为整个图像平面；f（x，y）为图像上（x，y）像素点灰度值；δ为狄拉克函数；ρ为（x，y）平面直线到原点距离；θ为原点到直线的垂线与x轴的夹角。

对于Radon空间点（ρ，θ），可以使用下式重构原图像空间直线：

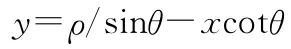
这样，就可以根据直线参数得到线谱的频率和调频率。具体公式如下：

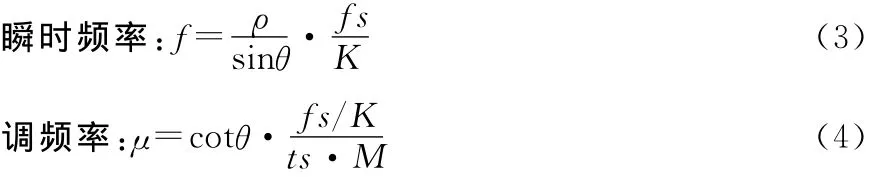
5 仿真实例

为验证本文方法的实际效果，下面给出一个基于Matlab工具的仿真实例。

原始信号：

采样率为1500Hz，信号时长为13.89s。f0＝20Hz，f1＝120Hz，μ1＝5Hz／s，f2＝500Hz，μ2＝－8Hz／s。噪声为加性白噪声，信噪比为－8dB。

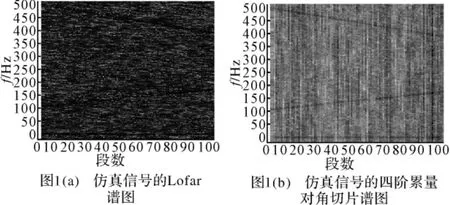
按照3节和4.1节的步骤计算得到Lofar谱图、四阶累量对角切片谱图如图1所示。

如图1（a）所示，信号的Lofar谱图中无法分辨出线谱；而图1（b）中可以看到存在3条亮线。这说明四阶累量对角切片谱谱比Lofar谱图具有更强的白噪声抑制功能。分别对Lofar谱图、四阶累量对角切片谱图作Radon变换如图2所示。

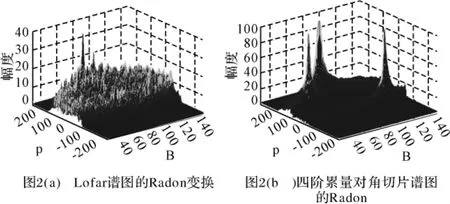
如图2所示，Lofar谱图的Radon变换只有一个较为明显的峰值，四阶累量对角切片谱图的Radon变换有三个峰值。这也说明四阶累量对角切片谱图具有良好的白噪声抑制能力。

Radon变换将直线转换为峰值，得到峰值在Radon平面中的点坐标（ρ，θ），通过式（3）和式（4）计算可以得到谱线的参数。其结果见表1。

表1 线谱参数表

使用Lofar谱图在仿真条件下无法识别所有线谱。文中提出的方法能够取得较好线谱检测和参数提取的效果。

6 结语

本文从四阶累量对角切片谱的性质出发，分析了Lofar谱图的计算方法。为了利用高阶谱的优势，将Lofar处理中的功率谱计算使用四阶累量对角切片谱维谱替代，介绍了四阶累量对角切片谱图的计算方法。得到四阶累量对角切片谱图后，使用Radon变换检测谱图中的直线，并得到直线的相关参数，计算线谱的频率和调频率。最后仿真表明该算法效果明显。

［1］张贤达，保铮.非平稳信号分析与处理［M］.北京：国防工业出版社，1998：153-178.

［2］陈鸣，杨鹏，苑秉成.基于1谱的水中目标辐射噪声线谱估计方法［J］.舰船科学技术，2010，33（10）：62-64，98.

［3］Peng Yang，Bing-cheng Yuan，Sheng Zhou.An Line Spectrum Estimation Method of Underwater Target Radiated Noise base on the 1D Spectrum［J］.CICC-ITOE 2010，2010，1：297-301.

［4］Chow T W S，Tan H Z.HOS-based nonparametric and parametric methodologies for machine fault detection［J］.IEEE Transactions on Industrial Electronics，2000，47（5）：1051-1059.

［5］樊养余，孙进才，李平安，等.基于高阶谱的舰船辐射噪声特征提取［J］.声学学报，1999，24（6）：611-616.

［6］梁红，王惠刚，李志舜.基于四阶混合累积量的自适应线谱增强器［J］.西北工业大学学报，2003，21（1）：50-53.

［7］李琴，苑秉成，张文娟.舰船辐射噪声建模及仿真模拟器的实现［J］.舰船科学技术，2010，32（4）：50-53.

［8］熊紫英，朱锡清.基于LOFAR谱和DEMON谱特征的舰船辐射噪声研究［J］.船舶力学，2007，11（2）：300-306.

［9］Wood J C，Barry D T.Radon transformation of time-frequency distributions for analysis of multicomponent signal［J］.IEEE Transactions on signal processing，1996，42：3166-3177.

［10］冉鑫，马世伟，曹家麟.基于Radon-Wigner变换的多分量LFM信号的检测［J］.上海大学学报（自然科学版），2001，7（2）：119-122.