基于改进小波算法的舰炮齿轮箱故障特征提取*
2012-06-07王凯
王 凯
(海军驻郑州地区军事代表室 郑州 450015)
1 引言
舰炮的齿轮箱承受着扭转和拉压两种载荷的综合作用,受力过程非常复杂。因此,舰炮的许多故障出现在齿轮箱里的齿轮和传动轴中。据统计,以齿轮为代表的齿轮箱故障发生率占舰炮机械故障的49%~58%[1]。由于舰炮自身结构复杂,在其振动信号中不同零部件的故障频率分布在不同的频段范围内。因此,当齿轮箱出现早期故障时,其微弱的故障信息往往会被淹没在其他零部件的振动信号和随机噪声中。
小波分析具有优良的时频分析特性[2~3],在时-频相平面的高频段具有较高的时间分辨率和低的频率分辨率,而在低频段具有低的时间分辨率和高的频率分辨率,克服了傅立叶变换中时-频分辨率不变的弱点,能在具有足够时间分辨率的前提下能对信号中的短时高频成分进行分析,又能在很好的频率分辨率下对信号中的低频进行估计,适合于提取非平稳信号和时变信号的特征,为机械故障诊断中的非平稳信号分析、弱信号提取和信号滤波等提供了一条有效的途径[4~10]。然而研究发现,在对信号进行小波变换时会存在严重的混频现象,这种现象往往会掩盖信号中的故障特征,尤其在提取微弱故障特征时表现更为明显。
2 小波分解算法及其产生混频的原因
2.1 小波分解算法
小波变换实际上就是将时域信号投影到尺度和时间组成的二维时频空间中,假设有一平方可积函数ψ(t)∈L2(R),其中L2(R)表示平方可积的实数空间,即能量有限的信号空间。若ψ(t)的傅立叶变换Ψ(ω)满足允许性条件:

则我们称Ψ(t)为一个基本小波或母小波(Mother Wavelet)。将母函数Ψ(t)经伸缩和平移后就可以得到一个小波序列。
对于连续的情况,小波序列为
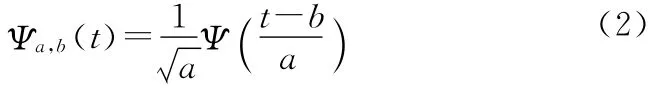
其中a为伸缩因子,b为平移因子,且a,b∈R;a≠0。对于离散的情况,小波序列为
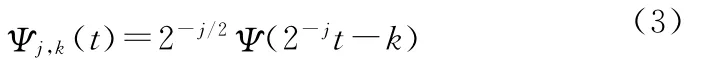
其中j,k∈Z。
对任一信号f(t)∈L2(R)的连续小波变换定义为
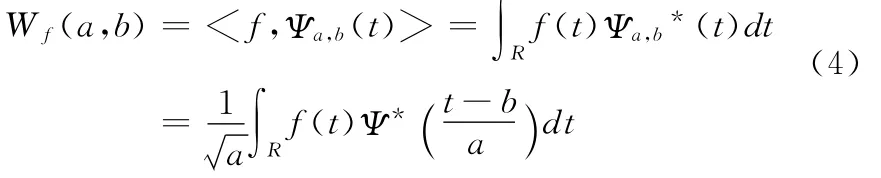
式中:〈,〉表示内积,*表示共轭。
从式(4)可看出,如果把小波函数看成是L2(R)空间的基函数系,那么小波系数就是信号在基函数系上的分解或投影。涉及到具体的算法,其实质是将待分解信号通过一组低通滤波器h(n)和高通滤波器g(n)进行滤波,得到一组低频信号和一组高频信号,并且对低频信号一直分解到第N层,如图1所示。
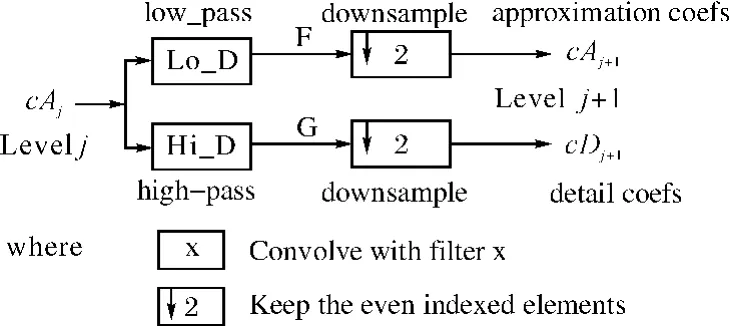
图1 小波分解算法
由于每次分解所得到的低频信号和高频信号长度都是原信号长度的一半,而且两者长度之和等于原信号的长度,所以分解结果既不冗余,也不损失原信号的任何信息。根据小波分解后的各个分量能够包含原信号所有特征这一特点,对采集的信号进行若干次小波分解就可以得到信号在不同频段上的分量,从而实现信号特征的分离。
2.2 小波分解算法产生混频的原因
从以上小波分解算法可知,小波变换中有与滤波器卷积这一环节。如果要分解后各频带的信号能正确地提供相应的频谱信息,则需要高通滤波器Hi_D及低通滤波器Lo_D具有理想的截止滤波特性。然而实际情况并非如此,如图2所示为db5小波的低、高通滤波器的频率响应图。
从图中可看到它们的频带都大大扩展了,高、低通滤波器能量不集中、衰减不迅速,造成了频谱泄露,通过尺度变化后,各频带会出现重叠现象,使得信号的某些频率成分将会在小波变换的相邻尺度下重复出现,信号通过滤波器后接有隔点采样运算必然出现混叠效应,某些该滤去的频率没有滤去,从而产生了虚假的频率成分。
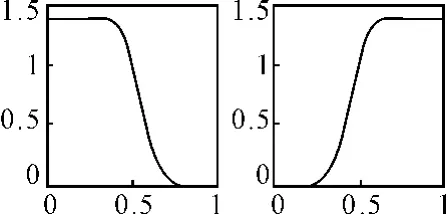
图2 db5小波的滤波器频域特性
3 小波分解算法混频的消除
从以上的理论分析可以看出,直接对信号进行小波分解会产生一些虚假频率。因此,本文针对这一问题提出一种改进的小波分解算法,使得分解后的信号能够正确地反映原信号的频谱分布信息。设信号采样频率为fs,其流程图如图3所示。
4 故障特征提取步骤
表征舰炮齿轮箱故障的特征参量有很多,如何从信号中提取那些对于故障高度敏感、可靠的特征参量是至关重要的。当舰炮齿轮箱发生故障时,它的振动信号中的许多统计特征都会随着故障的性质及严重程度而发生变化,而且不同的故障会在相应的频带上会有所反映。因此,在以上研究的基础之上,本文提出一种基于改进小波算法的舰炮齿轮箱故障特征提取方法,即对采集的齿轮箱振动信号,利用前面提出的改进小波变换的方法对其进行若干层分解,计算各个频率段信号的能量占该信号总能量的百分比,从而提取出信号的故障特征参量。具体步骤如下:
1)首先选择小波基函数,并依据要分析信号的特点以及采样频率的大小确定要分解的层数N;
2)对采集到的振动信号进行N层正交小波分解,得到从低频到高频的小波分解系数序列{aN,dN,dN-1,…,d1};
3)求各频带信号的总能量。设Edk为第k层高频小波分解系数序列dk的能量,则有:
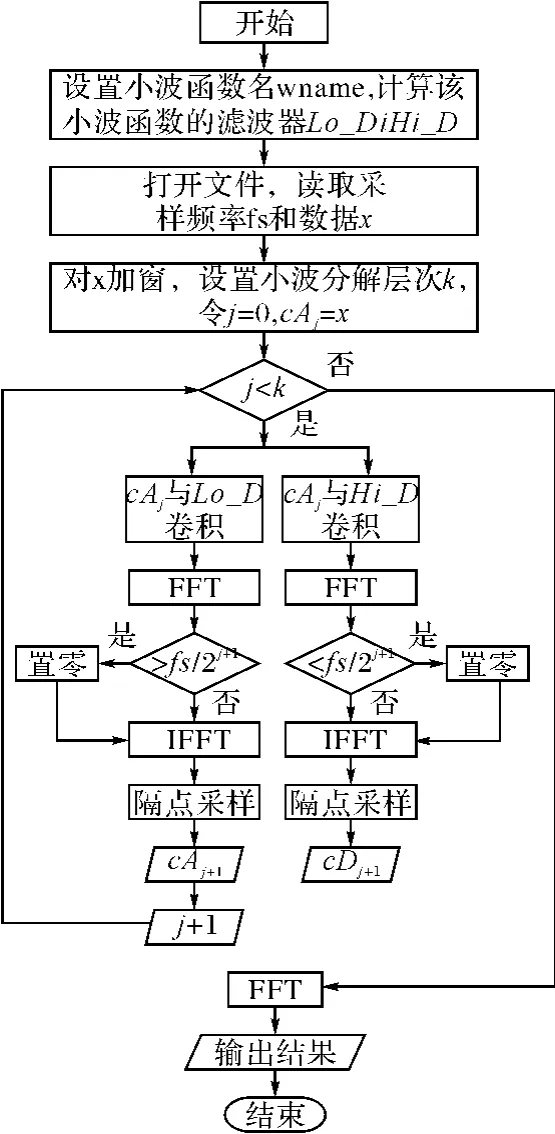
图3 算法流程图
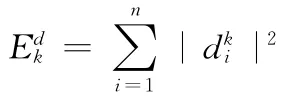
其中n为序列dk的个数。
4)构造特征向量。由于系统出现故障时会对各频带内信号的能量有较大的影响,因此以能量为元素可以构造一个特征向量。把选取的这些频带的能量占总能量的比例作为特征参数并将其组成特征向量,如下式:
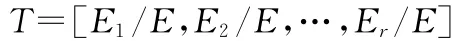
其中E为各频带能量的总和。
5 仿真分析
为验证这一算法的有效性,我们以某一正弦叠加信号s为例来进行分析。图4为该信号的时域图和频谱图,采样频率为800Hz。采用db5小波对该信号进行3尺度的小波分解,从理论上来说,分解的高频部分d1所对应的实际频率为[fs/4,fs/2](fs为采样频率),d2所对的实际频率为[fs/8,fs/4],d3所对的实际频率为[fs/16,fs/8],依次类推,低频部分a1所对应的实际频率为[0,fs/4],a2所对的实际频率为[0,fs/8],a3所对的实际频率为[0,fs/16]。所以应有如下的频率对应关系:d1:200-400Hz,d2:100-200Hz,d3:50-100Hz,a1:0-200Hz,a2:0-100Hz,a3:0-50Hz。
但事实上由于小波的高、低通滤波器不具有理想的截止滤波特性,会产生较为严重的混频现象,从图5和图6可以看出,应用通常的小波分解产生了70Hz、80Hz、110Hz、180Hz的虚假频率成分。而用本文提出的改进算法对该信号进行小波分解后,这些虚假频率成分已经完全被消除了,只剩下45Hz、90Hz、120Hz、130Hz,也即是原始信号在此区间的频率成分。表明该方法在消除混频方面确实是有效的,能够提高故障特征提取的准确性,从而进一步说明了该方法在故障诊断中的实用性。图7为利用该方法进行特征提取所得到的特征向量的直方图。
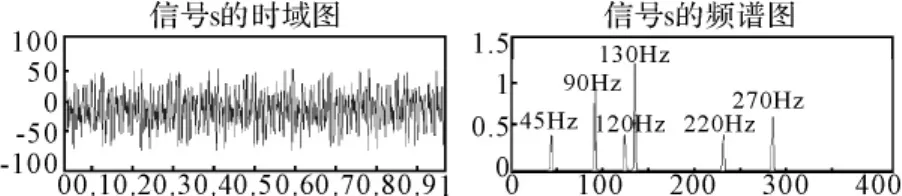
图4 信号s的时域图及频谱图
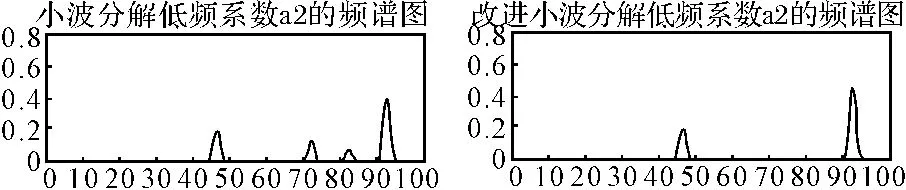
图5 两种算法低频系数的频谱图

图6 两种算法高频系数的频谱图
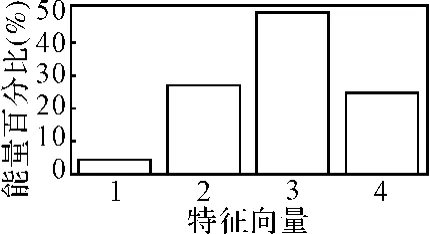
图7 特征向量直方图
6 结语
小波变换具有优良的时频分析特性,适合于提取非平稳信号和时变信号的特征。然而由于小波函数滤波器的截止滤波特性不理想,所以在对信号进行小波分解时会存在严重的混频现象。改进的小波分解算法则从一定程度上消除了这种频率混叠现象,利用这种方法对于提取舰炮齿轮箱的故障特征信息具有重要的现实意义。
[1]史跃东,焦自平.基于BP网络的舰炮齿轮箱故障诊断方法[J].火炮发射与控制学报,2006(1):62-64.
[2]徐长发,李国宽.实用小波方法[M].武汉:华中科技大学出版社,2001.
[3]程正兴.小波分析算法与应用[M].西安:西安交通科技大学出版社,1998.
[4]陈涛,屈梁生,耿中行.小波分析及其在机械诊断中的应用[J].机械工程学报,1997(3):76-79.
[5]李录平,韩守木,黄树红,等.旋转机械故障特征的定性提取[J].华中理工大学学报,1998(1):101-103.
[6]徐科,杨德斌,徐金梧.小波变换在齿轮局部故障诊断中的应用[J].机械工程学报,1999(3):105-107.
[7]张成宝,丁玉兰,吴光强.汽车变速箱齿轮状态识别方法的研究[J].同济大学学报,2000(2):236-240.
[8]陈长征,罗跃纲,张省.基于小波分析的机械故障特征提取研究[J].机械强度,2001(2):161-164.
[9]张德祥,汪萍,吴小培,等.Hilbert-小波变换的齿轮箱故障诊断[J].计算机应用研究,2011(11):4236-4239.
[10]王巧花,邬昌军.小波变换在齿轮故障诊断中的应用[J].煤矿机械,2012(1):272-274.
