小半径城市高架曲线梁桥地震动响应研究
2012-06-05戴公连刘文硕
戴公连,刘文硕,曾 敏
(1.中南大学 土木建筑学院,长沙 410075;2.中国铁道第四勘察设计院,武汉 430063)
现代交通网络中,由于地形、交通等条件的限制以及城市景观的需要[1],曲线梁桥特别是小半径曲线梁桥越来越多地应用于城市道路建设中,尤其在立交桥的匝道设计中应用最广。
在城市立交中,曲线桥主要布置在匝道转弯处,是复杂的非规则空间结构[2],具有弯扭耦合严重的特点,震害最为明显。对于曲线桥的静力特性,国内外已形成有效的计算方法[1],但对于其动力性能,特别是其地震特性的研究目前仍然较少。Chang等[3]运用 Rayleigh-Ritz方法来计算高墩曲线桥梁的振型及地震反应。袁万城等[4]对一座曲线桥进行了线性和非线性空间地震时程反应分析,考虑了行波效应,比较不同支承条件下结构地震反应的差别。聂利英等[5]考虑墩柱非线性及橡胶支座和滑板支座的非线性,同时计入碰撞的影响,完整的对上海莘庄立交桥中的一段曲线桥进行了抗震性能评估。
在2008年的汶川大地震中,曲线梁桥银河一号桥和百花大桥的垮塌使得城市生命线中断,造成难以估计的损失,也反映了曲线桥地震研究的重要性。近年来随着城市建设的大规模展开,曲线桥的设计半径越来越小,其地震性能研究也凸显迫切。本文以武汉新站站前高架一座五跨小半径曲线梁桥为研究对象,研究了合理计算模型的选取,计算了其动力特性,并对影响其地震响应的多个敏感因素进行了分析和探讨。
1 工程概况
新建武汉站站前高架由东西两幅进出站匝道(各十联高架桥)组成,其中西十联为5×25 m预应力混凝土连续梁桥,本联桥设计中心线为直线+圆曲线+直线,两直线夹角近似为90°,曲线半径R=55 m。该桥采用直径2 m的钢筋混凝土圆形桥墩,墩高4.3 m~9.4 m不等,每个桥墩下布置4根桩径1.2 m的钻孔桩。桥型布置及约束方式见图1,标准断面见图2。
2 结构模型探讨及动力特性分析
桥梁结构的动力特性与其地震响应密切相关,选择合理的计算模型计算桥梁的自振频率和振型是进行地震响应分析的基础[6]。此外,小半径曲线桥具有独特的地震特性,在地震力激励下发生弯曲的同时会伴随产生扭转效应。目前,常见的空间计算模型有单根梁模型、板壳模型及普遍用于斜拉桥动力分析的脊梁模型[7-8]。有效合理的动力计算模型,应能够反映曲线桥的空间振动特征,且能体现结构弯扭耦合的特征;同时在保证足够的工程计算精度的前提下,模型应尽可能地简单、易于操作。
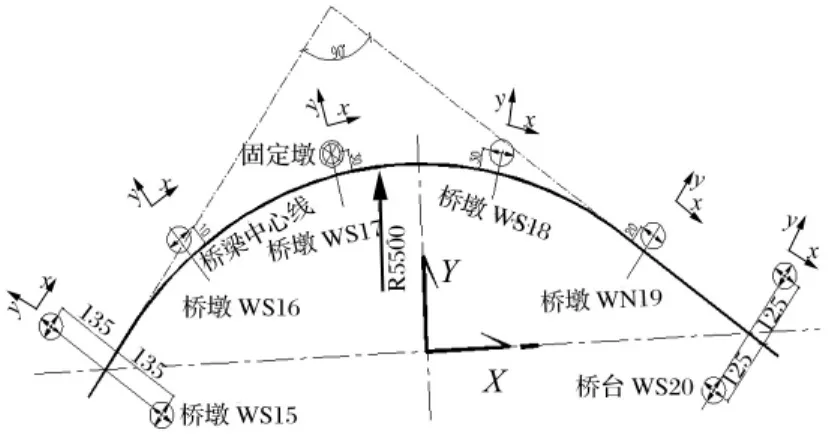
图1 桥型布置及约束方式示意图(单位:cm)Fig.1 Layout of span distribution and constraints(Unit:cm)
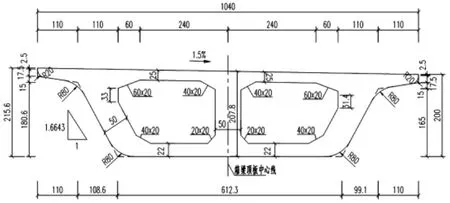
图2 箱梁标准断面图(单位:cm)Fig.2 Typical cross- section(Unit:cm)
2.1 模型介绍
采用有限元软件ANSYS建立该桥的空间模型,选用三种不同的建模方法来模拟结构。为简化比较,三种模型均采用墩底固结,相邻后续结构的影响此处暂不考虑,下文将详细探讨。
模型A:单根梁模型,梁部采用BEAM 188空间直梁单元,节点取箱梁截面形心位置,自重及二恒集中作用在节点上,采用弹性空间直梁单元模拟桥墩,刚性梁单元模拟支座,刚臂单元模拟支座偏心及盖梁。该模型计算单元少,自由度少,计算耗费机时较小。
模型B:板壳单元模型,采用弹性板单元SHELL63划分梁体,BEAM188空间梁单元模拟桥墩,调整箱梁顶板单元的密度以考虑桥面铺装及防撞栏的质量,以便真实模拟实际结构。
模型C:脊梁模型,基本模型与单根梁模型相同,但自重及二恒按内外弧侧相应弧长均集中加载在位于左右各1/2截面质心位置的节点上,两节点通过刚臂与主梁连接[7]。该模型中,可以考虑自重及二恒在桥面的横向分布,主梁不提供质量仅提供刚度。
三种计算模型如图3~图5所示。
图3 单根梁模型Fig.3 Single beam model

图4 板壳单元模型Fig.4 Shell element model

图5 脊梁模型Fig.5 Spine-like beam model
2.2 动力特性比较
计算结果表明,该桥的前4阶振型均为平动或平弯振型,自第五阶开始出现弯扭耦合振型,且频率密集,表明该桥弯扭耦合严重。
比较三种模型下的自振特性,三种模型前10阶振型的出现顺序基本一致,频率计算结果也基本吻合,首阶振型频率相差不足1%。但是,各模型的高阶振型出现不一致,且单根梁模型的前10阶振型中未出现曲线梁计算中出现的扭转振型。在高阶弯扭耦合振型中,脊梁模型与板壳单元的频率误差较小,说明脊梁模型相对单根梁模型而言能较好的考虑质量的分布,有较高的精度。
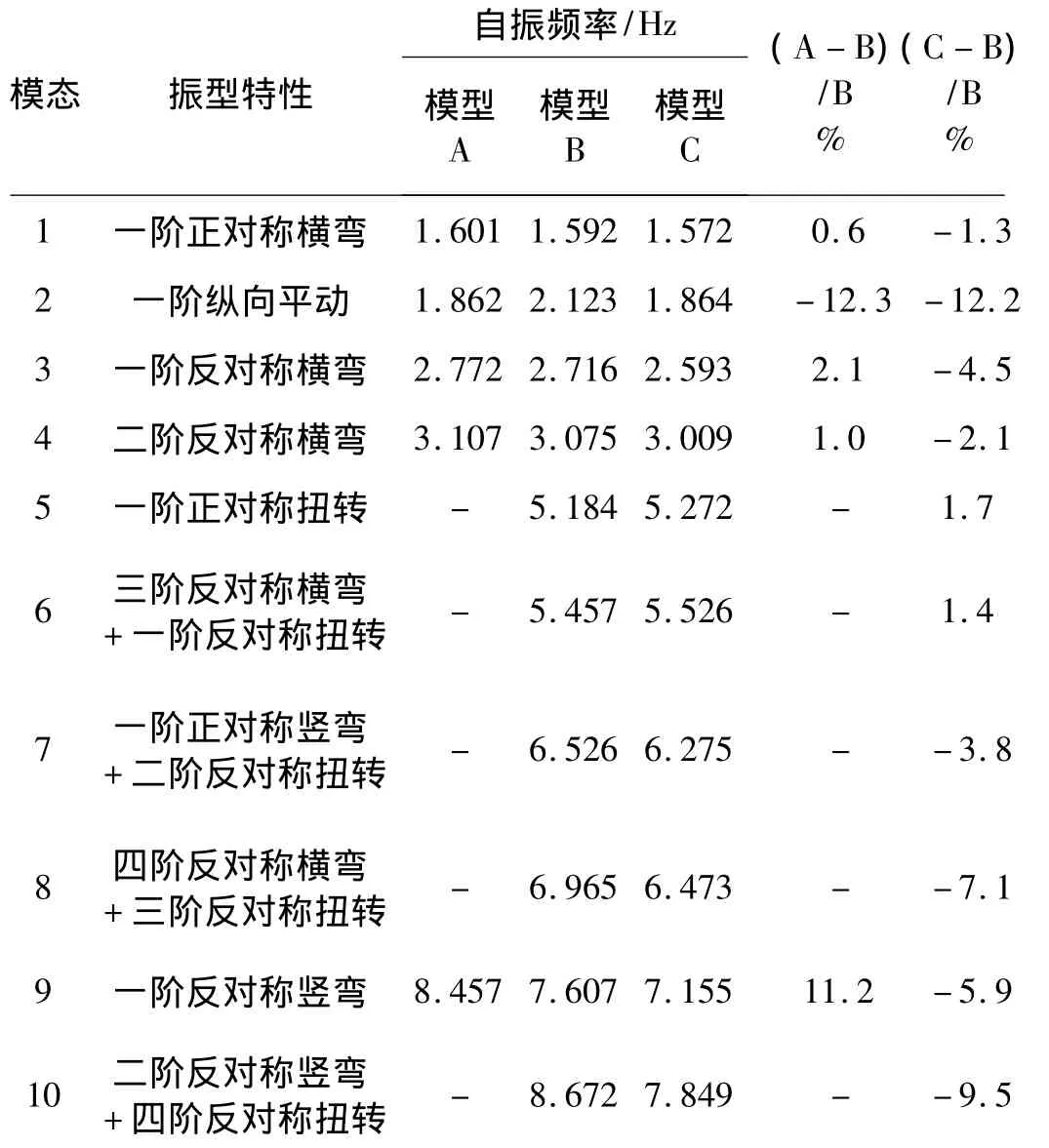
表1 不同模型自振特性对比Tab.1 Natural vibration characteristics of three different models
此外,本文还选用EI Centro波在三个方向(以两端支座中心连线为X轴方向,与之垂直的方向为Y方向,竖向为Z向,见图1)同时输入地震波,对板壳单元模型与脊梁模型进行时程分析比较,计算结果表明2种模型计算得到的梁端位移、端部抗扭支座竖反力、墩底剪力差别较小,最大差值在12%左右。
通过分析对比可知,单根梁无法考虑箱梁质量在横桥方向的分布,不能准确反映小曲率半径曲线梁的弯曲-扭转振动的空间效应;板壳模型适合曲线梁桥的模拟,但建模复杂,单元数目多,计算量大,一般不适合曲线桥的时程分析;而脊梁模型能较好地模拟曲线箱梁的空间振动情况,保证工程计算应有的精度,且计算过程并不复杂,适用于小半径曲线桥的地震响应分析。
3 地震响应敏感因素研究
地震的本质是多维振动,桥梁在地震作用下是复杂的空间振动。研究表明,小半径曲线桥的地震响应与后续结构、桩-土-桥相互作用、桥墩刚度以及支座偏心的设置等多个因素相关,下文采用有效的脊梁模型,基于线性时程分析方法,对上述因素进行研究。
3.1 地震波的选用及调整
本桥设防烈度为7度,水平基本地震加速度峰值为0.10 g(1 g=9.8 m/s2),场地类别为建筑Ⅱ类场地,设计地震分组为第1组,特征周期为0.35 s。由于很难总结出精度高的通用方法来确定地震波,且本桥桥址未作安全评价,为了使研究不失一般性及典型性,选取地震研究中经典的实际地震动加速度记录——1940,El Centro Site波进行计算,按一致激励采用三向地震波同时输入,三向加速度最大值按 1∶0.85∶0.65(水平1∶水平2∶竖向)的比例进行调整[10]。
由于曲线弯梁桥的地震响应分析中存在地震动最不利输入方向的问题[11-12],经过笔者多次试算,对于本桥而言,基本可将曲线梁两端为端点的弦线方向(即X方向)以及与之垂直的方向(即Y方向),作为地震动主方向的最不利输入方向,见图1所示。下文在讨论各影响因素时,均采用Rayleigh阻尼,不计墩帽挡块等的碰撞作用。
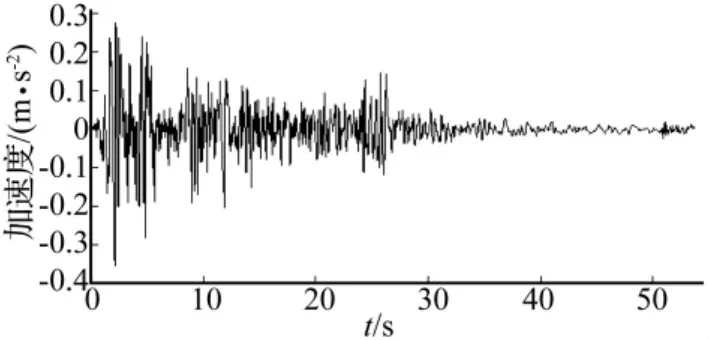
图6 地震加速度时程(El Centro Site)Fig.6 Acceleration time history under earthquake
3.2 后续结构的影响
高架桥各联间由于伸缩缝等联系的存在而具有较强的整体耦联性,因此各联的地震反应并不是独立的,相邻后继结构对所分析桥梁的地震反应有较大影响[12-13]。利用ANSYS软件建立西十联的脊梁模型,并将其后续结构建立在整体模型中,由于西十联一侧与既有市政道路相接,因此只需建立与之相联的西九联,后续结构始终按墩底固结处理。同时,为模拟由于相邻联非同向振动可能导致的伸缩处碰撞,伸缩缝采用ANSYS自带的接触单元CONTA178模拟,接触单元的非线性力-位移关系如下。
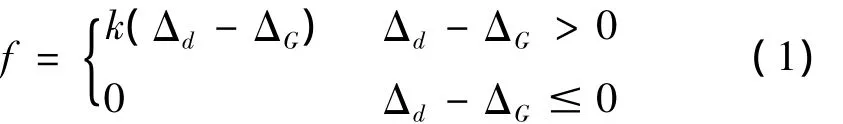
式中:ΔG为伸缩缝初始间隙;Δd为地震作用下伸缩缝处相邻梁体的相对位移;k为接触刚度,取梁体的轴向刚度[14-15]。后续结构对结构动力特性的影响见表2,EI Centro波作用下时程分析计算结果见图7。
从表2可以看出,考虑后续结构时,前几阶模态基本一致,共有振型差别很小,相同振型频率相差小,均小于3%。后续结构相当于一个弹性抗扭约束,通过交接墩盖梁对曲线桥施加扭矩,对靠近扭转中心的中间墩位置影响较小,而对抗扭刚度较大的两端影响较大。

表2 考虑后续结构时的动力特性Tab.2 Structural dynamic characteristics considering the adjacent structures
从图7后续结构对结构时程反应峰值的影响可以看出:考虑后续结构时,结构支反力和墩底切向弯矩均呈交替变化,两端支座支反力变化明显,交接墩墩底切向弯矩变化较为突出。此外,两端支座顶部梁体顺桥向位移有所增大,而横桥向位移有所减小。
3.3 桩-土-桥相互作用的影响
土与结构的相互作用可以使结构体系变柔增大结构周期,也可以改变结构的地震动输入。文中按假定“土弹簧法”讨论桩-土-桥相互作用对结构的动力特性及时程响应分析结果的影响,将桩基模拟为弹性地基上的连续梁,按m法考虑桩基的弹性刚度,将桩群周围的土简化为弹簧,按照等刚度原则计算土弹簧的等效刚度[15]。模型如图8所示。

图7 后续结构对结构时程反应峰值的影响Fig.7 The influence of adjacent structure on the peak value of the time history response
图8 考虑桩-土-桥作用的整体有限元模型Fig.8 The whole finite element model considering the pile-soil-bridge interaction
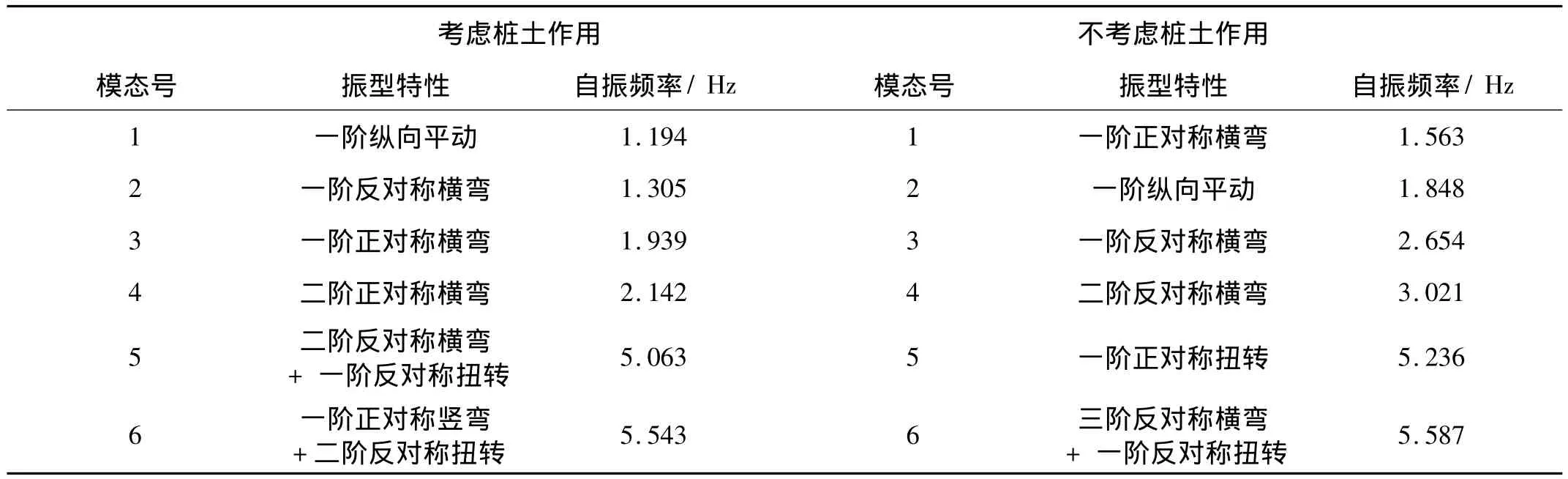
表3 桩-土-桥作用对曲线桥动力特性的影响Tab.3 The pile-soil-bridge interaction’s influence on the dynamic characteristics of the curved bridge
由表3可知,考虑桩土作用时结构变柔,第一阶自振频率降幅达24%,且振型出现的先后次序有所变化,一阶纵向平动振型提前出现。
通过对比考虑桩-土-桥作用前后的时程分析结果可以看出,桩-土-桥相互作用对小跨度曲线高架桥的地震反应影响很大,其影响主要体现在以下几个方面:
(1)交接墩处支反力增大,桥台支反力减小,两端支座支反力变化明显,墩台处相对较小,主要是因为引入桩基刚度后,结构沿纵向的刚度分配发生改变。
(2)墩底切向弯矩均明显减小,径向弯矩只有固定墩(17#)显著减小,幅值达62%。
(3)端支座顶梁体横桥向位移均有所增大且桥台处位移增大最多,主要是由于考虑桩-土-桥共同作用后,桥台刚度减小的比例比桥墩大;而端支座顶梁体顺桥向位移在交接墩处减小,桥台处增大。
(4)端支座底墩台顺桥向位移随刚度整体降低,位移均显著增大。
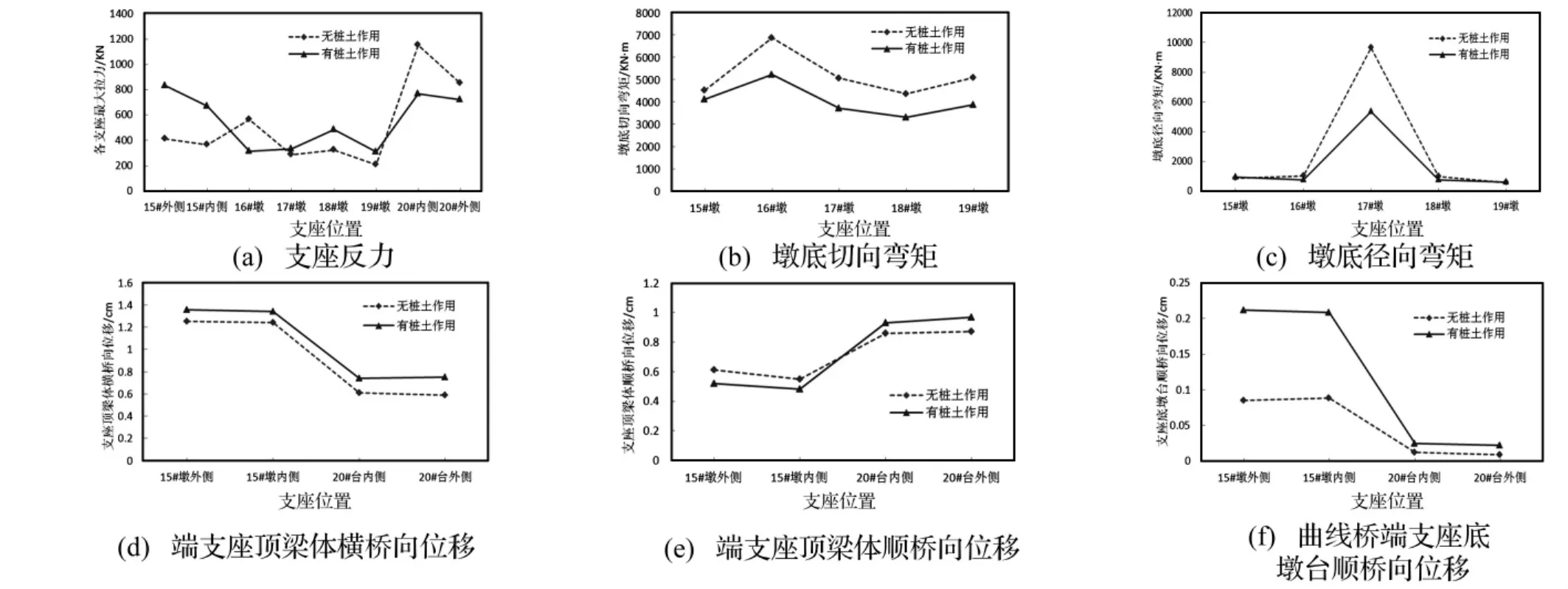
图9 桩-土-桥相互作用对结构时程反应峰值的影响Fig.9 The influence of pile-soil-structure interaction on the peak value of the time history response
3.4 桥墩刚度
在强震作用下,上部结构因自身强度破坏而失效的情况较为少见,而因桥墩破坏倒塌或失效的情况较为常见。为讨论桥墩刚度对小半径曲线桥地震响应的影响,保持桥墩截面尺寸不变,采用整体变化桥墩及桥台高度的办法,在3.3节模型的基础上,在三向地震波时程作用下,比较五种不同墩高对桥梁自振特性和地震响应的影响。
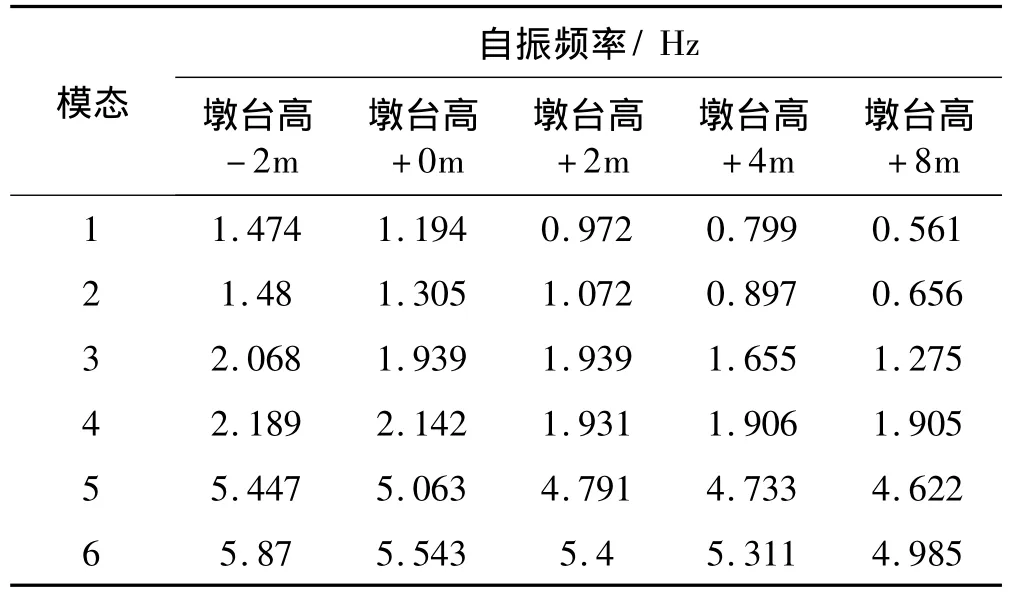
表4 墩台高度对自振特性的影响Tab.4 The influence of pier’s height on the natural vibration characteristics
从表4可以看出,随着墩高的增加,各阶频率均呈降低趋势,前两阶基本上呈线性降低趋势。
3.5 支座偏心
在曲线桥的支座布置中,经常采用支座偏心的方式改变恒载下主梁扭矩的分布,以改善梁端抗扭支座的受力情况。但支座偏心可能使得曲线桥在地震动作用下主梁扭转力更大,为探究支座偏心对小半径曲线桥地震响应的影响,以原设计为基本,基于3.3节的有限元模型,共选取5种偏心情况进行计算。表5和图11中分别示出了不同支座偏心情况对该联桥自振特性及结构地震响应的影响。
从表5中的频率计算结果可以看出,各阶频率相差甚少,表明结构自振频率基本不随偏心变化。选用EI Centro波进行时程分析,从图11可以看出,内力及位移随偏心的增大变化十分微小,说明支座偏心只影响结构的内力分配,对刚度及动力响应的影响可以忽略。
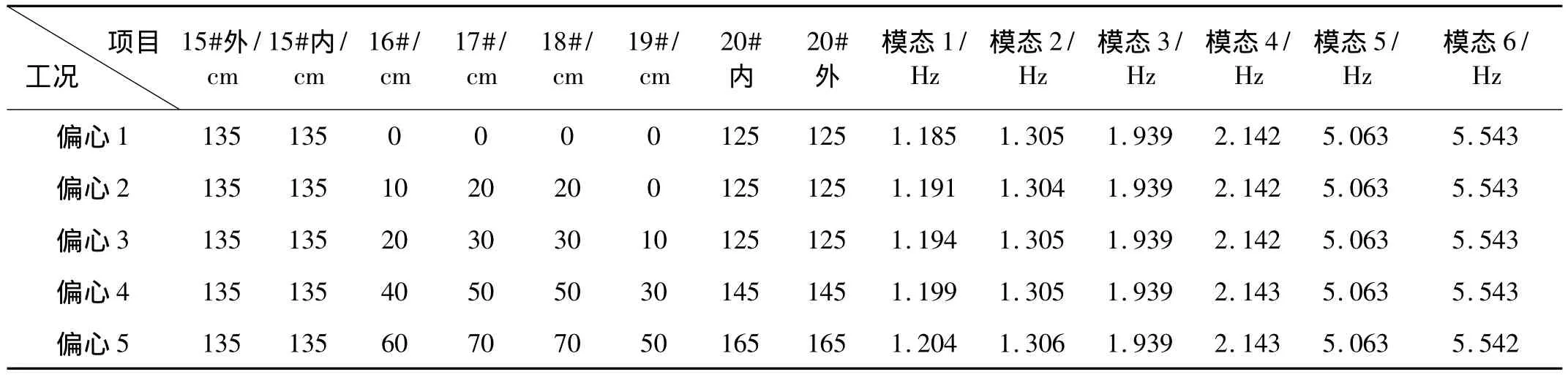
表5 支座偏心工况及自振特性汇总表Tab.5 Structural natural vibration characteristics under different conditions of bearing eccentricity
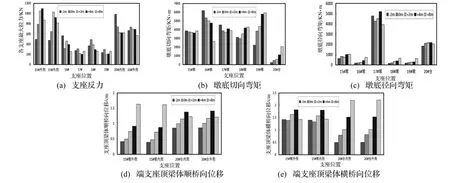
图10 墩台高度对曲线桥地震反应的影响Fig.10 The influence of pile and abutment’s height on the structural seismic responses of curved bridge

图11 支座偏心对曲线桥地震反应的影响Fig.11 The influence of bearing eccentricity on the structural seismic responses of curved bridge
4 结论
(1)脊梁模型建模简单方便,计算量相对较小,且能保证计算的精确度,适用于小半径曲线梁桥上部结构动力分析的的模拟。
(2)后续结构对曲线桥地震反应各项响应均有一定程度的影响,特别是对于扭转敏感的支反力影响很大,结构分析时应合理考虑后续结构。
(3)桩-土-桥相互作用对矮墩小跨度的曲线高架桥地震反应具有较大影响,特别是对径向弯矩及支座底墩台顺桥向位移的影响较为突出。
(4)曲线桥地震反应对桥墩高度变化十分敏感,且没有统一的规律性,设计时应选择合理墩高。
(5)支座偏心只影响曲线桥的成桥内力分配,对其刚度及动力响应的影响可以忽略。
(6)碰撞作用对结构的地震反应有一定影响,曲线桥地震响应下的碰撞分析有待进一步的研究。
[1]朱东生,刘世忠,虞庐松.曲线桥地震反应研究[J].中国公路学报,2002,15(3):42 -48.
[2]魏双科,李鸿晶,罗寒松,等.立交桥曲线箱梁动力分析模型[J].地震工程与工程振动,2006,26(4):168-174.
[3]Chang P C,Heins C P.Seismic study of curved bridges using the rayleigh - ritzmethod [J].Computers and Structures,1985,21(6):1095-1104.
[4]袁万城,王玉贵,杨玉民.曲线梁桥空间地震反应分析[A].第十二届全国桥梁学术会议论文集[C].上海:同济大学出版社,1996,585-590.
[5]聂利英,李建中,胡世德,等.曲线梁桥非线性分析及抗震性能评估[J].同济大学学报,2004,32(10):1360-1364.
[6]宋旭明,戴公连,曾庆元.自锚式悬索桥地震响应及减震控制分析[J].中南大学学报(自然科学版),2009,40(4):1079-1085.
[7]魏双科.曲线梁桥的固有振动特性及地震反应分析[D].南京:南京工业大学,2006.
[8]李国豪,石 洞,Heins C P.曲梁桥地震分析的有限单元法[J].同济大学学报(自然科学版),1984,23(1):1 -21.
[9]范立础.桥梁抗震[M].上海:同济大学出版社,1997.
[10]中华人民共和国交通部,JTJ004-89.公路工程抗震设计规范[S].北京:人民交通出版社,1990.
[11]全 伟,李宏男.曲线桥多维地震时程分析主方向研究[J].振动与冲击,2008,27(8):20 -24.
[12]曾 敏.小半径曲线梁桥地震响应分析及减隔震研究[D].长沙:中南大学土木建筑学院,2009.
[13]范立础,李建中,王君杰.高架桥梁抗震设计[M].北京:人民交通出版社,2001.
[14]Malhotra P K.Dynamics of seismic pounding at expansion joints of concrete bridges[J].Journal of Engineering Mechanics,1998,124(7):794 -802.
[15]王军文,张运波,李建中,等.地震动行波效应对连续梁桥纵向地震碰撞反应的影响[J].工程力学,2007,24(11):100-105.
