无理式系统的主共振分岔分析

刘延彬，陈予恕，曹庆杰

(哈尔滨工业大学 航天学院137信箱，哈尔滨 150001)

在过去的一个世纪中，非线性动力学取得了巨大的成就［1］。传统的非线性动力学解析方法分析的研究对象为多项式系统，对于含有无理式的非线性微分方程，均将无理式展开成多项式形式。多项式仅仅是无理式的一种局部近似，当研究非线性系统的非局部行为时，多项式近似逼近无理式会带来偏差，甚至得到的一些性质根本不是原系统的性质。目前人们对无理式系统的理解仍然具有很大的偏差，不能满足研究和工程应用的需要，而工程中存在大量的无理式系统，例如:油膜力，非线性气动力等［2－4］，为此，研究无理式系统的性质是重要，而且是十分必要的。曹庆杰等［2］研究了SD振子，得到了SD振子的动力学特性，该工作是比较系统的研究无理式系统的工作。虽然有一些工作开始关注无理式系统，但是由于无理式系统求解是十分困难的，大部分工作均是基于数值模拟，不能满足研究和应用的需要。

本文采用平均法、奇异性理论［5－6］及吸引盆研究了一类无理式系统的性质，该类无理式系统是由弹簧－连杆机构构成，虽然弹簧是线性的，由于几何特征，弹簧表现为非线性的恢复力。该系统依赖于参数 α，当 α＞0时，系统为正的非线性刚度，表现出硬特性;当α=0时，系统为线性系统;当α＜0时，系统为负的非线性刚度，表现出软特性。该系统刻画了系统从线性系统到非线性系统及从负刚度系统到正刚度系统的变化过程，是一类典型的非线性动力学方程。

1 系统方程的建立及分析

本文研究弹簧－连杆机构，机构如图1所示:

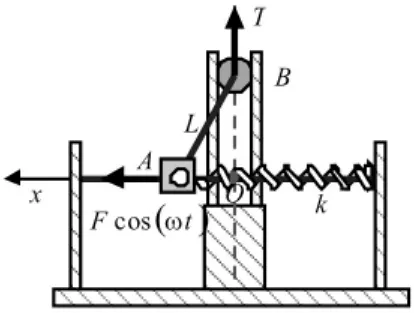
图1 连杆模型Fig.1 The model of linkage mechanism

O点为锁机构，当小球运动到B运动到 O点，系统锁住，不再运动。忽略连杆及滑道中小球的B质量。忽略小球B所受的摩擦力，设滑块A的质量为 m，取 O点为平衡点，以x方向为正方向，可以建立运动方程如下:

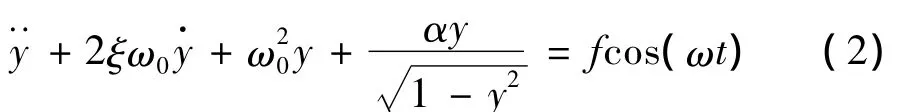
当α＞0，即T＞0时，方程(2)为正的非线性刚度，表现出硬特性;当α=0，即T=0时，方程(2)为线性系统;当α＜0，T＜0时，方程(2)为负的非线性刚度，表现出软特性。因此该系统刻画了系统从线性系统到非线性系统及从负刚度系统到正刚度系统的变化过程，是一类典型的非线性动力学方程。

2 方程的主共振分析

当α=0时，方程(2)为线性系统，本文只研究α≠0时的情况。当系统产生共振时，满足以下关系式:

δ为调谐参数。设方程(2)的解为:

则方程(2)成为:

由平均法可得:

系统的幅频曲线方程为:

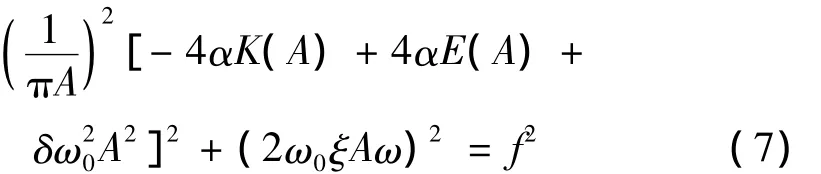
其中K和E为完全椭圆函数。由式(3)和方程(7)可得:

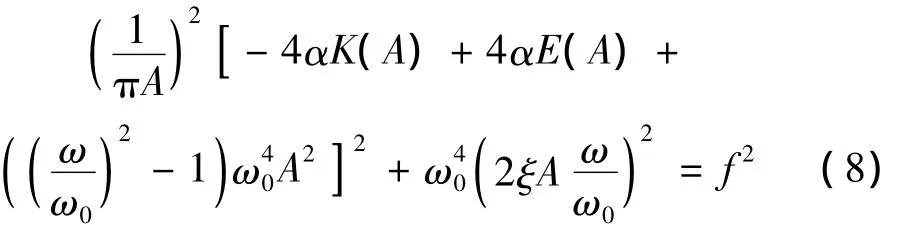
当 ω0=1，α =0.1，f=0.5，ξ不同时，系统的幅频曲线如图2(a)所示;.当 ω0=1，f=0.5，ξ=0.1，α 不同时，系统的幅频曲线如图2(b)所示，当ω0=1，ξ=0.1，α=1，f不同时，系统的幅频曲线如图2(c)所示。

图2 系统的幅频曲线Fig.2 The curves of amplitude and frequency

图2(a)、图2(b)和图2(c)所示系统的幅频曲线与Duffing方程的幅频曲线类似［1］，区别在于:① 图2(b)和图2(c)显示出在一定的参数下，系统不存在周期解，这种现象对应实际物理系统中的锁死现象;②系统主共振时，系统的振动幅值不会超过1。③ 在图2(b)和图2(c)中，有的曲线不闭合，而Duffing方程的幅频曲线均是闭合的。为了进一步弄清这些规律，我们利用奇异性理论的方法对振幅方程进行分类研究。

3 奇异性分析

选ω为分岔参数，选α，f和ξ为开折参数，设函数H(A，ω)为:

因为0＜A＜1，完全椭圆函数可以展开成泰勒级数。

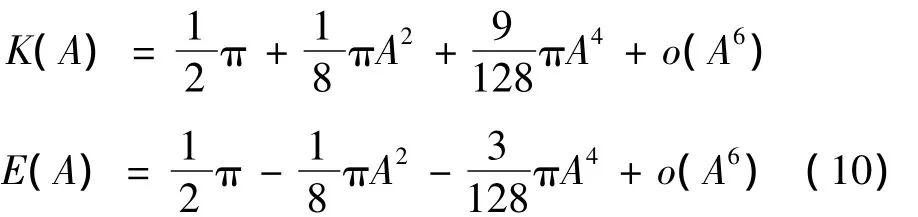
设:

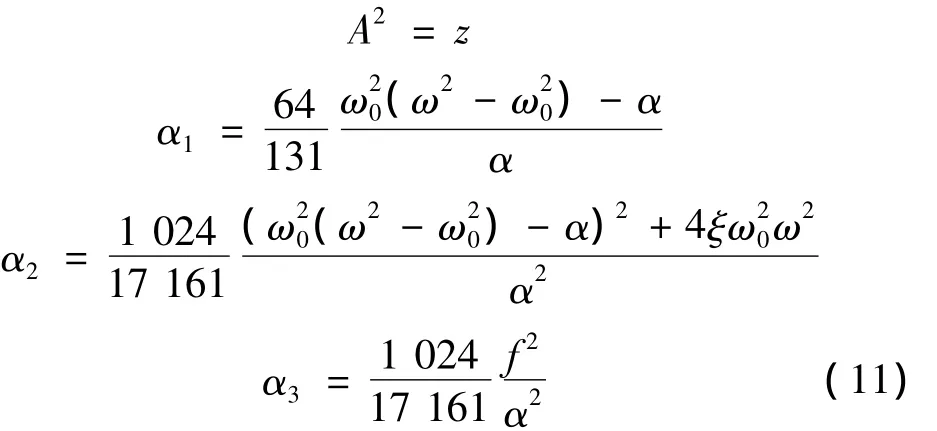
则方程(9)可以写为:

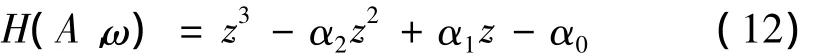
由方程(11)，方程(12)可得:

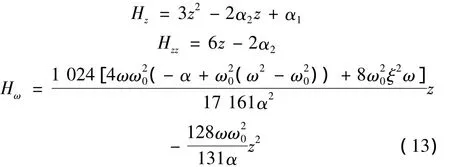
其中:Hz、Hzz、Hω代表对 z、ω 的导数。令的转迁集为:

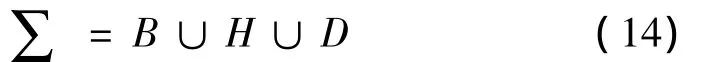
且B集为:H=Hz=Hω=0，H 集为:H=Hz=Hzz=0，所以:

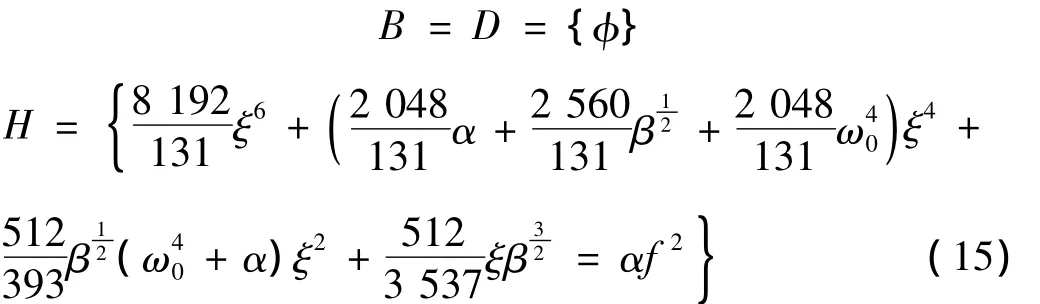
B、H和D分别为分岔集、滞后集和双极限点集。转迁集在参数空间(f，a，ξ)如图3所示。

图3所示的转迁集曲面过于复杂，不利于直观的对参数空间进行分类，为此，我们采用固定 ξ，以参数f和α划分参数空间，以便进一步研究系统的分岔特性。

当 ξ=0.01 时，系统的区间划分如图4(a)所示。当ξ=0.1时，参数区间划分为如图4(b)所示。

图3 转迁集曲面Fig.3 The curved surfaces of transition set

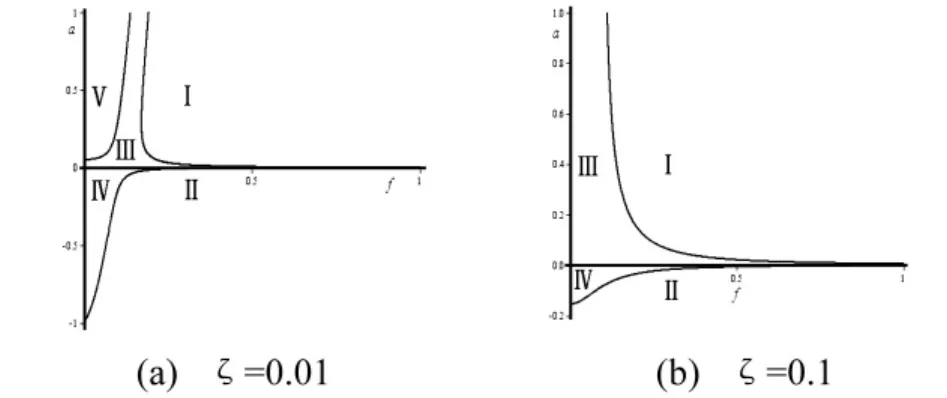
图4 转迁集Fig.4 Transition set

当ξ=0.01时，转迁集将参数区间分为五个区域，各个参数区间的幅频曲线如图6所示。

由图5可以看出，当ξ=0.01时，系统的幅频曲线共有五种形式，其中图5(a)、图5(b)、图5(c)和图5(d)的幅频曲线均是不闭合的，这是无理式系统的特点，在多项式Duffing方程中是不具备的。

当ξ=0.1，转迁集将参数区间分为四个区域，各个参数区间的幅频曲线如图7所示。

图5 ξ=0.01时，系统分岔图Fig.5 The bifurcation diagrams，when ξ=0.01

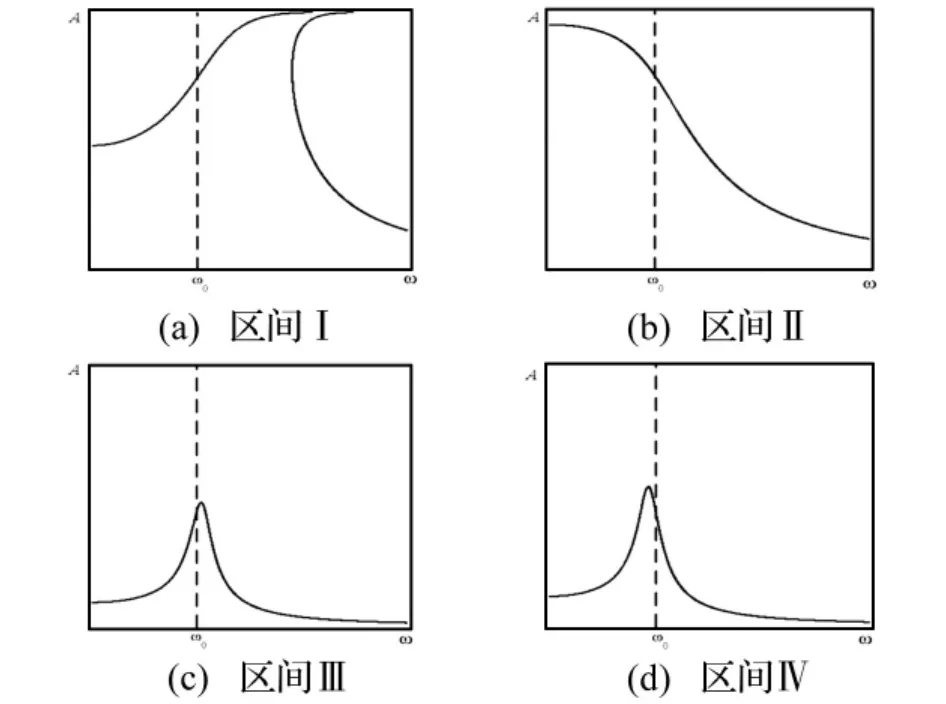
图6 ξ=0.1时，系统分岔图Fig 6 The bifurcation diagrams，when ξ=0.1

由图6可以看出，当ξ=0.1时，系统的幅频曲线共有四种形式，其中图6(a)、图6(b)和图5(a)、图5(b)是一样的;但是增加了两种拓扑结构，6－c和6－d。6－c和6－d的幅频曲线特性在Duffing方程中也是存在的。

4 系统的吸引盆分析

在多项式系统中，系统的任何初值都会收敛到相应的周期解上，由于方程(2)是无理式系统，并不是所有的初值条件都能收敛到周期解，这也是无理式系统不同于多项式系统的地方，故有必要研究系统的吸引盆。在以下的计算中，取 ξ=0.01，ω0=1。当 α =0.2，ω =1.5，f不同时，得到图7。.当 α =2，ω =2，f不同时，得到图8。在图7中，系统只有一个周期解，其中P为吸引域，可以看出，当f增大时，系统的吸引域减小。在图8中，系统有两个个周期解，其中P、Q为吸引域，可以看出，当f增大时，系统的两个吸引域均减小，且随着 f增大，吸引域Q消失，吸引域P进一步减小。

图7 当α=0.2，ω=1时，系统的吸引域Fig.7 The basin of attraction when α =0.2

5 结论

图8 当α=2，ω=2时，系统的吸引域Fig.8 The basin of attraction when α =2，ω =2

本文所研究的无理系统刻画了振动系统的演化过程，当外力T从小到大改变时，系统从弱的非线性刚度到强的非线性刚度转化;当外力T=0时，系统从非线性系统转换成线性系统;当从T负到正改变时，系统从负的非线性刚度系统转换成正的非线性刚度系统。研究结果表明:

(1)无理式系统的特性有别于多项式系统，不能完全由多项式系统代替。

(2)当阻尼参数不同时，系统的幅频曲线的拓扑结构会不同。

(3)在一定的条件下，无理式系统不存在周期解。

(4)在其他参数不动时，随着f的增大，吸引域减小。

［1］陈予恕.非线性振动系统的分岔和浑沌理论［M］.北京:高等教育出版社，1993.

［2］Cao Q，Wiercigroch M，Pavlovskaia E E，et al.An archetypal oscillator for smooth and discontinuousdynamics，Phys.Rev.E 74(2006)046218.

［3］Cao Q，Wiercigroch M，Pavlovskaia E E，et al.Piecewise linear approach to an archetypal oscillator forsmooth and discontinuous dynamics， Philos. Trans. R. Soc. A 366(1865)(2008)635－652.

［4］曹庆杰，Wiercigroch M，Pavlovskaia E E，等.SD振子，SD吸引子及其应用［J］.振动工程学报2007，5.

［5］Golubitsky M，Schaeffer D G.Singularities and groups in bifurcation theory［M］.New York，Berlin，Heidelberg，Tokyo:Springer-Verlag，1984.

［6］陆启韶.常微分方程的定性方法和分叉［M］.北京:北京航空航天大学出版社，1989.