混凝土柱单轴动态抗压特性的应变率效应研究

邹笃建，刘铁军，滕 军，严桂兰

(哈尔滨工业大学 深圳研究生院，深圳 518055)

混凝土材料是典型的率敏感材料，不同应变率下其强度、延性和破坏模式明显改变［1－2］。土木工程中的各种混凝土结构除了承受静荷载外，不可避免地会遭遇到动荷载的作用。而且一些动荷载例如地震作用、台风、海啸等并不是时刻作用在结构上，但它们对结构的破坏性及不可预知性，使其成为控制结构设计的重要因素。针对一定的应变率范围来彻底研究材料的本构关系和破坏机理是非常必要的。

欧洲混凝土协会CEB［3］在总结多数试验成果的基础上，规定了一个准静态应变率，推荐了不同动态应变率下混凝土材料的抗压强度、峰值应变、弹性模量相对准静态应变率下的变化系数。一般认为当混凝土结构存在动力荷载作用时，可以将材料的抗压强度设计值提高25% ～30%，而当结构遭受冲击荷载时(应变率大约为10 s－1)混凝土材料的抗压强度可以提高85% ～100%［4－5］。应变率效应对于混凝土初始弹性模量和峰值应变的影响一直存在争议，Bischoff［6］汇总了前人的试验结果并对其进行了深入的分析。国内的学者闫东明、肖诗云［7－12］进行了大量的混凝土试件的动态试验，他们的研究进一步拓展了混凝土材料动态试验的深度和广度。

由于混凝土本身的离散性，以及试验设备和测量设备的不同，不同研究者所得到的试验结论相差较大甚至互相矛盾，所以对于混凝土材料的本构关系研究，还继续需要新的更多的试验去验证。混凝土材料的动力试验要比静力试验复杂的多，进而影响试验结果的因素也非常多。在分析试验结果的过程中，必须合理的考虑这些影响试验结果的因素，其中包括惯性效应、试件尺寸、应力和应变沿试件纵向的不均匀性、应力波效应以及在高应变率范围内一维波理论的各种限制。对于本文中的试验而讲，在试验过程中，考虑了试验机刚度、惯性效应、应力应变的不均匀性对试验结果的影响。

1 试验

1.1 试验设备和试件

本试验采用 Wawtest液压试验机，最大负荷为5000 kN。在试验过程中需要采集时间、试验力、位移等数据，试验力通过短柱顶端的力传感器测出，位移通过自己加工的引伸计测出，测量标距为300mm，试验设备详图如图1所示。试件的尺寸为150×450mm的圆柱体。混凝土的配合比为胶凝材料总量(水泥和粉煤灰):水:石子:砂子 =1∶0.47∶3.11∶2.19，其中粉煤灰掺量为水泥的21%，另外高效减水剂用量为水泥用量的2.66%，水泥采用P.O42.5R号广东梅州塔牌水泥，骨料为碎石，最大粒径25mm，砂子为河砂。试件用PVC管浇筑成型，在振动台上振捣密实，试件浇筑成型一天后拆模，在养护室恒温恒湿的条件下养护1个月后，取出在室温下养护5个月后进行抗压性能试验。

图1 试验设备详图Fig.1 Details of testing machine

1.2 试验方案

试验主要研究混凝土在地震荷载作用下的动态特性，考虑到结构在地震荷载作用下响应的应变率在10－4/s～10－2/s左右，所以试验的应变率主要分为10－5/s、10－4/s、10－3/s、10－2/s 四 个 数 量 级，并 取10－5/s为准静态应变率。由于混凝土是脆性材料，在普通试验机上进行抗压试验时，超过最大应力(即混凝土抗压强度)后试件立即崩碎。所得的应力应变下降段曲线没有规律，峰值应力处的应变值也因不同的试验机而有很大的差异。Whitney指出，试件的突然破坏是由于试验机本身的刚度不足造成的，试验机在加载过程中，存储了很大的弹性变形能，当试件达到最大承载力后，试验机因荷载减小而迅速的释放能量，对试件施加较大的附加应变而引起急速的破坏。所以在试验中配置了两个刚性元件置于试件两侧，与试件共同受力，以防止试件在超过最大承载力后由于试验机的回弹而使试件突然破坏，试验装置见图1。配置了刚性辅助设备后，柱试件和钢管柱的刚度和对试验机作用在试件上的位移加载速率有较大影响，所以需要通过式(1)来对试件的位移加载速率进行调整。惯性效应随着加载速率的提高对试验结果的影响加大，可以通过式(2)来计算试验中惯性效应对试验结果的影响有多大，通过把压力传感器放在柱试件上端(试验机的油泵在试件下端，试件的下端是加载端)能弱化惯性效应的影响。

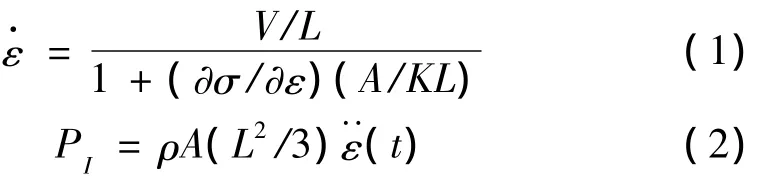
式中:V为试验机加载速率;L为试件长度;A为试件截面积;∂σ/∂ε为试验材料某应力状态的切线模量;K为试验机刚度;PI为等效惯性力;ρ为试件材料的密度。

(1)试验前的准备工作

试验前，先要对荷载传感器、引伸计进行标定，建立标定文件，对加载系统进行调试。

(2)试件处理及测点布置

在试件圆周四等分点处粘贴引伸计以测量竖向应变。

(3)试件安装

按照设备详图分别安装好荷载传感器、试件，初步对试件进行几何对中，首先调整试件位置，使其基本位于设备的几何中心;然后以准静态应变率对柱试件进行3～5次预压，预压荷载值取柱试件静态抗压强度的30%。预压后安装好引伸计，以不同的恒定的位移加载速率对柱试件进行轴心抗压性能试验。

2 结果分析

由于混凝土动力试验受到试验设备、试验技术及试件离散性等多方面的影响，试验的成功率较静力试验偏低，而且由于高应变率时，对试验机的要求比较高，应变率为10－2/s的抗压试验并没有加刚性辅助设备。下面结果分析中的抗压强度、弹性模量、峰值应变的值为剔除异常数据点后，柱试件的平均值。

2.1 应力－应变曲线

图2为混凝土柱试件在不同应变率下的应力－应变全曲线，从图中可以看出这些曲线都基本反映了混凝土的受压特性。试件在受载初期基本上处于线弹性阶段，应力－应变曲线呈线性变化;随着应力的增加，当应力达到一定值时，试件内部的初始裂纹开始发展或出现新的裂缝，应力－应变曲线呈非线性变化;随着应变率的增加，加大了初始裂缝发展和新裂缝发展的应力水平，延长了本构关系的弹性段。

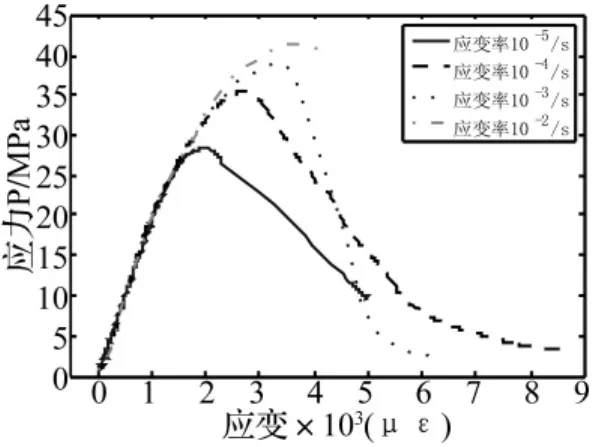
图2 不同应变率下应力－应变关系曲线Fig.2 Relationship of strain rate and constitutive relation

2.2 试验影响因素分析

2.2.1 试验机刚度

利用式(1)可讨论试验机的刚度对混凝土试件应变率的影响。当在试验中配置了刚性元件以后，式(1)可被修正为式(3):

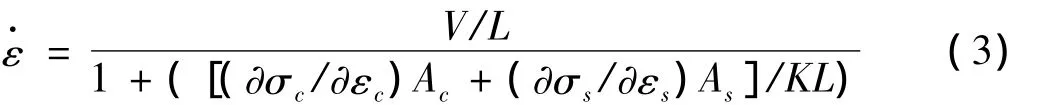
其中:∂σs/∂εs为刚性元件某应力状态下的切线模量;As为刚性元件截面积;∂σc/∂εc为混凝土柱试件某应力状态下的切线模量;Ac为混凝土柱试件截面积。

Wawtest液压试验机在考虑液压油压缩性情况下，取其刚度为1000 k N/mm。对试验中使用的刚性元件做单轴抗压试验，可以发现刚性元件在0－6000微应变范围内，切线模量基本不变。式(3)中唯一的未知部分就是混凝土柱试件在任意应力状态下的切线模量。为方便对混凝土某应力状态下的切线模量进行讨论，利用清华大学过镇海提出的双参数模型对试验曲线进行拟合，并对拟合后的曲线求导，进而可以方便的得到任意应力状态下应力－应变曲线的切线模量。过镇海提出的双参数模型具体表达式为:

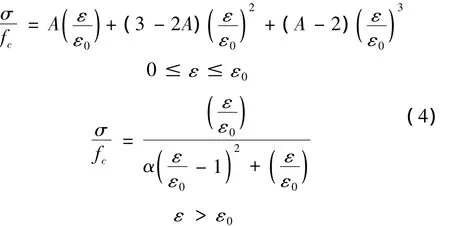
本次试验以及以往的试验都证明在不同应变率下，混凝土应力－应变曲线在形状上是相似的。进而完全可以利用现有的静态本构模型，通过调整参数来发展成为不同应变率下的动态本构模型，一条受压应力－应变曲线的控制点在于弹性模量、抗压强度和峰值应变，这三个物理量确定了，不同模型的应力－应变曲线基本上就可以确定了。对于过镇海提出的静态本构模型，有两个未知数A和α。A是初始弹性模量和峰值割线模量的比值，α是调整曲线下降段形状的参数。通过汇总不同学者的动态试验数据可以拟合出参数A和α的表达式，进而可以实现比较合理的不同应变率下的动态本构模型。以本文试验应变率10－4/s情况下的试验曲线为例进行拟合，得到应力－应变曲线的表达式如式(5)所示。对式(5)进行求导，可得到曲线在任意应力状态下的切线模量。

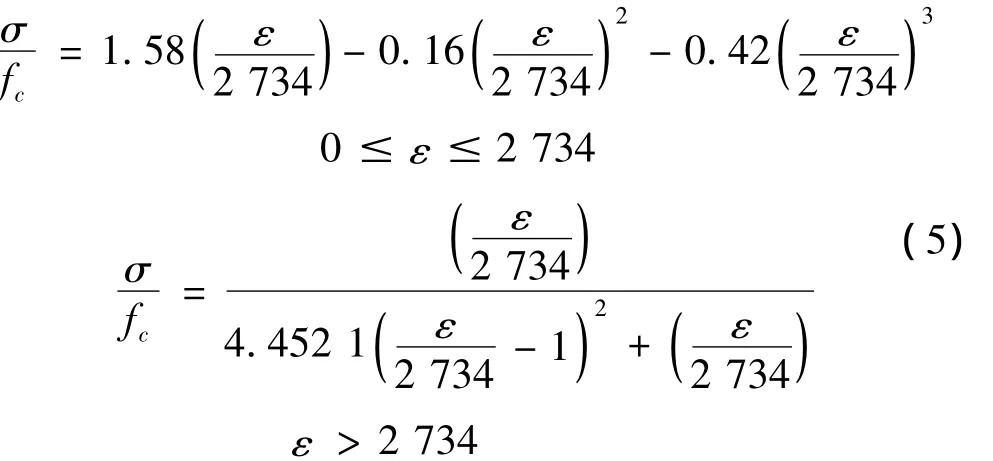
试验过程中是否使用刚性元件对试件的应变率范围影响很大，利用10－4/s下应力应变关系曲线的切线模量，通过式(3)来讨论应变率的变化范围。不使用刚性元件时，试件应变率的变化范围为［0.55～2.20］·(V/L);使用刚性元件后，试件应变率的变化范围为［0.1214 ～0.1452］(V/L)。由此说明附加刚性元件以后，在单轴抗压试验中，试件应变率范围的稳定性有了比较好的改善，但是对于同一试件应变率，需要较大的位移加载速率来实现。对其它几种应变率情况下的曲线经过分析后，本次单轴抗压试验的位移加载速率和试件的应变率范围汇总如下:

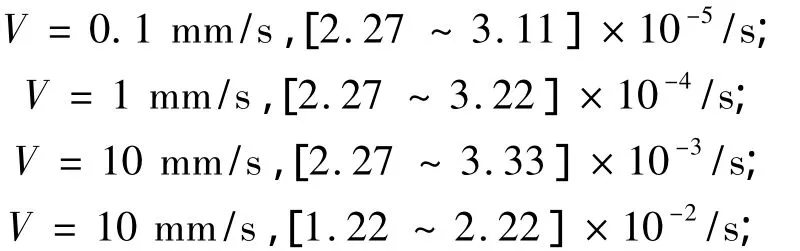
(无辅助刚性元件、没有讨论应力－应变曲线下降段)

2.2.2 惯性影响

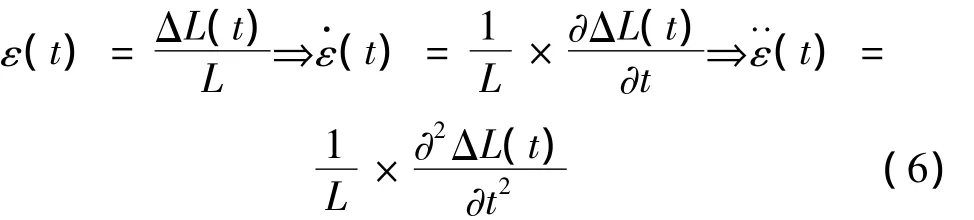
利用式(2)讨论惯性效应对试验结果的影响，在公式(2)中 ρ=2400kg/m3，A=17662.5mm2，L=450mm。唯一的未知因素是(t)。由式(6)可知，求(t)的关键因素在于ΔL(t)。利用试验结果把ΔL(t)拟合成t的三次方多项式，设，以应变率为 10－3/s工况下的试验数据为例进行拟合:A=－2.66×10－5;B1=2.32 ×10－4;B2= －2.73 ×10－4;B3=1.85 ×10－4。

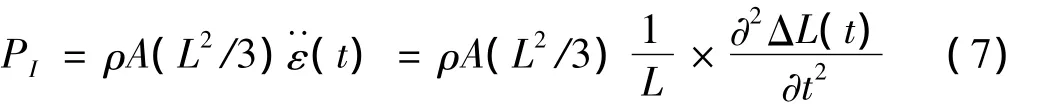
Max_PI=11.08 kN;Max_σPI=0.63 MPa;

同理可对其它几种应变率情况下的试验数据拟合分析，不同应变率下等效惯性力的极值汇总如表1所示:

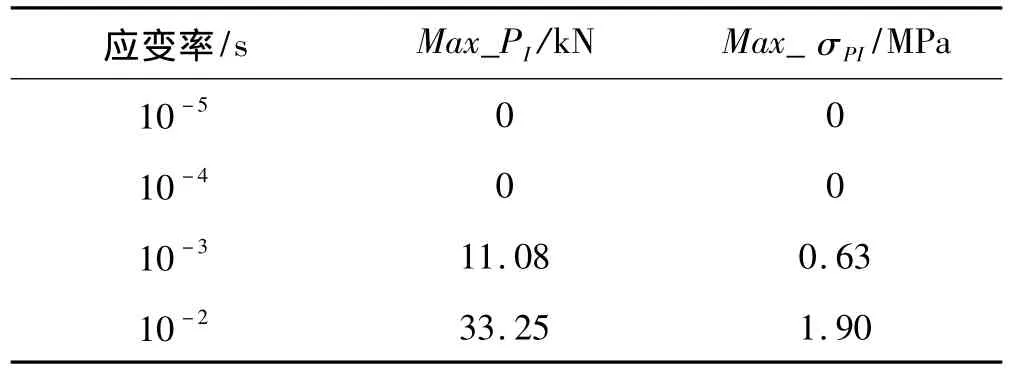
表1 不同应变率下PI的极值汇总Tab.1 Maximums at different strain rates

式(2)是基于将压力传感器置于加载端而推导得出的，由表1中的数据可知，在应变率为10－2/s时，惯性效应开始趋于明显，如果将压力传感器置于加载端，则因惯性效应会得到较大的压力值。Chung［13］在0.1/s～1/s应变率范围内对比研究了压力传感器分别置于加载端和固定端传感器测量值的大小，得出了将压力传感器置于固定端可以有效地降低惯性效应对测量值的影响。在本试验中，将压力传感器置于试件的固定端，压力传感器的测量值已经比较准确。综合试验结果和数据分析来看，在10－5/s～10－2/s范围内，可以忽略惯性效应对试验结果的影响。

2.2.3 应力、应变的不均匀性

在单轴抗压试验中，对于同一个试件上不同的引伸计的测量结果是不完全重合的，甚至相差的比较大，如图3所示;有三个因素可能导致了测量结果的差异性:① 试件两端不完全水平，单轴受压时，可能出现试件端面的局部先受压，进而导致某一侧的引伸计先有读数;② 试件长度为450mm，测量标距为300mm，试件在受压过程中，在长度方向的变形存在不均匀性;③测量误差。

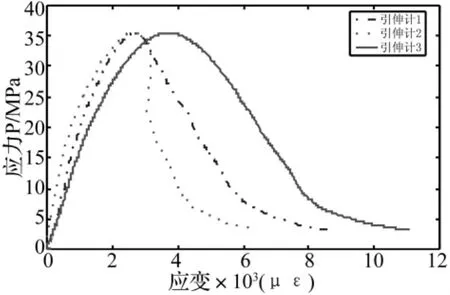
图3 不同引伸计测得的应力－应变曲线Fig.3 σ－ε curves from different extensometers

针对以上误差因素，在试验过程中可采用以下几点来尽量降低其对试验结果的影响。① 以准静态应变率对柱试件进行预压，并在预压过程中，观察加载板与试件端部接触是否紧密，如果有空隙可通过进一步的打磨端面来校正。② 安装引伸计时，尽量使引伸计距离试件两端的距离相等，并尽量保持竖直。③ 试验结束后，观察试件的破坏形态，看传感器是否还粘结在试件表面，对剥落的传感器，要注意其对试验结果的影响。

2.3 抗压强度

图4为混凝土抗压强度与应变率的关系图，从图中可以看出，随着应变率的增加混凝土抗压强度有明显的增加。以应变率10－5/s时的强度为准静态抗压强度，当应变率为 10－4/s、10－3/s、10－2/s时，混凝土的抗压强度分别平均增加了 7.45%、19.51%、29.23%。

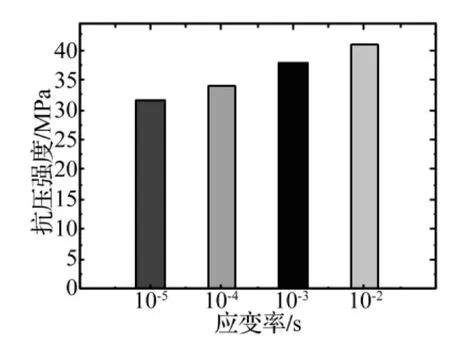
图4 混凝土抗压强度与应变率的关系Fig.4 Relationship of compressive strength and strain rate

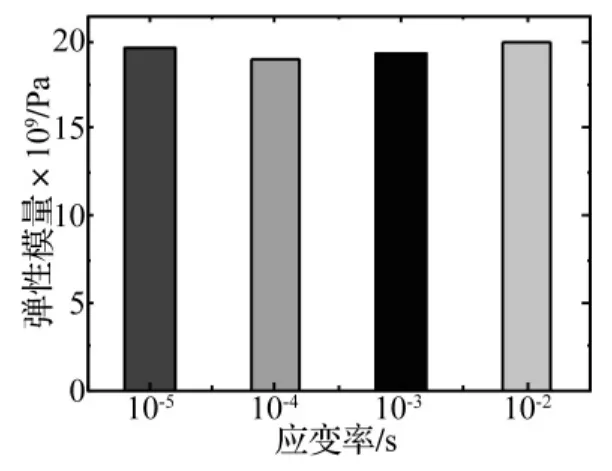
图5 弹性模量与应变率的关系Fig.5 Relationship of elastic modulus and strain rate

图6 峰值应变与应变率的关系Fig.6 Relationship of peak strain and strain rate

2.4 弹性模量

混凝土材料应力－应变关系曲线起始点的切线弹性模量在试验中测试的难度比较大，并且由于试验数据的离散性，难以精确测量。从图2中可以看出混凝土在受压初期处于弹性阶段，应力应变曲线基本上为一直线。本文将30%峰值应力处所对应的割线弹性模量作为混凝土的弹性模量。则不同应变率下的弹性模量计算结果见图5，从图中可以看出不同应变率下混凝土弹性模量的变化不大。对于线弹性材料例如钢材，它弹性模量的率敏感性就比较低。所以可以认为混凝土材料弹性模量的变化来自于试件微裂缝的开展。进而可以认为初始弹性模量不会受到应变率的影响，因为在加载的初始阶段，即在应力状态比较低的情况下，微裂缝的开展非常的不明显。

2.5 峰值应变

混凝土的峰值应变定义为受压时峰值应力处的应变。就目前的研究而言，对混凝土峰值应变与应变率的关系也存在争论。图6给出了峰值应变与应变率的关系。混凝土的峰值应变受应变率的影响是非常明显的。以应变率为10－5/s时的峰值应变为准静态峰值应变，当应变率为 10－4/s、10－3/s、10－2/s时，混凝土的峰值应变分别平均增加了 8.97%，25.84%，47.69%。

2.6 吸能能力

混凝土的吸能能力是研究混凝土产生裂缝以至发生破坏所吸收能量的物理量，反映了材料内在力学性能的大小。本文将混凝土的吸能能力定义为到达峰值应力时应力－应变曲线下面的包络面积。从图7中可以看出随着应变率的增加，混凝土的吸能能力也随之增加，而且增加的幅度非常明显。当应变率为10－2/s时，混凝土材料的吸能能力比准静态应变率下混凝土材料的吸能能力增长了约一倍。从损伤的角度来讲，材料的损伤破坏过程遵循着最小耗能原理，即破坏路径是沿着薄弱的环节和部位。在试件承受动力作用时，材料不能够自主的选择准静态工况下最薄弱部位作为破坏路径，只能选择与当前应变率相关的最小耗能过程进行破坏，这样就增加了材料的弹性变形能和塑性耗能。随着应变率的增大，材料的自主选择能力减小，材料表现出更大的吸能能力。

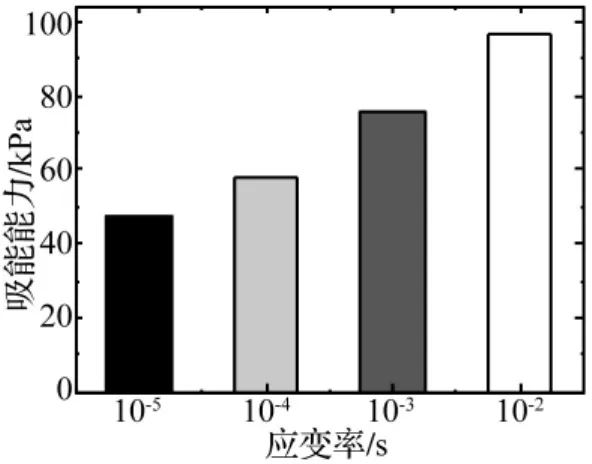
图7 应变率与吸能能力的关系Fig.7 Relationship of energy absorption capacity and stain rate

2.7 破坏机理分析

图8给出了柱试件在不同应变率下的破坏形态。混凝土是脆性材料，其由三相介质组成，粗骨料、水泥基质、以及骨料与水泥基质之间的交界层组成。养护完成后的混凝土柱在未受荷载前其内部已经存在大量的微裂缝，这一部分是自由水蒸发以后留下的微孔隙，还有一部分是温度应力等原因引起的微裂缝。这些微裂纹在承受载荷时，必定有一条或数条较大的裂纹优先扩展形成主裂纹。在准静态条件下，主裂纹有足够的时间形成和扩展，最终形成贯穿裂纹，在高应变率加载条件下，主裂纹来不及扩展，冲击能量被试件中的微裂纹和弱界面吸收，形成多点微裂纹同时起裂。这些微裂纹使试件破坏时碎块较小，表现出不同于静态加载下的破坏模式。混凝土强度的增加主要是由于随着应变率的增加，混凝土在破坏时砂浆基体内部微裂缝来不及充分扩展，因而导致了混凝土骨料的破坏，应变率越高，混凝土骨料破坏得越多，从而混凝土的强度就越高。试验现象也能明确地解释这个结论:从破坏断裂面上来看，发现随着应变率的增加，断裂面上破坏的骨料明显增多。

图8 试件破坏形态Fig.8 Fracture pattern

3 结论

本文通过混凝土柱的轴心动态抗压试验，在10－5/s～10－2/s应变率范围内，系统研究了应变率效应对混凝土抗压强度、弹性模量、峰值应变、吸能能力以及破坏机理的影响，定量评价了试验机刚度和惯性效应对试验结果的影响。

(1)在不同应变率的动荷载作用下，混凝土的应力－应变全曲线与静荷载下测得的全曲线在形状上基本一致。以应变率10－5/s时的强度为准静态抗压强度，当应变率为 10－4/s、10－3/s、10－2/s时，混凝土的抗压强度分别平均增加了 7.45%、19.51%、29.23%。

(2)不同应变率下混凝土的弹性模量变化不大，峰值应变具有一定的离散性，但总体的趋势是增加的。

(3)随着应变率的增加，混凝土柱试件表现出更大的吸能能力，试件断裂面上破坏的骨料明显增多。

(4)混凝土试件采用不同的试验方法测定应力－应变全曲线时，试件应变率的变化规律是不同的，刚性元件的使用使试件应变率的变化幅度变小，增加了试件应变率的稳定性。

(5)惯性效应在10－2/s应变率时，开始趋于明显，但将压力传感器置于固定端，可以忽略惯性效应对压力传感器测量值的影响。

［1］Javier Malvar L，Allen Ross C.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1998，6:735－739.

［2］林 皋，陈健云.混凝土大坝的抗震安全评价［J］.水利学报，2001，(2):8－15.

［3］Comite euro-international du beton.CEB-FIP MODEL CODE［S］，1990.Wiltshire Redwood Books，1993.

［4］Curione C.Influence of dynamic loading on structural design［J］，Ziviler Luftschutz，1958，22(2/3):58 －66.

［5］ASCE.Design of structures to resist nuclear weapons effects［M］，Manual No.42.

［6］Bischoff P H.Compressive behaviour of concrete at high strain rates［J］. Materials and Structures，1991，24:425－450.

［7］闫东明，林 皋，徐 平，等.混凝土双轴动态试验及其数据处理方法［J］.哈尔滨工业大学学报，2009，41(6):160－163.

［8］Yan D M，Lin G.Influence of initial static stress on the dynamic properties of concrete［J］.Cement ＆ Concrete Composites，2008，30:327 －333.

［9］闫东明，林 皋，刘钧玉，等.不同环境下混凝土动态抗压特性试验研究［J］.大连理工大学学报，2006，46(5):707－711.

［10］闫东明，林 皋，刘钧玉，等.定侧压下混凝土的双轴动态抗压强度及破坏模式［J］.水利学报，2006，37(2):200－204.

［11］肖诗云，田子坤.混凝土单轴动态受拉损伤试验研究［J］.土木工程学报，2008，41(7):14－20.

［12］肖诗云，田子坤.历经荷载历史混凝土动态受拉损伤试验研究［J］.工程力学，2010，27(1):123－128.

［13］Chung H W.Shear strength of concrete joints under dynamic loads［J］.Concrete，1978，12(3):27－29.