基于有限元的异步电机电磁振动分析

王 玎，祝长生，符嘉靖

(浙江大学 电气工程学院，杭州 310027)

电机的振动分别由电磁振动、机械振动、气体振动三部分组成［1－4］。电磁振动是由电机气隙中磁场的相互作用，在转子和定子上产生随时间和空间变化的电磁力，使电机产生振动。机械振动是由转子的不平衡、轴承等机械结构或装置引起的振动。气体振动是由电机通风部件中的空气流动或由空气动力引起的振动。对于现代的大中型电机，由于多采用高阻尼低噪声的滑动轴承及对旋转部件作严格的动平衡，电机的机械振动并不严重。在转速不高的电机中，气体振动一般也不突出。因此，电磁振动就成为许多大中型电机的主要振动源。由于电机的电磁振动是电机电磁场和电机结构相互作用的结果，那么利用磁－固耦合振动理论来研究电机的电磁振动是寻找电机电磁振动产生机理以及解决电机电磁振动最有效的方法［5－6］。

利用磁－固耦合振动理论来研究电机的电磁振动需要解决电磁力的准确计算和电机结构振动响应分析两个问题。电机电磁力的计算一般采用近似解析法和数值分析法。近似解析法利用气隙磁导和磁势来计算气隙磁场产生的电磁力。这种分析方法起源于上世纪40年代，首先是针对感应电机、同步电机和直流电机［1－6］，目前也被用在开关磁阻、永磁等电机电磁力的分析上［7－11］。数值分析法是随计算电磁学和计算机的发展迅速发展起来的一种数值方法。这种方法能够考虑的因素较多，特别是各种商用电磁场分析软件的普及和应用，目前已经是电机电磁特性分析中十分普遍的方法。由于电磁力是电机电磁振动的激励源，其计算的精度决定了电机电磁振动的计算精度，所以目前在电机电磁振动的研究中大多采用数值分析法来计算电机的电磁力。胡敏强等［12］对异步电动机的运动有限元、场路耦合时步有限元法等进行了介绍。Sakamoto等［13］先用有限元法计算异步电机的电磁力，然后分析电磁力的高次谐波引起的定子振动。张凤阁等［14］先用有限元法分析感应电机的电磁场，计算得到电磁力后，再计算在其作用下电机的谐响应。Christoph等［15］利用有限元法计算感应电机定子上的电磁力，再计算电机定子的振动特性。

本文利用有限元法，将电机的电磁场分析和结构振动分析相结合，研究电机的电磁振动。首先利用ANSOFT有限元法软件对异步电机内的电磁场进行瞬态分析，得到电机内的电磁场，进而得到稳定转速下电机定子上受到的时变电磁力。其次用ANSYS有限元软件建立电机定子结构的三维模型，以瞬态电磁场得到的时变电磁力为基础，并利用频谱校正技术准确地确定各谐波激励的幅值，然后进行电机定子结构的响应分析，得到在电磁力激励下电机定子结构的振动响应。通过分析电机定子结构的振动特性，以指导电机电磁参数选择和结构的优化，达到降低电机电磁振动的目的。

1 电机的电磁场分析

为了计算电机定子上的电磁力，首先按照异步电机的几何尺寸和电磁参数，在ANSOFT软件中建立其电磁场有限元法分析模型，然后用时域瞬态分析方法计算出电机从启动到给定转速稳定过程中的电磁场以及定子齿上的电磁力。

对于一个轴向较长的电机，端部效应的影响可以忽略。如果再进一步假设磁路所在平面与电机轴向是正交的，那么可以用二维的模型进行分析。若不满足这些简化条件，则需要采用三维模型。

对表1的55 kW的三相异步电机，建立的电机电磁场模型如图1所示，其中包括定子冲片、转子冲片、转子铝条、定子绕组以及空气隙。电机材料采用实际的B－H曲线来考虑磁饱和的影响。

表1 55 kW异步电机基本参数Tab.1 Basic parameters of an asynchronous motor

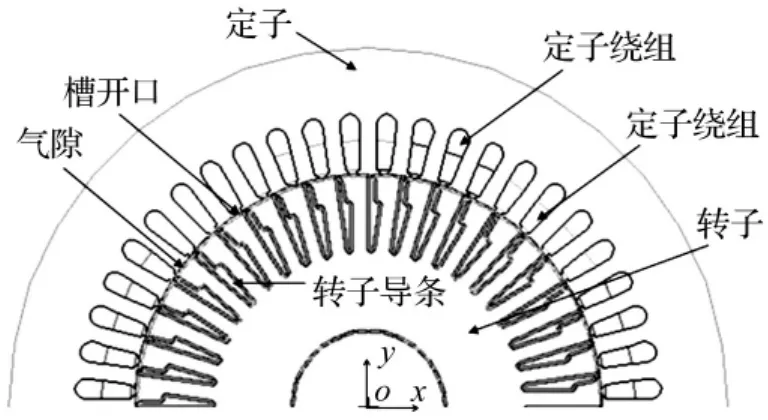
图1 电机的二维电磁场模型Fig.1 2-dimensional electromagnetic model of the asynchronous machine

由于电机的电磁力中含有多个高频谐波分量，因此在进行电磁场有限元时域瞬态分析时，电机电磁场分析的步长要足够小，这样才能获得电机主要谐波频率的电磁力。

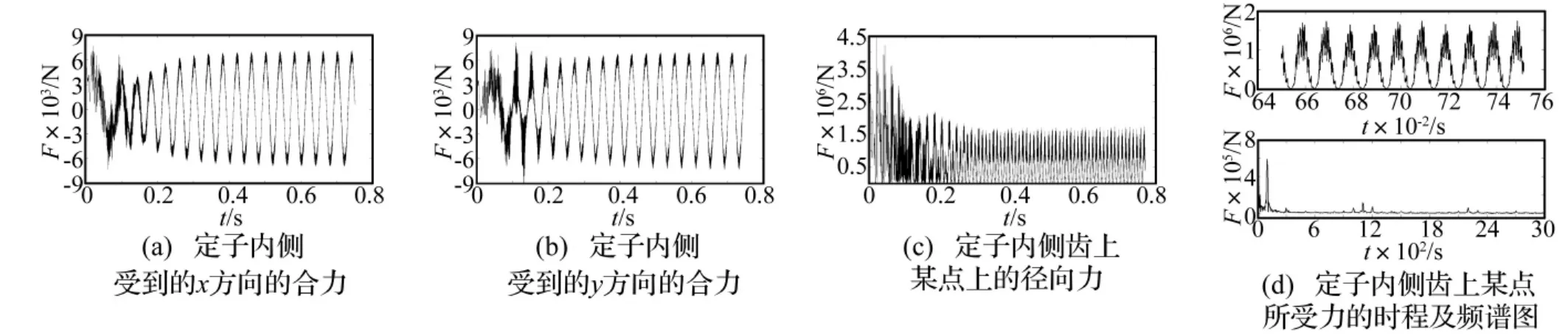
图2 ANSOFT计算得到的激励力Fig.2 The electromagnetically excited force calculated by ANSOFT

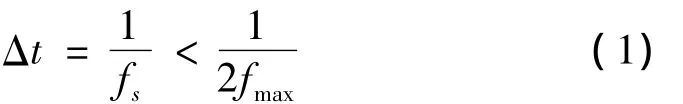
在以Δt为时域瞬态求解步长的情况下，利用FFT获取信号频率的分辨率Δf为:

其中N为FFT计算的长度［16］。

定子齿上受到的电磁力用麦克斯韦张力法计算。假设受力物体表面S上的磁场强度为H，并且这个物体外部被空气所包围，则这个物体受到的电磁力为［17］:

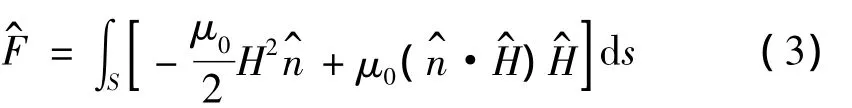
将力分解在x和y方向，则:

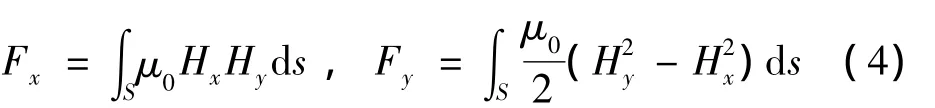
其中μ0为空气中的磁导率，为沿表面S法线方向上的单位矢量，Hx和Hy分别为受力物体表面S上x和y方向上的磁场强度。

图2分别给出了电机从静止运行到额定转速的过程中，用ANSOFT计算得到的定子内侧x和y方向的力Fx和Fy、定子内侧齿上某点上受到的径向电磁力F1的时程曲线以及电机进入稳态后定子内侧齿上某点电磁合力的时程曲线及频谱图。由图2(c)可以看出0.5 s后电机逐渐进入稳态，因此在图2(d)中选取0.6 s后的稳态数据来进行FFT分析。

图3和图4分别为某一时刻电机内磁力线和磁密分布。可以清楚地看到电机四个极的位置，磁密在定、转子齿的顶部最大。

从1999—2008年，国土资源部在地质灾害易发的1 640个丘陵山区县部署完成了1∶20万比例尺地质灾害调查，查出24万处隐患点。这只是初步摸底，此项工作还应进一步推进。灾害风险评估是将灾害防治工作前移，从根本上预防风险，是现代风险管理的本质，需要政府主管部门具有前瞻性、超前意识和长远意识。

电磁力的主要谐波数是由电机的齿槽等参数决定的，理论上力波的主要频率成分与从图2(d)中得到的电磁力主要频率如表2所示。可以看出理论得到的主要谐波频率成分与从电磁力频谱分析得到的结果是一致的。FFT计算结果与理论计算结果之间有误差的原因在于数字FFT的分辨率所致。

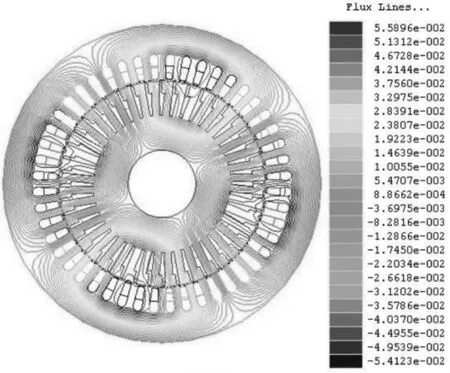
图3 某时刻电机内磁力线分布图Fig.3 Flux lines distribution in asynchronous machine

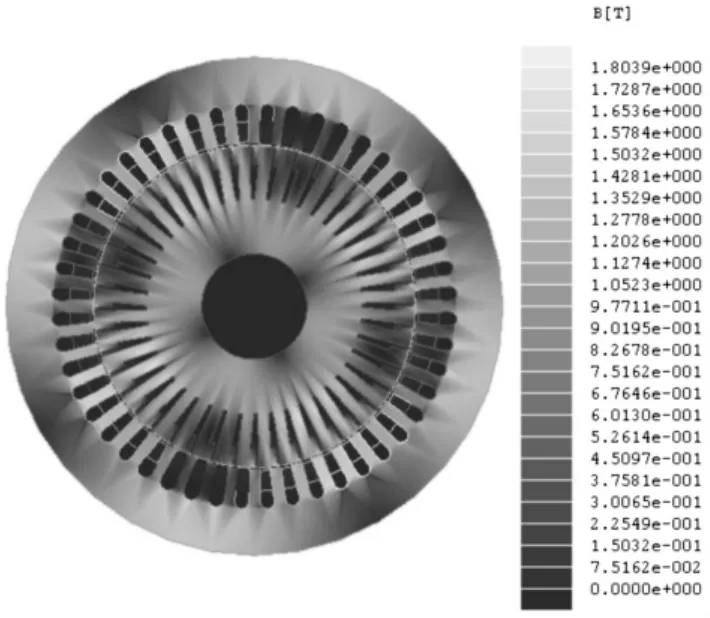
图4 某时刻电机内磁密分布图Fig.4 Flux－ density distribution in the asynchronous machine

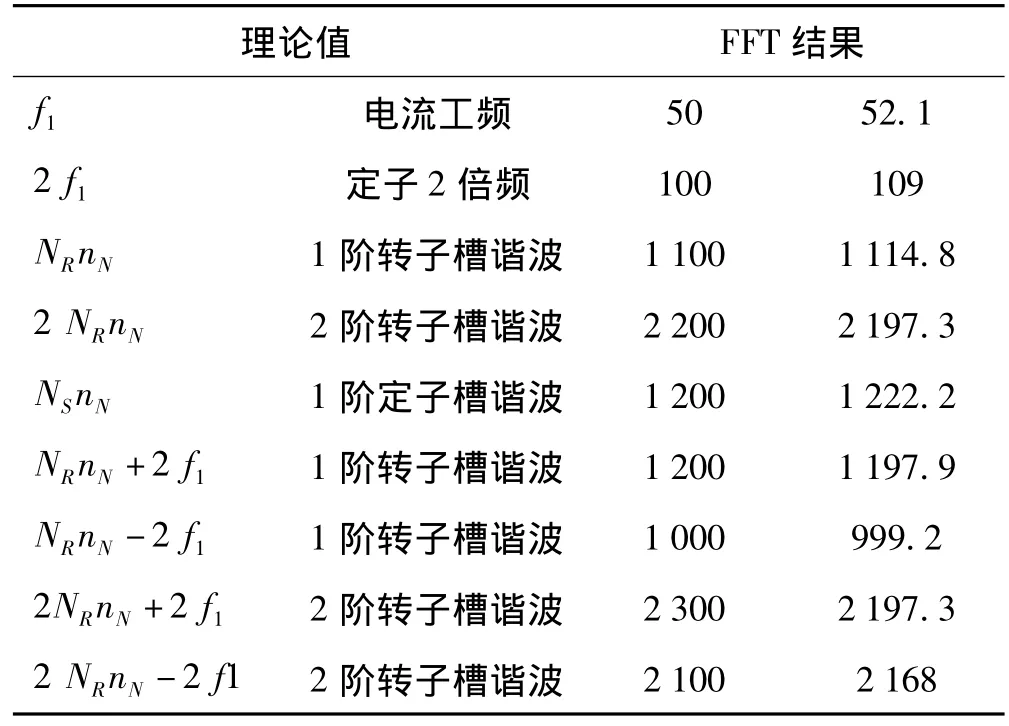
表2 电机主要谐波频率成分(Hz)Tab.2 Significant harmonic frequencies(Hz)

图5为定子内侧x方向稳态电磁力的时间历程曲线和频谱特性。结果说明了，电机定子在x方向的主要谐波频率范围为0Hz～3000Hz。电机定子内侧y方向上稳态电磁力的主要谐波频率范围也在这个频率范围内。

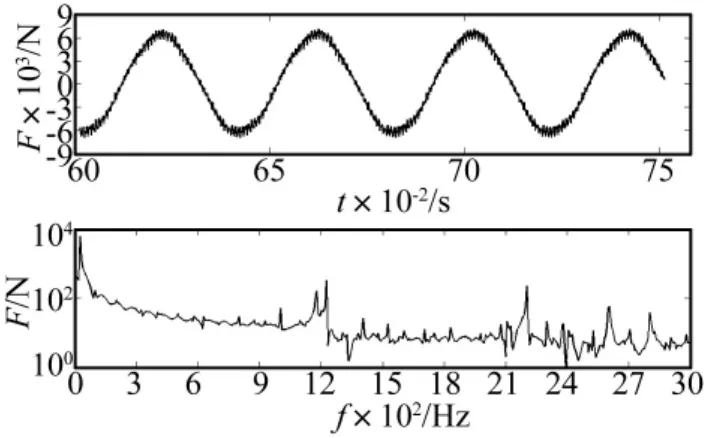
图5 定子内侧x方向的电磁力时间历程和频谱特性Fig.5 Time history and spectrum distribution of the given surface-force in x-direction of the stator

2 电机结构的振动特性分析

电机的振动特性是指电机结构在受到一定载荷作用下的响应。利用ANSYS有限元软件建立该电机三维结构的有限元模型，再以时域瞬态电磁场分析得到的稳态电磁力作为激励，进行电机结构的响应分析，得到在电磁力激励下电机的振动特性。

利用有限元法容易建立电机结构振动的运动微分方程为:

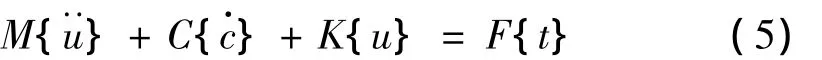
其中{u}为广义坐标，M、C和K分别为电机结构的质量、阻尼和刚度矩阵，F(t)为激励力。

在ANSYS中建立的该电机定子结构的有限元模型如图6所示。

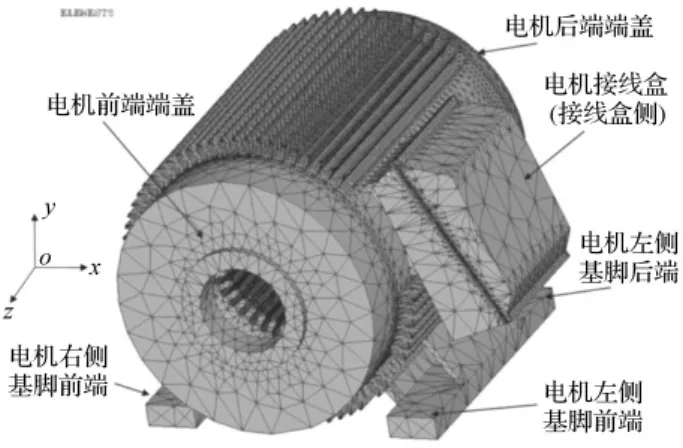
图6 电机结构分析的有限元模型Fig.6 FE model of the asynchronous machine

电机在实际工作时，基脚固定在基础上，因此电机的振动分析是在定子基脚零位移约束状态、电机定子内表面受到一个旋转激励力的条件下计算得到的。为了计算方便，定子铁芯内表面上旋转的单频激励力分别用垂直和水平方向上的周期激励力来模拟，施加的激励力为其稳态部分。

在恒幅激励力的作用下，计算得到在0Hz～3000Hz的频率范围内，电机定子结构上最大振动位移随激励频率的变化如图7所示。

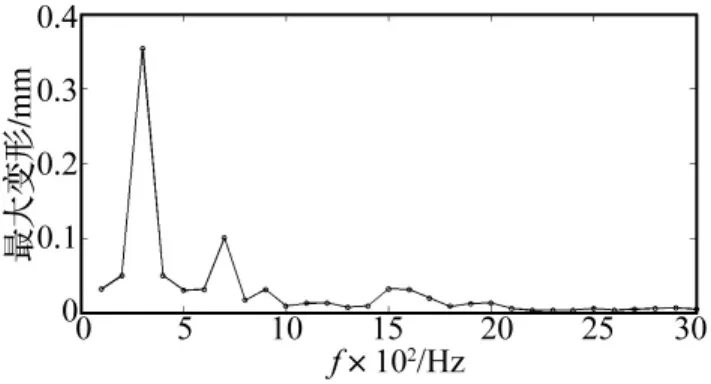
图7 电机结构上的最大振动随激励频率的变化Fig.7 The maximum deformation of asynchronous machine

随着激励力频率的增加，电机定子结构上最大振动呈下降趋势。因此在研究电机的电磁振动时，应着重考虑低频范围内电磁力的作用。实际上电机在低频和高频范围内的振动形式是不同的。在低频范围内，电机定子主要呈现出整体的变形，如图8电机定子整体发生偏移;在高频范围内，电机定子整体变形较小，局部变形较大，如图9电机定子变形很小，但在接线盒和后端盖上则出现了较大的变形。

图8 激励为100Hz时电机的谐响应Fig.8 Harmonic response excited by 100Hz

图9 激励为2200Hz时电机的谐响应Fig.9 Harmonic response excited by 2200Hz

在电机上的不同位置，振动响应的大小以及变化规律是不同的。实践中常以电机基脚作为考察点。表3比较了电机前端盖上左侧(无接线盒侧)、右侧(接线盒侧)、顶部和左侧基脚位置的谐响应。对于电机前端盖顶部以及左右两侧这三点来说，水平方向(x)的振动最大，垂直方向(y)其次，轴向(z)的最小。在x方向上，位移最大的是在端盖顶部。在y方向上，位移最大的是位于端盖左侧的节点，右侧的位移较小，端盖顶部和底部的位移更小。在z方向上，端盖顶部的位移最大。由于端盖底部靠近基脚，受到基脚位移约束的影响，端盖底部在各个方向上的位移都很小。

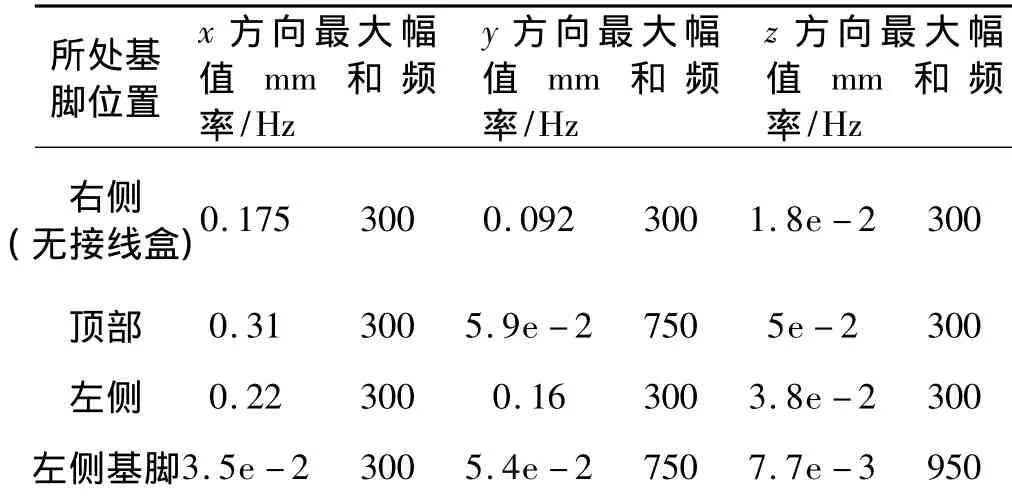
表3 电机前端盖上的谐响应Tab.3 Harmonic response on the front cover of the machine

表4比较了电机接线盒顶部、低部的谐响应。可见电机接线盒上部x、y和z方向上的振动依次减小;电机接线盒底部，y方向位移最大，x方向次之，z方向最小。电机接线盒顶部底部的x和y方向上最大振动均大于端盖上各位置相应的最大振动，振动非常剧烈。

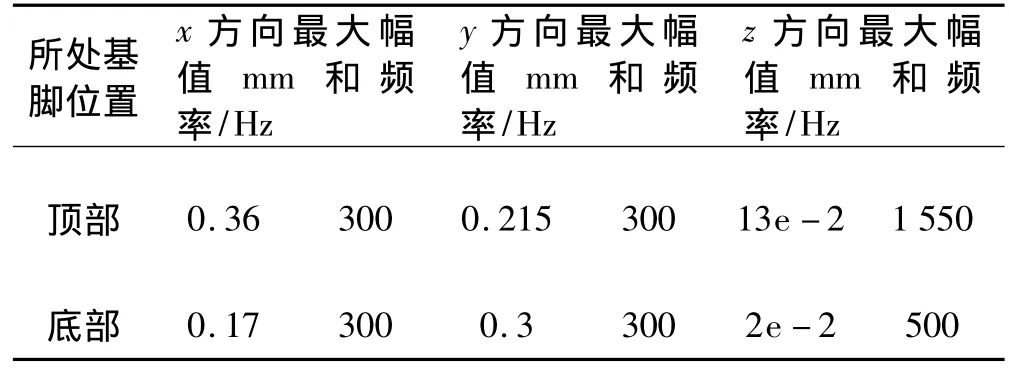
表4 电机接线盒上的谐响应Tab.4 Harmonic response on the junction box of the machine

表5比较了电机左右端基脚前后位置的谐响应。结果表明，与电机上选取的其它部位相比，特别是在x方向上，基脚上最大振幅小了很多。其主要原因在于计算中对基脚做了零位移约束，所以基脚上各个方向上的振动都很小，各方向之间也没有明显差异。

无论是电机端盖、接线盒还是基脚，其最大振幅出现的频率值大都集中在300Hz和700Hz附近，即电机定子低阶模态频率值附近。可见低阶模态对电机结构的振动特性影响很大。

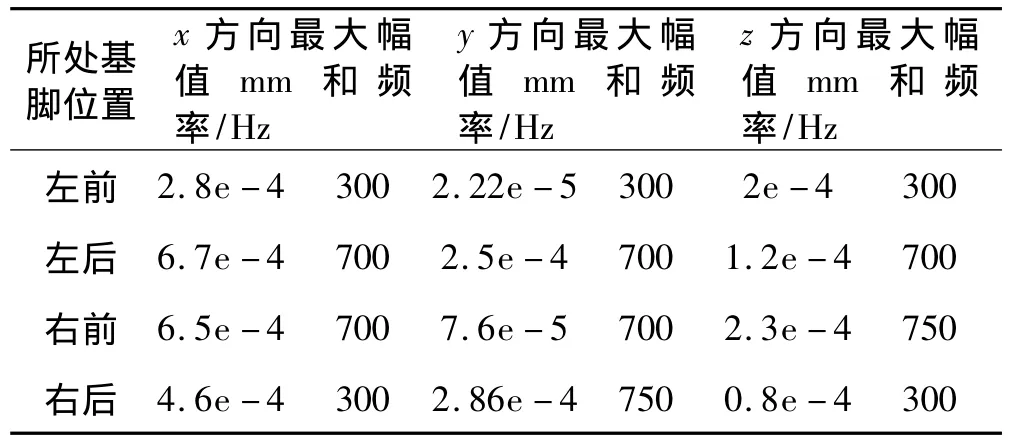
表5 电机左、右基脚上前后端上的谐响应Tab.5 Harmonic response on the feet of the machine

对于电机来讲，电机的电磁力是随频率变化的，为了得到电磁力在各个频率上的幅值，需要对时域瞬态电磁场得到的时变电磁力的时程数据进行频谱分析。频谱分析一般是利用离散FFT进行的，但是FFT后得到的频谱，无论是频率、幅值还是相位，都可能存在一定的误差。这主要是由两方面的原因引起的:其一是由于没有对时域信号进行整周期截断，导致对其进行离散FFT时得到的频率、幅值和相位产生误差;其二是由于多频谐波信号之间的干涉现象产生的误差。为此利用离散频谱校正技术［16］对力波的幅值逐一进行了校正，表6为经过频谱校正后得到的主要频率电磁力的幅值。

基于表6中电磁力波，计算电机定子的谐响应，特别是基脚上的加速度。由于电磁力的谐波较多，而电机定子结构模态的频率又十分密集，因此在电磁力的每个谐波附近，都可能存在着与电机定子结构的固有频率十分接近的情况。但是由于电磁力波与电机定子模态的阶次不同，电磁力的影响也不同。只有在电磁力的力波与电机定子模态的阶次相同的条件下，电机定子才会出现明显的振动。图10比较了在表6电磁力作用下电机定子右侧基脚前端、右侧基脚后端、左侧基脚前端和左侧基脚后端各方向上最大加速度的变化情况。

电机基脚加速度有3个主要的峰值频率，分别是25Hz、100Hz和1200Hz。而这三个频率下的激励力幅值也是最大的。电机的振动频率与激励力的频率是一致的。特别是在25Hz的情况下，由于电磁激励力的幅值很大，所以在该频率下电机的振动十分明显。当激励力的频率大于2000Hz后，尽管力的幅值可能会大于某些低频激励力(如150Hz和1000Hz)，但电机基脚上的加速度并不大，有些甚至更小。因此低频激励力对电机振动特性的影响比较大，高频的激励力影响较小。

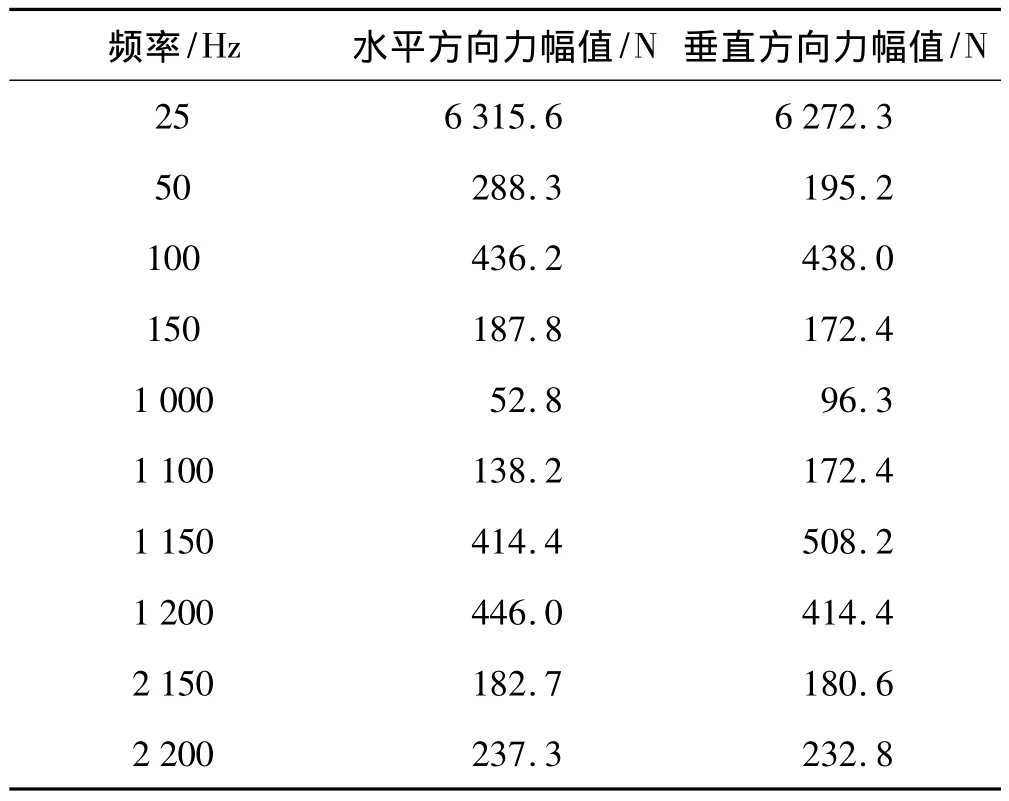
表6 频谱校正后电机定子上电磁力的幅值Tab.6 Exciting forces after spectrum correction

图10 电机左右基脚前后位置各方向上的加速度Fig.10 The accelerations in x，y，z direction on the front and back sides of each foot

3 结论

本文首先对异步电机的电磁场进行分析，得到了电机从启动到稳态过程中的电磁力。将电机稳态下定子受径向电磁力进行傅立叶分析和校正计算，得到电磁力的谐波成分。在ANSYS中建立了电机结构的三维模型，进行电机在不同电磁力激励下的谐响应分析，确定电机的电磁振动。得到的主要结论如下:

电机电磁力的谐波频率主要是由电机定转子齿槽数决定的。

电机定子固有频率分布密集，在电磁力的谐波频率附近都存在着多个固有频率，对电机振动特性的影响低频率的激振力较大，高频率的激振力对电机振动影响较小。

采用离散频谱校正技术可以较准确地确定各谐波电磁力的大小。

［1］舒波夫.电动机的噪声和振动［M］.沈官秋译.北京:机械工业出版社，1980.

［2］Yang S J.Low －noise electrical motors［M］.Clarelldon Press，1981.

［3］Timar P L.Noise and vibration of electrical machines［M］.Elsevier Science Pub，1989.

［4］陈永校，诸自强，应善成.电机噪声的分析和控制［M］.杭州:浙江大学出版社，1987.

［5］邱家骏.机电耦联动力系统的非线性振动［M］.北京:科学出版社，1996.

［6］Jacek F G，Chong W，Joseph C L.Noise of polyphase electric motors［M］.CRC Press，2006.

［7］孙剑波.开关磁阻电机的减振降噪和低转矩脉动研究［D］.武汉:华中科技大学，2005.

［8］于镇波.永磁同步电机振动与噪声特性研究［M］.沈阳:沈阳工业大学出版社，2006.

［9］Husain I，Radun A，Nairus J.Unbalanced force calculation in switched－ reluctance machines［J］.IEEE Transactions on Magnetics，2000，36(1):330 －338.

［10］Zhu Z Q，Howe D，Bolte E，et al.Instantaneous magnetic field distribution in brushless permanent magnet DC motors，part I:open－circuit field，part II:armature－reaction field，part III:effect of stator slotting，part IV:magnetic field on load［J］.IEEE Transactions on Magnetics，1993，29(1):124－158.

［11］Huang S R，Aydin M，Lipo T A.Electromagnetic vibration and noise assessment for surface mounted PM machines［M］.Proceedings of Power Engineering Society Summer Meeting，2001，(15－19):1417－1426.

［12］胡敏强，黄学良.电机运行性能数值计算方法及其应用［M］.南京:东南大学出版社，2003.

［13］Sakamoto S，Hirata T.Vibration analysis considering higher harmonics ofelectromagneticforcesforrotating electric machines［J］.IEEE Transactions on Magnetics，1999，35(3):1662－1665.

［14］Zhang F G，Tong N Z，Wang F X.Analysis of vibration modes for large induction motor［M］.Proceedings of Electrical Machines and Systems，2005，1:64 －67.

［15］Christoph S，Benedikt S，Michael V，et al.Electromagnetically excited andible noise-evaluation and optimization of electrical machines by numerical simulation［J］.COMPEL:The International Journal for Computation and Mathematics in Electrical andElectronicEngineering， 2007，26(3):727－742.

［16］丁 康，谢 明，杨志坚.离散频谱分析校正理论与技术［M］.北京:科学出版社，2008.

［17］颜威利，杨庆新，汪友华，等.电气工程电磁场数值计算［M］.北京:机械工业出版社，2005.