过程性：数学活动经验积累的应然之道

宋煜阳

如何有效积累数学基本活动经验呢？笔者以为，不论是经验的生成还是积累的进化，都需要以“过程性”为保障。这里所说的“过程性”，有两层含义：一是周期性，数学活动经验积累需要一定的时间为周期，并非一两节课或一两次活动就可以积聚；二是阶段性，数学活动经验也应像知识体系学习般螺旋上升，需要构建活动经验序列加以统领。笔者结合“等积变形”问题的分析，就如何从过程性的视角来积累数学活动经验谈谈自己的粗浅认识。

一、问题现象

在“长方体和正方体”单元学习中，很多学生会被“在一个长50厘米、宽40厘米、高30厘米的长方体玻璃缸中，水深20厘米，如果把一块棱长为10厘米的正方体铁块浸没于玻璃缸中，现在玻璃缸内水深多少厘米？”之类等积变形的问题所纠结。

多数学生第一次面对这类问题，存有很大困难。这时，教师通常组织分析讲解，主要采用两种方式：一种是回忆描述讲解，组织学生回忆“乌鸦喝水”故事（该素材在人教版教材中是作为“体积”概念教学引入），然后组织学生讨论“正方体铁块放下去，水面为什么会升高？”揭示“水面升高部分的体积就是正方体铁块的体积”；另一种是直观演示讲解，提供玻璃缸实物结合题意进行直观演示，讨论讲解揭示“水面升高部分的体积就是正方体铁块的体积”。实际教学显示，第二种讲解方式效果略好于第一种，但仍有不少学生无法真正理解“等积变形”。

二、分析改进

这表明，等积变形的问题不是靠教师“讲”清楚就能解决，更有赖于学生内化的经验“悟”明白。在上述两种讲解方式中，第二种直观演示讲解能够帮助学生获得经验，不过此时获得的是一种替代性经验，不是直接经验。在实际教学中，由于教学时间所限，设计具有意义的活动让学生获得替代性经验是非常必要的，也是积累数学活动经验常见的方法。值得我们思考的是，为什么教师直观演示、思考讨论、讲解点拨都具备了，学生还不能真正理解、有效建立起经验呢？这需要沿着“学习困难—学习经验—学习活动”的路径进行分析，即需要分析“学生学习的真正困难是什么，是什么经验的缺失产生了学习困难，要积累此项经验需要开展怎样的活动，活动的内容、时机、频次、方式有什么要求”等一系列问题。

回到“等积变形”具体问题，笔者在访谈中发现，学生主要疑点集中于两个问题：①10×10×10=1000（立方厘米）是正方体的体积，怎么可以用它去除以50×40这个长方体的底面积呢？②铁块是固态的，怎么变成了液态的水呢？

学生产生这两个疑惑很正常。因为在先前体积学习中，只有长方体体积除以长方体的底面积才是高（水深），现在怎么可以用另一个物体（正方体铁块）的体积来除以长方体的底面积呢？这就产生了第一个疑点。第二个疑点，指向了较为复杂的替换，涉及了“正方体体积替换为等体积的长方体（水升高所形成的长方体部分）”“物体的固态（铁块）向液态（水）进行替换”两个跨度的替换；而要理解这些替换，需要从固态、液态同一性质材料相互替换（如长方体铁块锻造为正方体，长方体容器内的水倒入正方体容器）为基础，积累“体积不变，形状（表面积）变了”的活动经验。

问题在于，在这个替换的经验积累进程中，教师又安排了哪些跟进的活动呢？据笔者了解，在本单元教学中，多数教师只在“体积”概念教学中安排了一次演示活动（实物演示或课件演示），有的甚至连课件演示也没有安排。在“体积”概念中，学生对“空间”一词是很难理解的，实际教学确实如此。在“乌鸦喝水”演示活动中，学生能够体会到（也有一些学生积累了相关生活经验）“水”被“石子”压挤上来的空间，但仅凭此时的直观演示学生是无法建立起“压挤上来的空间等同于石子的体积”的经验。另外，从“所挤占的空间”的外延来看，可以是用石子挤占，也可以是等体积的其他形态材料（如液态的水，固态的沙子）进行挤占，只有当学生悟到“不管什么材料、什么形态，只要是等体积，就可以挤占同样大小的空间”，才有助于等积变形的本质理解。从这个角度分析，一两次的直观演示活动，是无法支撑起相应的经验建构的。

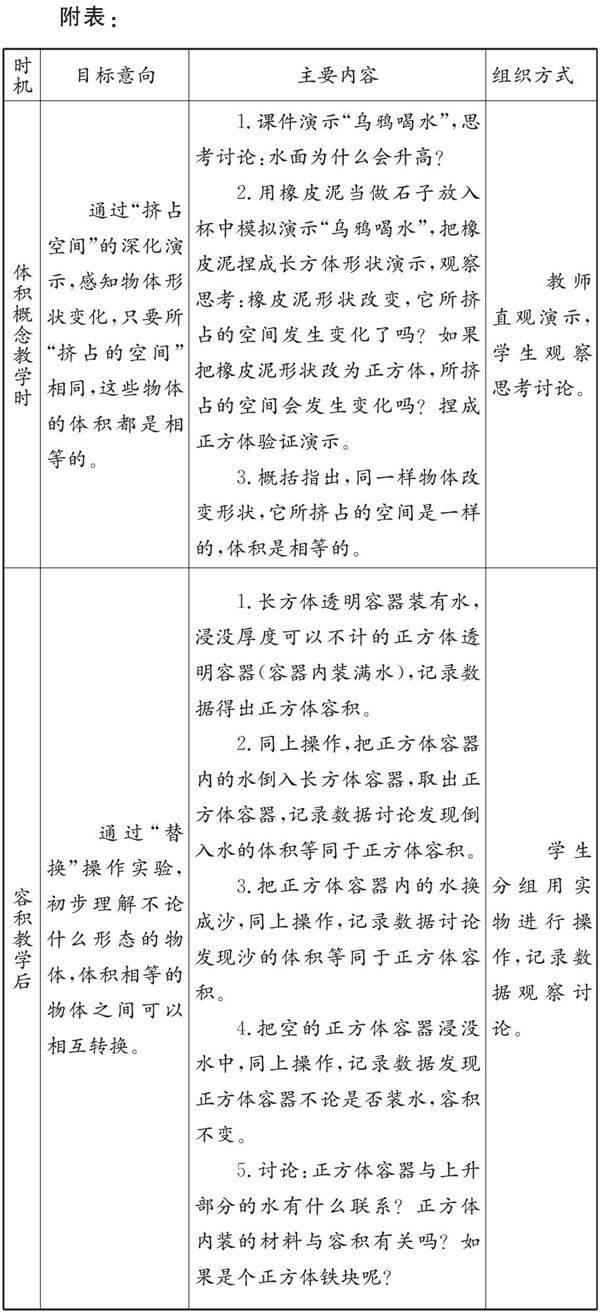
实践表明，关于等积变形问题要关注以下两个时机的活动开展（见附表）。

三、衍生思考

在数学活动经验积累中，教师们更为关注数学活动的设计与开展。但就过程性经验积累而言，笔者更愿强调一种整体架构的视野。如果不能从单元、学段统领的视角来规划、建立数学活动经验序列，数学活动就有可能是零星的、断层的，就会产生因基本活动经验积淀不到位而造成学习困难。

例如，“最少用（）个小正方体可以拼搭成一个较大的正方体”是学生在一年级下册“立体图形拼组”单元学习中遭遇的，到了五年级长正方体体积学习后再次面对同样的问题，仍然有部分学生犯一年级时的低级错误。这个现象至少表明一部分学生的经验并没有随着年级的升高而得到积累。为什么没有得到积累呢？就是因为在长达四年跨度的学习期间，除了一年级下册开展过操作拼搭活动外就不曾碰过类似的活动，整体架构的意识缺乏整整耽误了学生四年的积累时间。

因此，在数学活动设计中，教师要练就一双慧眼，善于根据知识体系结构瞻前顾后、追本溯源编制活动序列。例如正反比例概念教学中的数据观察经验可以追溯到中年级积、商的变化规律，甚至追溯到低年级的乘法口诀学习观察。

（作者单位：浙江省奉化市教师进修学校 责任编辑：王彬）