机织物顶破过程的有限元分析

张天阳，丁 辛，b

（东华大学a.纺织学院；b.纺织面料技术教育部重点实验室，上海 201620）

机织物顶破过程的有限元分析

张天阳a，丁 辛a，b

（东华大学a.纺织学院；b.纺织面料技术教育部重点实验室，上海 201620）

使用有限元分析软件ABAQUS模拟机织物的顶破过程，采用宏观、细观两种建模方法分析了顶破过程中机织物的应力应变分布、能量吸收机制以及摩擦作用的影响.研究结果表明，宏观建模方法能简单、快捷地预测机织物的顶破性能；细观建模方法可以详细地描述顶破过程中的纱线伸直、纱线滑移、纱线断裂和裂口延伸.模拟结果表明，织物主应变分布决定了顶破的破坏位置；主应力分布决定了破坏延伸方向.顶破发生前，纱线应变能是主要的能量转化方式；纱线发生断裂后，应变能部分转化为摩擦耗散能和纱线动能.另外，提高织物与顶破弹子之间的摩擦作用可以显著提升织物的顶破性能.

机织物；顶破；有限元分析；模型；能量转化；摩擦作用

顶破性能是机织物的一项基本力学性能.顶破测试使用球形弹子以恒定低速垂直作用于四周被固定的圆形织物平面［1］，依据弹子受力与位移曲线表征试样的顶破性能.但通过顶破测试很难得到顶破过程中的能量变化、应力分布等信息，难以得出织物的顶破机理.

有限元方法是分析织物顶破过程的有效工具，然而，迄今为止未见对织物顶破过程的有限元建模和分析，可以借鉴的研究集中在对织物弹道冲击过程的模拟上.TAYLOR等［2］从织物整体出发，建立了宏观有限元模型.在此基础上，TABIEI等［3］建立了反映织物拉伸、剪切等力学性能的宏观模型，但该过程需要大量的刚度矩阵推演和迭代，且更换织物所引起的模型变动较复杂.另外，由于宏观模型将织物视为各向同性的柔性薄壳，不考虑织物中交织着的纱线，虽可简化模型及计算，但难以反映织物中纱线应力、应变等细节.为了准确描述织物在载荷下的变形和失效，细观模型得以应用和快速的发展.文献［4-5］使用铰链连接的一维节点来模拟机织物交织，但该模型不能体现织物中纱线的相对滑移.文献［6-7］讨论了织物单胞的几何模型种类和分网方式，确立了一种能够较好反映织物拉伸、剪切性能的三维织物单胞模型.DUAN等［8］建立了三维平纹机织物的细观有限元模型，从纱线的角度反映织物弹道冲击性能，并研究了织物纱线之间的摩擦因数、边界条件以及弹头形状对织物弹道冲击的影响.RAO等［9］使用细观模型讨论了纱线力学性能对机织物弹道冲击的影响.

本文针对球形弹子低速顶破作用及机织物的组织结构特点，使用ABAQUS 6.9有限元分析软件，分别通过宏观和细观两种建模方法模拟织物的顶破过程，比较两种方法的特点.在此基础上，分析织物顶破过程中应力、应变分布情况和能量吸收方式，并讨论纱线间摩擦作用对顶破过程的影响.

1 机织物顶破宏观有限元模型

1.1 本构关系

本文的顶破试样为一块经重平组织的机织物，如图1所示.采用万能试验机对织物进行拉伸，拉伸速度为1.67 mm／s，经向、纬向和45°方向上的拉伸性能曲线如图2所示.由图2可以看出，除了每个方向上试样的拉伸性能为非线性外，各方向之间还表现出明显的面内各向异性.测试数据将应用于有限元模拟.

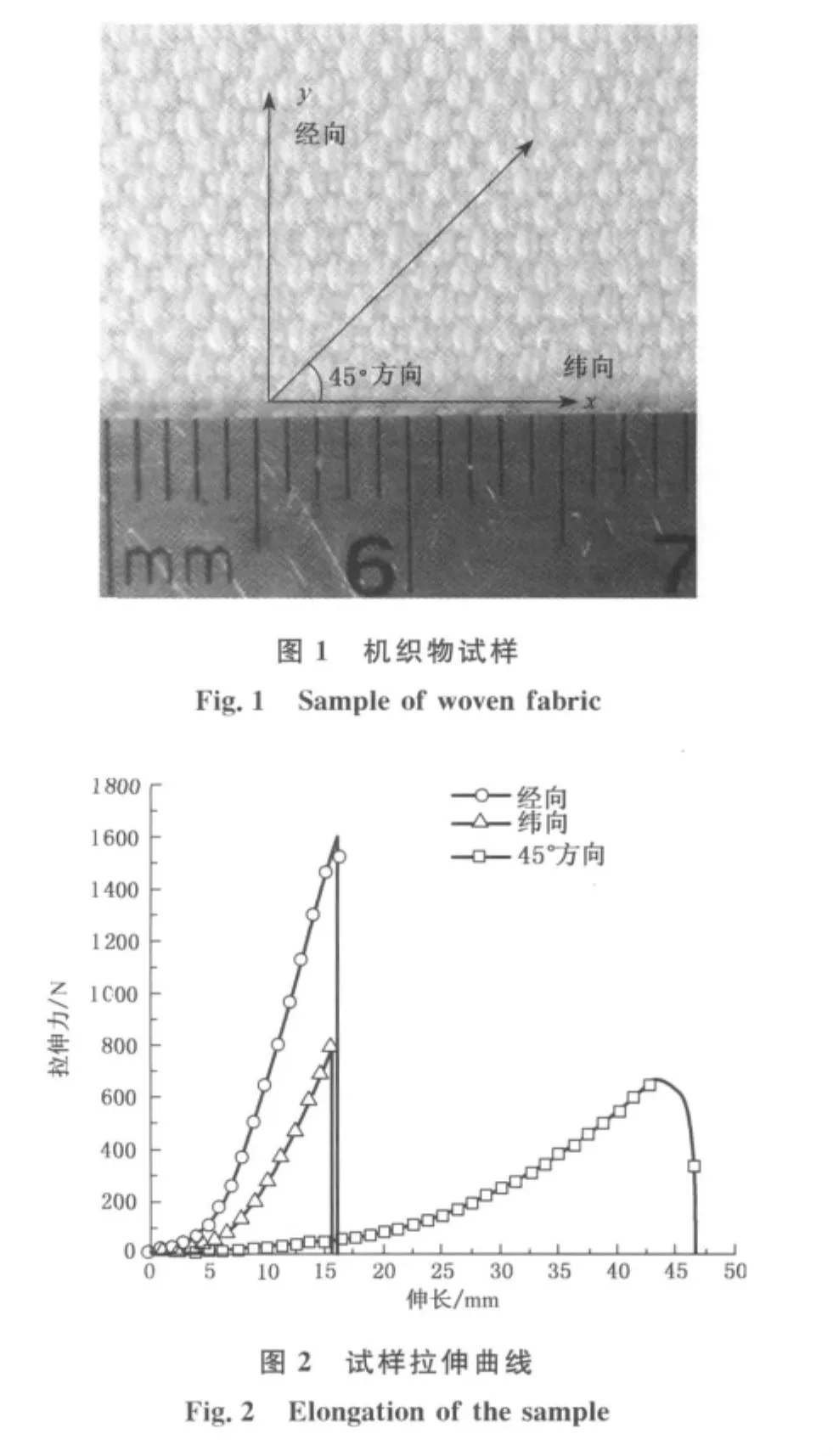
ABAQUS 6.9软件提供两种方法模拟织物面内各向异性和非线性材料的特点，分别为在INP文件添加关键词“＊Fabric”和相关代码，或编写用户子程序“VFabric”，这两种方法只是功能和实现形式上的区别，本文采用前一种方法，现简述其本构关系.以图2所示纬向拉伸曲线为例，用分段线性等效处理该非线性曲线，即在每条拉伸曲线上选取n个点，将其近似为n-1条直线相连接，则当织物纬向伸长处于第i（1≤i≤n-1）段时，材料响应视为纬向拉伸模量为Ei的线弹性材料，以此反映织物纬向拉伸非线性.在INP文件中加入以下字段，以建立织物某个方向（以纬向为例）拉伸性能的本构关系.

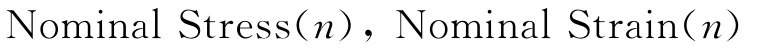
以上字段中，n对名义应力／应变数据直接由图2的拉伸曲线换算得到.在ABAQUS 6.9软件中，利用“＊Fabric”可方便地建立非线弹性、弹塑性、应变率效应等多种薄壳材料模型，但在使用中要注意建立局部坐标系来确定方向.

在INP文件中，由于“＊Fabric”在材料失效时无法实现单元的实时删除，本文使用ABAQUS用户子程序“VUSDFLD”（代码略）来模拟材料失效，失效准则原理为根据织物在经、纬及45°方向上的最大应变来判断单元是否失效.如果单元在某方向上的应变大于该方向上的最大应变，则直接删除该单元.

宏观模型交互原理如图3所示，先采用ABAQUS 6.9软件前处理部分建立几何模型，然后通过ABAQUS 6.9软件的EXPLICIT显式动力学求解器调用“＊Fabric”进行有限元模拟计算，将计算结果中的材料应变传入子程序“VUSDFLD”来控制材料响应和失效，后处理部分则对应力、应变等信息进行采集和输出.

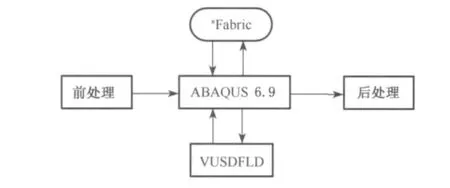
图3 宏观模型交互原理示意图Fig.3 Interaction between subroutine and ABAQUS of the macroscopic model

1.2 模型基本参数及设置

表1和图4分别给出了宏观模型的主要参数和示意图.织物厚度为0.8 mm，边界采用PINNED（U x＝U y＝Uz＝0，U x，U y，U z分别表示x，y，z方向上的位移）方式固定.球形弹子施以z轴正方向以恒定速度顶向织物，弹子与织物间摩擦因数设为0.1.

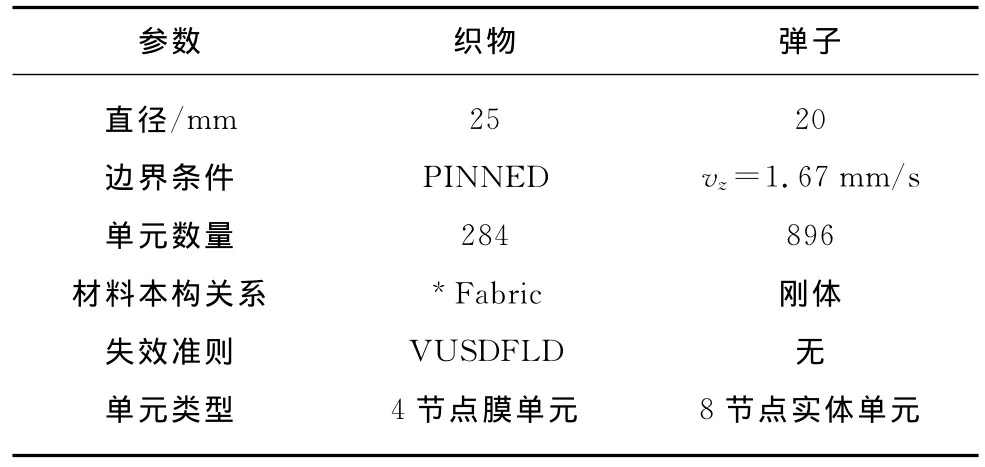
表1 宏观模型主要参数Table 1 Parameters of the macroscopic model

图4 宏观模型示意图Fig.4 Diagram of macroscopic model

2 机织物顶破细观有限元模型

根据图1所示的机织物试样的几何尺寸，建立如图5所示的细观有限元模型，由于纬纱屈曲较小，模型中将其简化为直线；纱线截面设为椭圆形；经、纬纱材料选择各向同性线弹性体，材料失效采用拉伸强度控制.细观模型主要参数如表2所示.另外，纱线之间、弹子与纱线之间的摩擦因数均设为0.1.细观模型中球形弹子部分与宏观模型中的相同.

图5 细观模型示意图Fig.5 Diagram of mesoscopic model

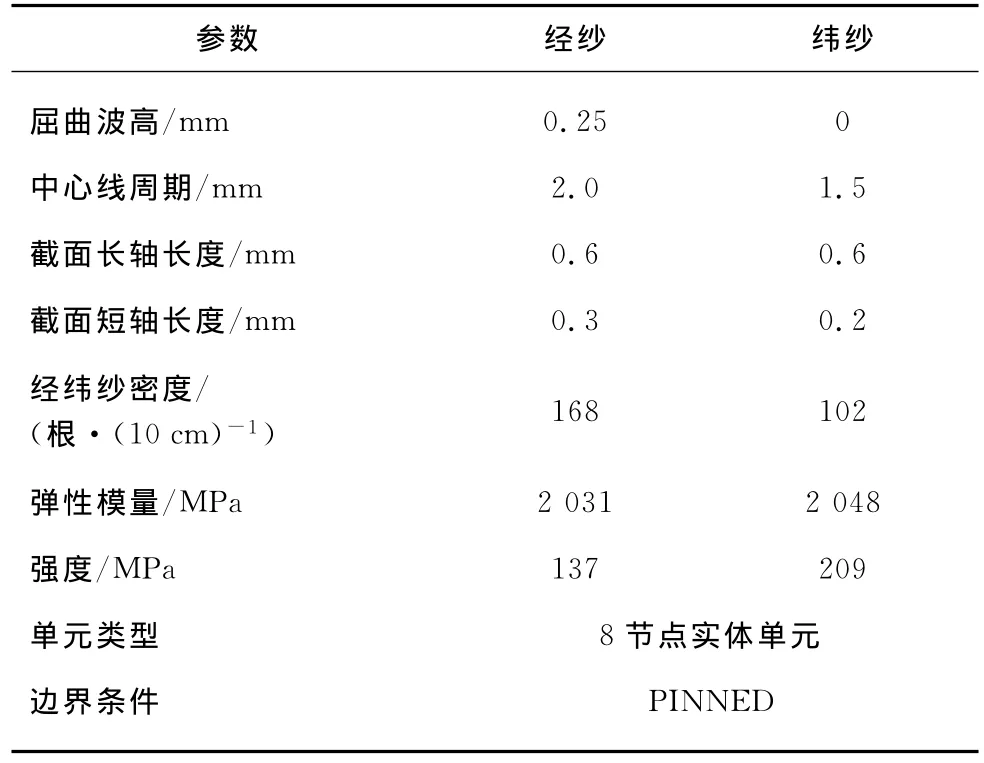
表2 细观模型主要参数Table 2 Parameters of the mesoscopic model

3 试验和模拟结果对比

试验在织物顶破仪（HD026N型）上进行，图6所示为织物的破坏形态（水平方向为纬向）.由图6可以看到，宏、细观模型的模拟结果均与试验结果吻合较好.此外，宏观模型计算耗时较细观模型减少约90%，但只能从织物整体的角度预测织物破坏情况，无法体现织物顶破的细节.图7所示为织物顶破试验及有限元模型（FEM）模拟下的力／位移曲线.由图7可以看到，宏观模型与试验结果吻合程度较细观模型低，这可能是由于忽略了纱线之间的相互作用所导致.另外，细观模型能够模拟力值下降阶段由于纱线断裂的不同时而引起力的波动.

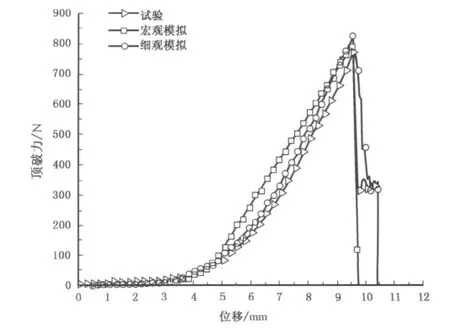
图7 织物顶破试验及FEM模拟下的力／位移曲线Fig.7 Bursting load／displacement of experiment and FEA simulation

4 模型应用与讨论

4.1 顶破过程

本文所建立的有限元模型可方便地分析织物顶破过程中的应力应变情况.图8所示为宏观模型在不同顶破位移s下的主应力和主应变分布.由图8可知，织物主应力集中在经向，且随着顶破位移的增大，经向固定端产生应力集中；织物主应变集中在球形弹子接触的中心区域，当主应变达到失效最大应变时，中心区域先发生破坏.由于应力集中在经向固定端，导致破坏沿经向延伸.由此可知，织物顶破模拟过程中，材料主应变分布决定着破坏区域产生的位置，而主应力分布则决定了破坏的延伸方向.

图9所示为细观模型在不同顶破位移下织物的变形.由图9可看出，机织物顶破可分为纱线伸直、纱线滑移、纱线断裂、破坏延伸4个阶段.对于本文所选的织物试样，经纱屈曲较大，在顶破过程中逐渐伸直，继而经、纬纱发生滑移，纱线间空隙增大；纬纱几乎没有屈曲，在顶破过程中应变较经纱大，当顶破位移为9.7 mm时，纬纱首先断裂，然后裂口沿经向迅速扩大.

4.2 顶破过程中的能量转化

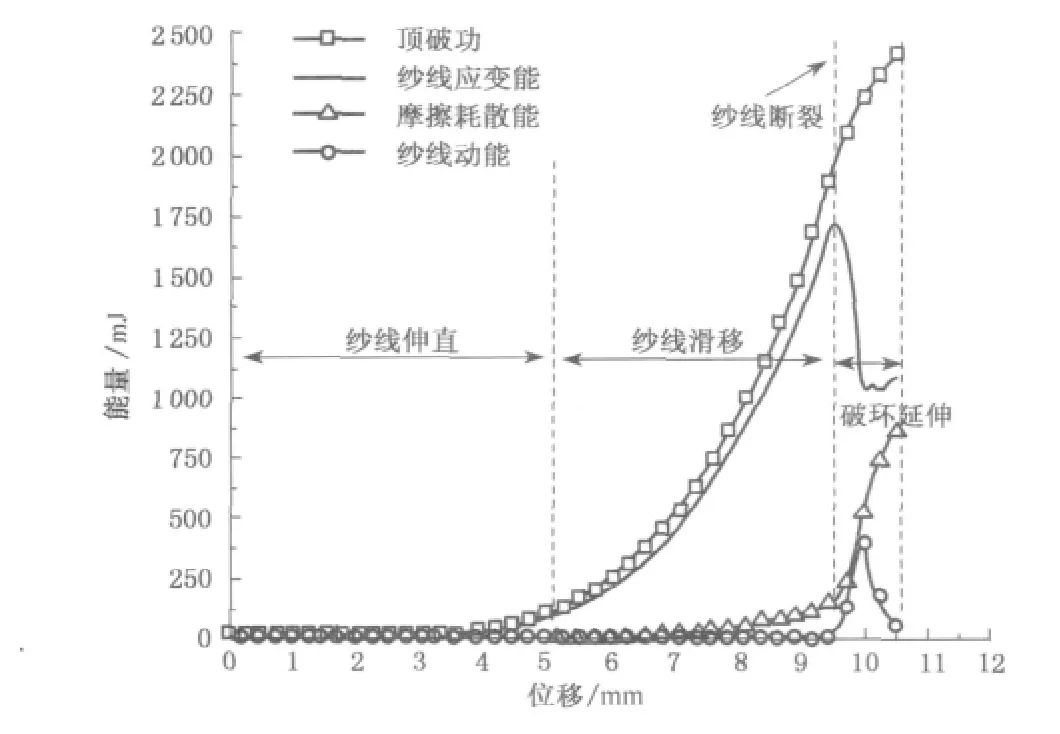
图10 细观模型顶破过程能量的变化Fig.10 Energy transformation during bursting by the mesoscopic model

图10给出了细观模型模拟得出的顶破功、纱线应变能、摩擦耗散能及纱线动能在顶破过程中的变化情况.由图10可看出，在纱线伸直阶段，纱线应变能是外力做功的主要能量转化形式；在纱线滑移阶段，摩擦耗散能逐渐增大；在纱线断裂和破坏延伸阶段，纱线发生回弹，应变能部分转变为纱线动能，同时纱线之间、纱线与弹子之间的滑移导致摩擦耗散能增大.

4.3 摩擦作用对顶破性能的影响

在织物材料、结构一定的情况下，用细观模型模拟了摩擦因数μ分别为0，0.1，0.5情况下织物的顶破过程，其顶破力／位移曲线如图11所示，其中μ＝0.1接近于实际情况.由图11可知，摩擦因数增大，顶破力峰值增大，且峰值出现的位置延后.图12从能量角度解释摩擦因数对顶破过程的影响.由图12可知，摩擦因数增大，织物吸收的应变能上升，对应的摩擦耗散能也上升.

图11 细观模型不同摩擦因数下的顶破力／位移曲线Fig.11 Bursting load／displacement curves with different friction coefficients of mesoscopic model

在不同摩擦因数下宏观和细观模型的破坏形态与主应变的关系如图13所示.由图13（a）可以看出，随着摩擦因数的增大，纱线之间的滑移减弱，织物表面空隙减小.结合图11和12分析可知，纱线间相对滑动的减小，有利于纱线平均分担织物顶破过程中产生的纱线应变，使织物在顶破过程中能够将更多的顶破功转化为纱线应变能，由此机织物的顶破性能得以提升.由图13（a）和13（c）的模拟结果可知，μ＝0.5时，织物破坏位置沿纬向偏移至固定端.这一现象与图13（d）的模拟结果相吻合.观察图13（b）可以看出，在μ＝0.5时，主应变较大的区域不再集中在中心区域，而是趋向外环.这是由于在摩擦作用下，织物与弹子接触的中心区域难以通过相对滑动来传递应变，导致织物中心区域主应变较外环小，从而使得顶破位置发生了上述变化.

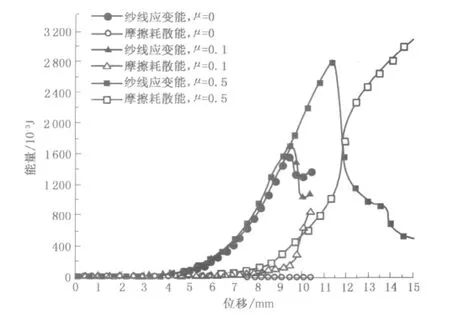
图13 不同摩擦系数下宏观和细观模型的破坏形态与主应变的关系Fig.13 Fracture shape and principal strain of the mesoscopic and macroscopic models under different friction coefficients

由于摩擦作用包括纱线之间及织物与弹子之间两部分，因而需要确定哪部分摩擦作用导致顶破力以及破坏位置的变化.图14所示为μ＝0.5时的宏观和细观模型模拟所得的力／位移曲线.由图14可知，两种模型模拟所得的力／位移曲线较接近.另外，由图13可知，各摩擦因数下织物的宏观和细观模拟破坏形态相似，而宏观模型忽略了纱线之间的相互作用，因而可以推断织物与球形弹子之间的摩擦作用是影响顶破强力和破坏位置的主要原因.因此，可以通过增加机织物与顶破物体之间的摩擦效应来提高织物耐顶破性.延伸阶段.顶破发生前，纱线应变能是主要的能量转化方式；纱线断裂后，纱线回弹现象使部分应变能转化为摩擦耗散能和纱线动能.

随着纱线与弹子之间摩擦作用的增大，顶破过程中纱线之间滑移减少，织物顶破位置由中心区域转移至边缘固定端处，织物应变能和摩擦耗散能增大，进而显著提高机织物的顶破性能.

5 结 语

采用宏观有限元建模方法能简单、快捷地预测机织物的顶破性能.该方法从织物整体角度出发，反映机织物顶破过程中的破坏形态和应力、应变的分布.研究结果表明，织物的主应变分布决定了顶破产生的位置；主应力分布决定了破坏延伸的方向.

细观模型从纱线的角度模拟顶破过程，可将机织物顶破分为纱线伸直、纱线滑移、纱线断裂、破坏

［1］ASTM D 3787—2001，纺织物顶破强力的标准试验方法［S］.

［2］TAYLOR W J，VINSON J R.Modeling ballistic impact into flexible materials［J］.American Institute of Aeronautics and Astronautics Journal，1990，28（12）：2098-2103.

［3］TABIEI A，IVANOV I.Computational micro-mechanical model of flexible woven fabric for finite element impact simulation［J］.Int J Numer Meth Eng，2002，53（6）：1259-1276.

［4］ROYLANCE D.Penetration mechanics of textile structures［M］.New York：Elsevier，1980：273-293.

［5］BILLON H H，ROBINSON D J.Models for the ballistic impact of fabric armour［J］.International Journal of Impact Engineering，2001，25（4）：411-422.

［6］TARFAOUI M，AKESBI S.A finite element model of mechanical properties of plain weave［J］.Colloids and surfaces A：Physicochemical and Engineering Aspects，2001，187：439-448.

［7］HAYHURST C J，HIERMAIER S J，CLEGG R A，et al.Development of material models for Nextel and Kevlar-Epoxy for high pressures and strain rates［J］.International Journal of Impact Engineering，1999，23（1）：365-376.

［8］DUAN Y，KEEFE M，BOGETTI T A，et al.Modeling friction effects on the ballistic impact behavior of a single-ply high-strength fabric ［J］.International Journal of Impact Engineering，2005，31（8）：996-1012.

［9］RAO M P，DUAN Y，KEEFE M，et al.Modeling the effects of yarn material properties and friction on the ballistic impact of a plain-weave fabric［J］.Composite Structures，2009，89（4）：556-566.

Research on Bursting Behaviours of Woven Fabrics by Finite Element Analysis Method

ZHANGTian-yanga，DING Xina，b

（a.College of Textiles；b.Key Laboratory of Textile Science ＆Technology，Ministry of Education，Donghua University，Shanghai 201620，China）

The finite element analysis code ABAQUS is used to simulate the bursting process of woven fabric.Macroscopic and mesoscopic modeling approaches are adopted to analyse the energy absorption mechanism，stress and strain distribution and friction effect during bursting process respectively.It is shown that the macroscopic modeling approach can predict bursting performance easily and quickly.The mesoscopic modeling approach can simulate more detail of the bursting process by identifying yarn stretching，slipping，breaking and rupture during the process.The simulation result shows that damage position depends on the principal strain distribution of the fabric while the crack direction on the principal stress distribution.The yarn strain energy is the dominant energy form before bursting rupture.The energy is partly transformed into yarn kinetic energy and friction dissipation once yarn rupture takes place.In addition，bursting performance can be significantly enhanced if the friction between the fabric and bursting head is increased.

woven fabric；bursting；finite element analysis；model；energy transformation；friction

TS 181；J 523.1

A

2011-09-15

张天阳（1987—），男，内蒙古赤峰人，硕士，研究方向为织物冲击的有限元模拟与分析.E-mail：zhangtianyang＠mail.dhu.edu.cn

丁 辛（联系人），男，教授，E-mail：xding＠dhu.edu.cn

1671-0444（2012）06-0688-07