汽车离合器高强度波形片成形回弹数值模拟及模具优化

张 驰，胡应存，梁宝钱，楚海宾，袁晓明

(1.重庆理工大学材料科学与工程学院，重庆 400054;2.上海交通大学机械与动力工程学院，上海 200234;3.上海萨克斯动力总成部件系统有限公司，上海 201708)

从线性、非线性角度分析传统的冲压成形，其包括接触非线性(各材料之间的摩擦接触导致的非线性)、材料非线性(即弹塑性变形)和几何非线性(大变形、大转动和大位移)三大典型复杂非线性问题［1］。因此板料拉深成形以及模具卸载后的回弹问题难以用传统的方法加以分析和研究。尤其是在高强度弹簧钢的拉深中，回弹现象尤为严重［2］。近年来，汽车离合器波形片广泛采用高强度弹簧钢，且精度要求高，在变形时弹性变形很大，而塑性变形很小，设计模具时，给回弹的预测带来了很大困难。此外，由于该产品成形时既有各类非线性问题，又要考虑弹性及塑性变形，力学分析和有限元分析都具有一定的复杂性，因此对该类零件材料进行深入分析和探究显得非常必要。

本文从有限元模型的单元类型及屈服模型、材料塑性本构模型拟合等方面进行研究，利用高级非线性有限元分析软件MSC.Marc对某汽车离合器高强度波形片的回弹进行数值模拟，并对比生产产品，以验证该分析技术的可靠性。

1 Barlat各向异性屈服准则

因汽车波形片所用材料为1 mm左右的薄钢板，原材料经轧制生产后，各向异性现象非常明显，所以必须选用能正确反映该类板料特性的材料模型。Hill［3］在 1948 年提出了 Hill’48 各向异性屈服准则。此准则方程简捷，采用3个不同角度的厚向异性参数r0、r45和r90表示板料的各项异性属性，而且厚向异性参数非常容易用单向拉深试验得到，很多有限元系统都采用了该方法。研究表明该准则在各项异性现象非常明显的(r＞1)材料中比较准确［4］。Lian 和 Barlat［5］在 1989 年又提出了一个更加准确地表达板类材料各向异性的准则条件，该准则与基于结晶学计算的屈服面保持了很好的一致性。已经有很多分析表明该准则能较好地描述各向异性板类材料的屈服行为及板料成形之后的回弹。Barlat等［6－8］在 1991、1997及2003年又提出了一些更能准确描述各向异性的新准则，但此类表达式需要的参数及试验相对比较繁琐。因此在模拟软件中Barlat’89和Hill’48得到了很好的应用。

Barlat’89各向异性屈服准则的屈服方程为

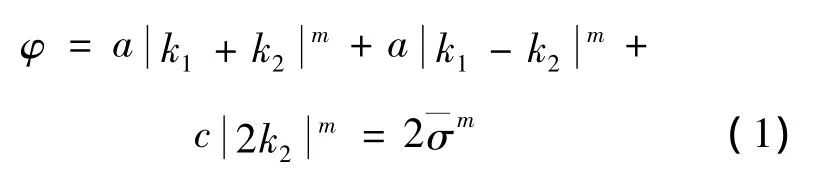
其中:

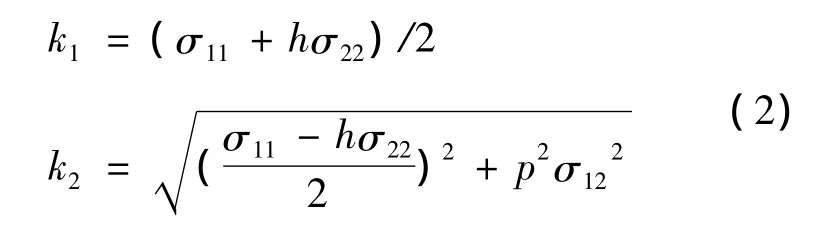
m为屈服方程指数，它跟晶体结构相关，当材料晶体结构为Body-Centered Cubic(体心立方)时，m=6;当材料晶体结构为Face-Centered Cubic(面心立方)时，m=8。在m为定值的情况下，4个材料常数h、c、a及p均为独立常数，到目前为止分别有2种方法来计算［3］。

第1种方法:

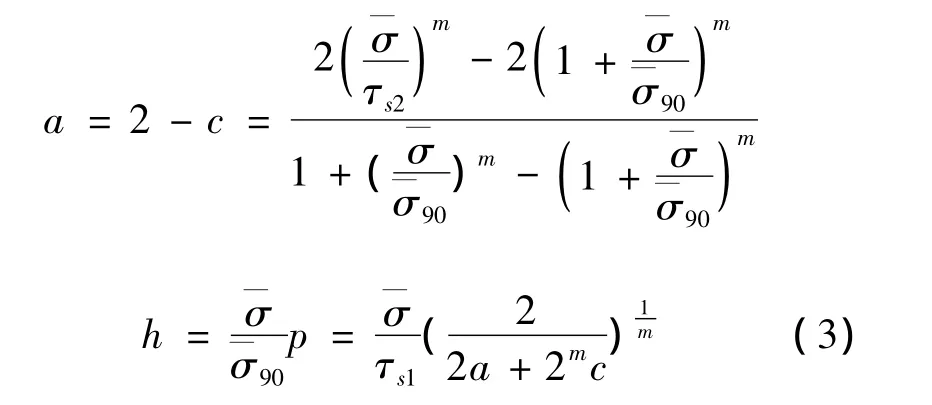
第2种方法:

3 个材料参数 p、h 及 a 由 r0、r45、r90(Lankford’s常数)确定。本文采用此方法。

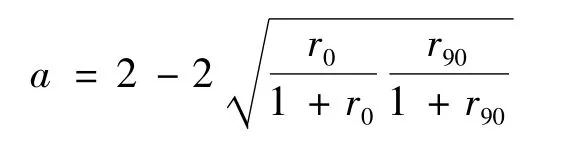
材料参数p需要通过微分方程迭代计算，在单向拉伸试验条件下，已知a、c，存在rθ与参数p之间的关系。很多研究分析说明，在θ=45°时，rθ为参数p的递增函数，经式(5)迭代计算可求得参数p。

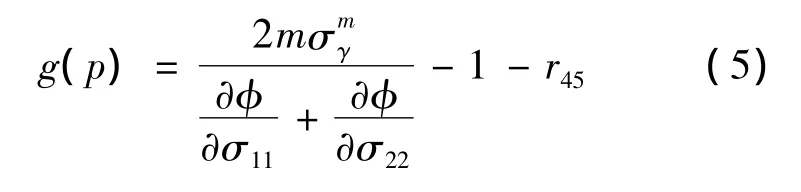
2 汽车离合器波形片结构工艺及材料属性参数

图1为某型号的汽车离合器波形片。该波形片产品高度低，板料尺寸在成形回弹后变化小。板料材料为65Mn，含碳量约0.65%，属于高强度弹簧钢，料厚0.6 mm。材料屈强比小，塑性很小，硬度较高，材料的屈服强度与抗拉强度分别达到1 300 MPa和1 600 MPa，成形性能差。结合工厂条件和生产批量，此波形片的成形工艺为:第1道工艺，冲孔落料;第2道工艺，冲压成形。

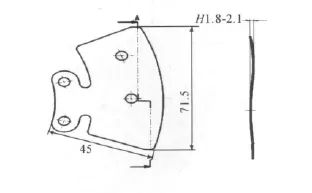
图1 某公司型号的汽车离合器波形片

板料的拉伸试验研究分析是对材料力学性能测试的基本常用试验。本文也是严格按照国家标准金属材料室温拉伸试验方法(GBT228—2002)、金属薄板和薄带塑性应变比(r值)的测定(GB/T5027—2007)以及金属薄板和薄带拉伸应变硬化指数(n值)试验方法(GBT 5028—2008)进行拉伸试验，并对试验数据进行处理，将工程应力应变曲线转化为真实应力应变曲线，应用最小二乘法原理拟合得到板料的性能参数。材料拉伸试验设备为万能拉伸试验机。拉伸试验得到的真实应力应变曲线如图2所示，得到的材料参数如表1所示。

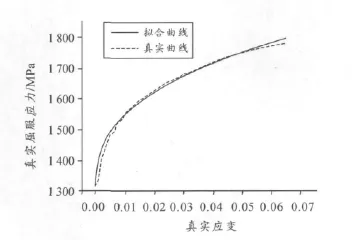
图2 真实应力应变曲线与模拟拟合曲线比较

经最小二乘法拟合后，材料的屈服应力应变的数学本构方程为

复相关系数R为0.993 54，因此线性回归效果非常好，试验得到的真实应力应变曲线与拟合的本构模型方程比较(如图2所示)，也证明了该本构模型与实际曲线的接近程度高。

表1 高强钢材料属性参数

3 MSC.Marc回弹数值模拟及模具优化

模拟凸模速度取0.05 m/s，成形时不考虑重力，采用Marc自带的185号实体壳单元。上模和下模设置为刚性体，坯料设置为变形体。模具与坯料之间的摩擦接触选用双线性摩擦，其摩擦系数根据经验确定为0.1。选用修正的拉格朗日法(updated Largrange procudure)来分析模拟金属的材料弯曲成形过程。收敛准则采用位移判断标准，容差1%。模拟回弹时，释放工件与模具之间的接触。材料应力应变本构及参数采用式(6)模型和表1数据。

根据回弹理论，计算确定上下模具的成形尺寸，模拟的几何模型如图3所示。

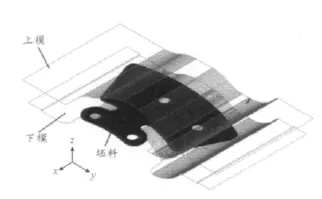
图3 模拟的几何模型

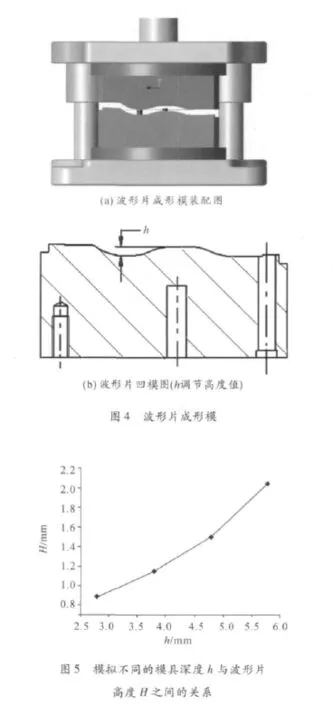
图1中的波形片回弹后的高度值H是评价其是否合格的重要指标，设计波形片高度H值要求在1.8～2.1 mm。按照传统模具设计方式，考虑回弹因素，一般采用在模具中加回弹余量进行修改设计的方式，即设计模具的实际深度为要求高度H外加回弹余量。高强度波形片成形回弹量大，按照传统的经验公式来计算高强度的波形片回弹量比较困难，从而会影响产品精度和生产效率;另外，通过试模方式来调整，这需要多次试模，然后修改模具，以满足产品的技术要求，其模具设计及制造周期长(波形片成形模如图4所示)。通过高级非线性有限元来模拟高强度波形片成形的回弹，将其结果用来进行模具优化，是精确预测回弹的一种高效方式。

为比较不同的模具深度h与成形回弹后的零件高度H之间的关系，通过有限元模拟分析得到两者之间的关系，如图5所示。可以发现，当模具深度h=2.8 mm时，模拟计算得到的零件回弹后高度H为0.88 mm。随着凹模深度h的增加，钢板的变形量增大，波形片回弹量减小，因此波形片高度H也随之增加。当模拟的模具深度h在5.35～5.9 mm时，模拟的产品高度 H在1.8～2.05 mm，符合产品设计要求。

根据模拟结果，笔者设计凹模深度 h=5.8 mm(波形片成形模实物如图6所示)。成形后，经过对产品实物(如图7所示)测试，得到了波形片的高度H为1.93 mm。它满足产品的使用要求，其模拟结果与实际试验结果之间吻合较好(如图8所示)，因此很好地发挥了有限元数值模拟技术指导模具设计的作用，模具设计成本得到了有效控制，研究和开发周期也大大缩短。

4 结论

1)采用Balart材料屈服准则准确描述了高强刚板料各向异性，可以很好地反映材料属性。

2)在有限元计算中，应用实体壳单元理论研究分析薄板类材料的冲压成形及回弹，与三维实体单元相比，其计算效率明显提高，且保持了良好的精度。

3)在有限元分析模型中，采用修正的拉格朗日法(updated Largrange procudure)，可以适用于增量类型的本构关系的大变形问题，如薄板材料的弹塑性大变形问题。

4)轧制薄板料成形后的卸载回弹过程采用逐步释放成形应力，以及采取模具与工件逐步分离的方式，可以有效地模拟分析板料实际回弹卸载过程。

［1］钟志华，李光耀.薄板冲压成型过程的计算机仿真与应用［M］.北京:北京理工大学出版社，1998.

［2］朱东坡，孙琨.板料成形回弹问题研究新进展［J］.塑性工程学报，2000(7):11－15.

［3］Hill R.Theoretical plasticity of textured aggregates［J］.Math Proc Camb Phil Soc，1948，85:179.

［4］Woodthorpe J，Pearce R.Effect of R and N opinion the forming limit diagrams of sheet steel［J］.Sheet Meatl Ind，1969，46(12):1061 －1067.

［5］Barlat F，Lian J.Plastic behavior and stretchability of sheet metals Part I:a yield function for orthotropic sheets under plane stress conditions［J］.International Journal of Plasticity，1989，5:51 －66.

［6］Barlat F，Daniel J L，John C B.A six-component yield function for anisotropic materials［J］.International Journal of Plasticity，1991，7:693 －712.

［7］Barlat F，Becker R C，Hayashida Y，et al.Yielding description for solution strengthened aluminum alloys［J］.International Journal of Plasticity，1997，13(4):385－401.

［8］Barlat F，Brem J C，Yoon J W，et al.Plane stress yield function for aluminum alloy sheets ― part 1:theory［J］.International Journal of Plasticity，2003，19:1297 －1319.