求解电磁波在层状有耗介质中反射和透射的精细积分方法

方 宏 远， 林 皋＊， 张 蓓

（1.大连理工大学 建设工程学部 土木工程学院，辽宁 大连 116024；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；3.郑州大学 水利与环境学院，河南 郑州 450002）

0 引 言

近年来，电磁无损检测技术被广泛应用于各个工程领域.很多工程结构，比如道路、隧道等，都是层状体系，利用电磁波对这些工程结构进行无损探测都可以归结为电磁波在层状体系中的传播问题.分析电磁波在层状介质中的反射与透射，常采用传递矩阵方法[1]，但大部分工程材料都属于有耗介质，采用该方法计算有耗层状体系，如果材料电导率比较大或者结构层数比较多，容易出现数值失稳问题，导致计算结果发散.

精细积分方法[2]是一种高精度且无条件稳定[2]的数值算法，很适合求解层状体系中电磁波的反射和透射问题.为了避免出现传递矩阵方法中指数矩阵相乘的问题，可采用基于两端边值问题的精细积分方法，将控制方程按边值问题进行计算，从而避免了在计算过程中出现指数增大的情况，可以保持数值结果的精度和稳定性.

1 控制方程的推导[1，3]

不失一般性，文中介质按各向异性考虑.此时，频域麦克斯韦方程组可以表述为

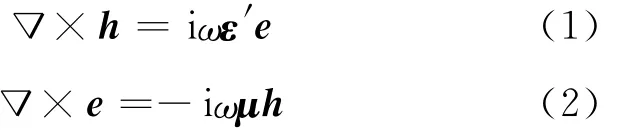
式中：h表示磁场向量；e表示电场向量；μ为磁导率；ε′为复介电常数，ε′＝ε＋σ/iω，其中ε是介电常数，σ是电导率.各向异性介质中μ、ε′均为二阶张量.

由电磁场理论可知，在两种介质界面处，电场和磁场的水平分量连续.为了便于在分层界面上匹配边界条件，可将旋度算子和场量按下式进行分解：

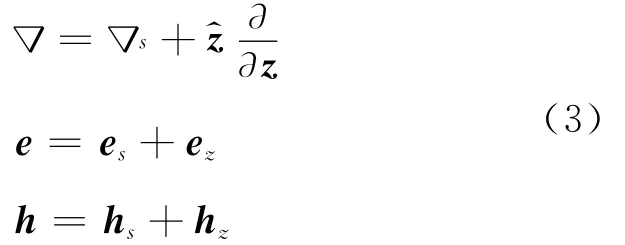
式中：下标s代表场量的水平分量x、y，下标z表示场量的垂直分量.z＾表示z方向的单位矢量.则相应的本构参数变为

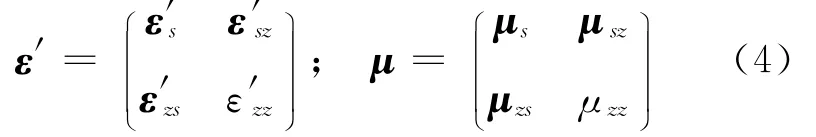
式中：ε′s、μs是2×2的矩阵，ε′sz、μsz是2×1的矩阵，ε′zs、μzs是1×2的矩阵.

将式（3）、（4）代入式（1）、（2）整理可得

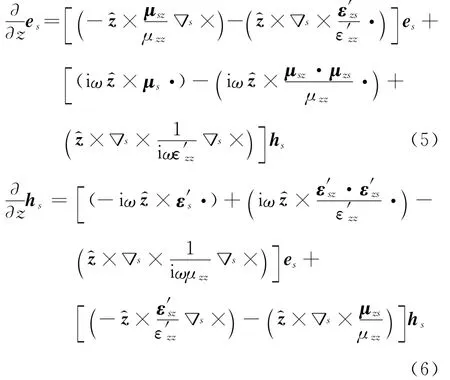
电场和磁场的频域列式可以写为

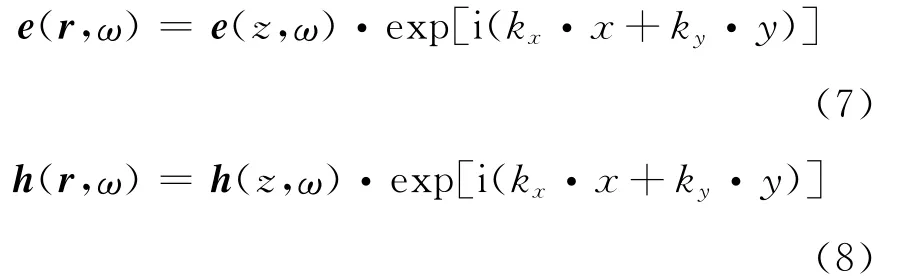
将式（7）、（8）代入式（5）、（6），控制方程可以写为

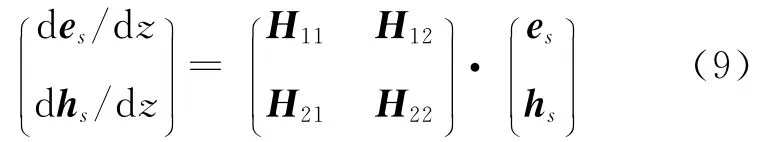
式中：es＝ （exey）T，hs＝ （hxhy）T，H11、H12、H21、H22均为2×2的矩阵.

2 基于两端边值问题的精细积分方法[4－7]

精细积分是求解一阶常微分方程的高精度算法，已被应用于结构动力分析、控制论、波导等诸多领域.该方法通过将原有积分步长再细分为2N个等长的微段，对于微段的层间矩阵利用幂级数展开求解.可以证明级数展开的截断误差低于计算机的舍入误差，从而得到几乎是计算机字长上精确的数值解.并利用结构力学中的多层子结构算法对这些微段进行合并消元，在保证数值结果精度的前提下，大大提高了运算效率.

边值问题精细积分方法并没有采用传统的差分格式对控制方程（9）进行离散求解.对于线性系统中任意区段[za，zb]，两端处电场和磁场的关系一定可以表示为

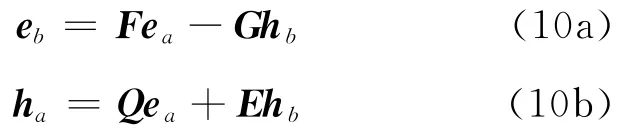
式中：ea、eb、ha、hb分别表示两端的电场和磁场向量.E、F、G、Q为待求的2×2矩阵，均为za、zb的函数.

将方程（10）对zb求导可得

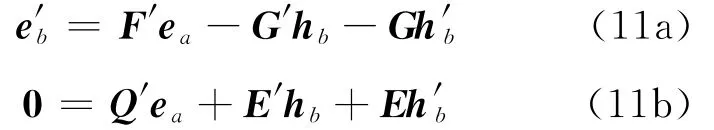
在z＝zb处状态方程（9）可以写为

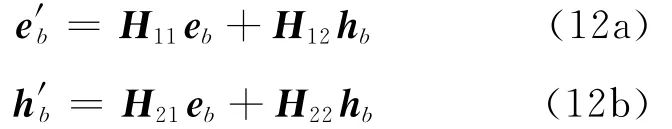
联立方程（10）～ （12）可得

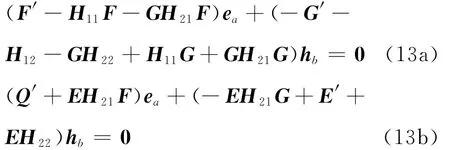
其中ea、hb可看作独立无关的任意向量，所以有

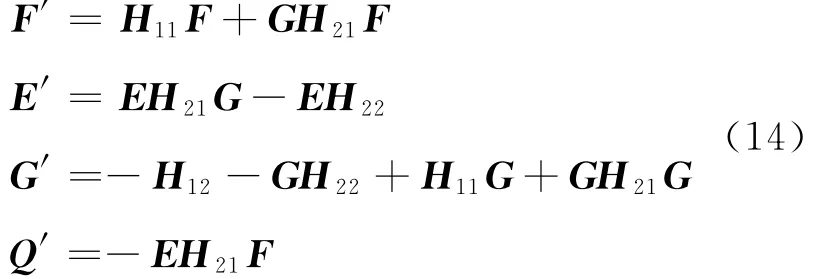
当za趋近于zb时，有边界条件

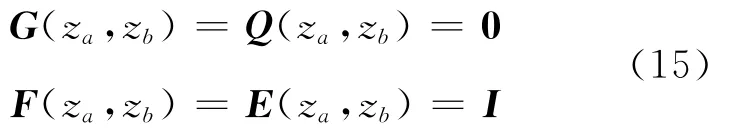
2.1 区段方程的合并

对于相邻两区段[za，zb]、[zb，zc]，分别应用方程（10）可以得到

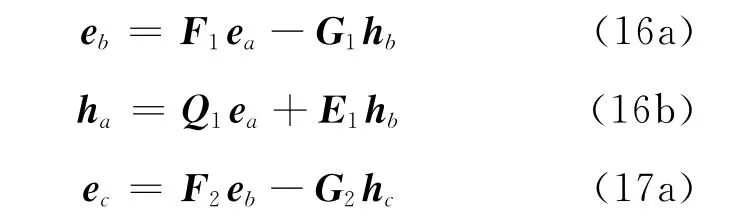
对于合并后的区段[za，zc]，应用方程（10）可以得到

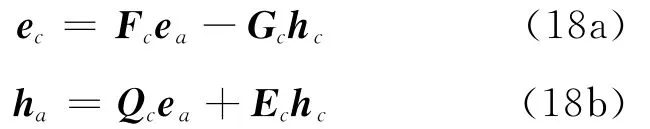
将方程（17b）代入方程（16a）求出

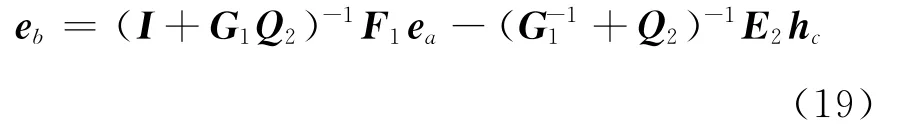
将方程（16a）代入方程（17b）得

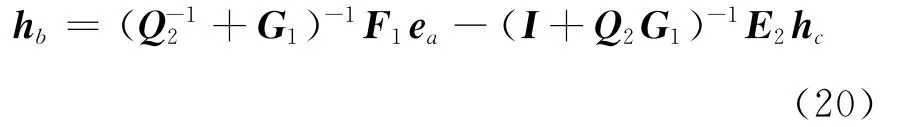
将方程（19）、（20）代入式（16b）、（18a）整理可得

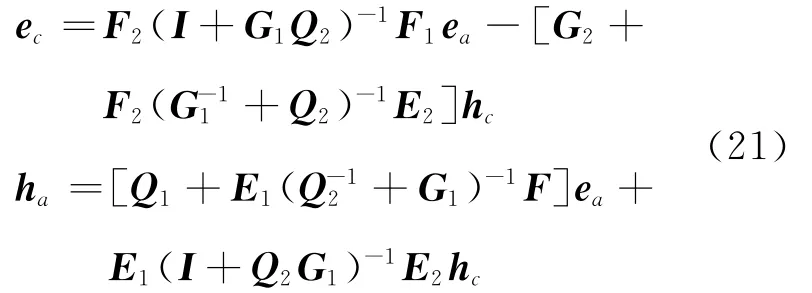
对比方程（18）和（21）可得

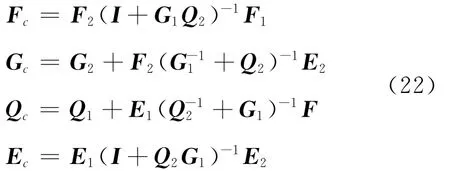
2.2 区段矩阵E、F、G、Q的计算（2 N 类算法）

对于任意一层i，厚度为hi，将其划分为等长的2N个小区间，N可以取得很大，例如20.由于间隔非常小，区段矩阵E、F、G、Q可按幂级数展开加以表示，并令τ＝hi/2N.当τ足够小时，幂级数取4项，截断误差已经很小了.

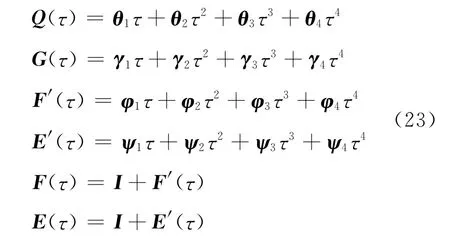
式中：θi、γi、φi、ψi（i＝1，2，3，4）均为2×2矩阵，I为2×2单位矩阵.

将方程（23）代入方程（14），对比左右端项可得

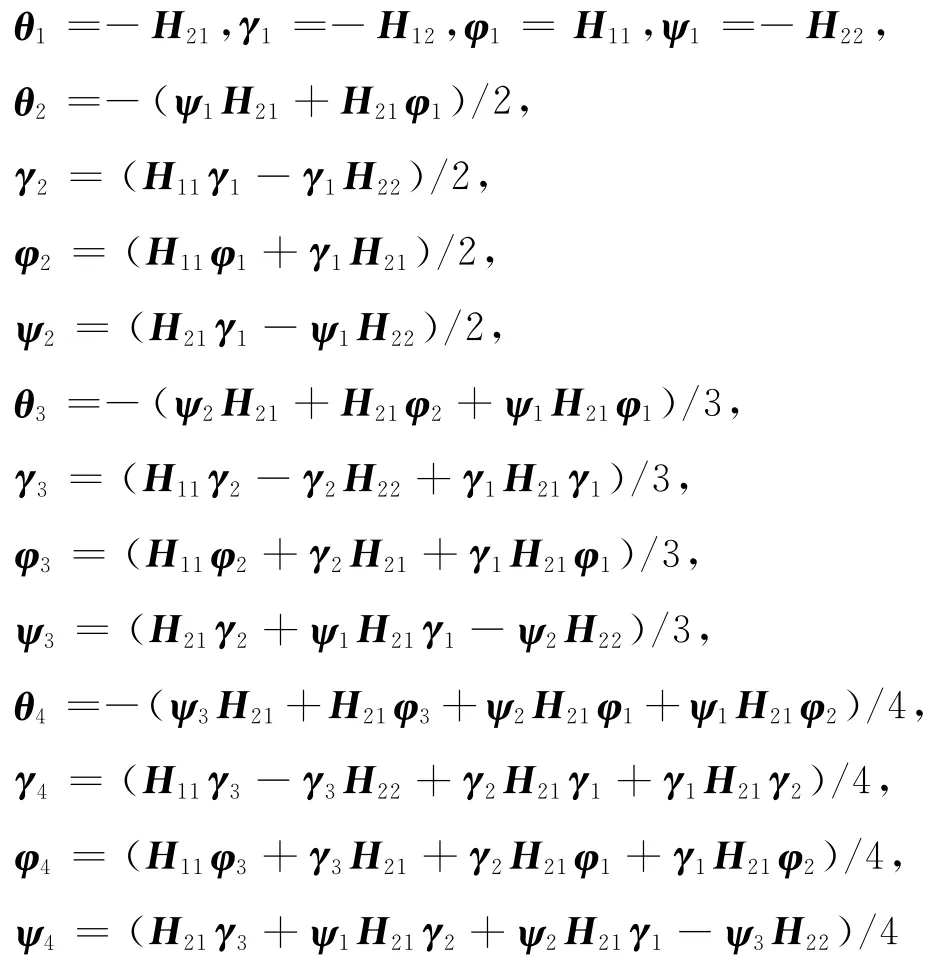
这里需要注意的是，τ特别小，导致F′（τ）、E′（τ）特别小，如果直接将其与单位阵相加的话，会导致计算精度丧失，所以不能直接利用式（22）进行组合，需改写为以下形式：

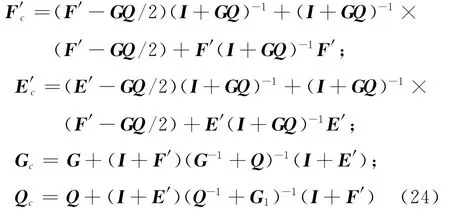
由于同一种介质层内所有区段均相等，采用式（24）消元一次，区段数就会减少一半，经过N次消元后，即可求出这一层的区段矩阵.依此类推可以求得每一介质层的区段矩阵Ei、Fi、Gi、Qi.然后按照式（22）组装整个层状体系的区段矩阵Ec、Fc、Gc、Qc.

3 边界条件的推导

3.1 上部边界条件

层状体系如图1所示，第1层为上部半无限空间，根据电磁场理论，第1层中传播的波可以表述为向上传播的波和向下传播的波两部分.

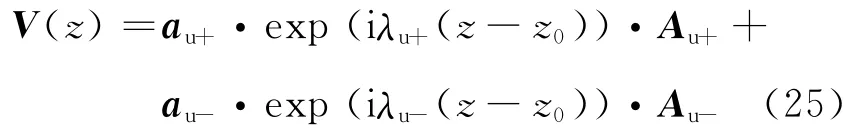
式中：exp （iλu＋（z－z0））＝ diag｛exp （iλu1（zz0））， exp（iλu2（z－z0））｝，λu＋为方程（9）中矩阵H的正特征值，代表上半空间中向上传播的波.exp（iλu－（z－z0））＝diag｛exp （iλu3（z－z0）），exp（iλu4（z－z0））｝，λu－为矩阵H的负特征值，代表上半空间中向下传播的波.au＋＝ （au1au2）、au－＝（au3au4），为特征值相对应的特征向量；Au＋＝（Au1Au2）T、Au－＝ （Au3Au4）T，为 相应幅值；V＝ （exeyhxhy）T，为一四元列矢量.

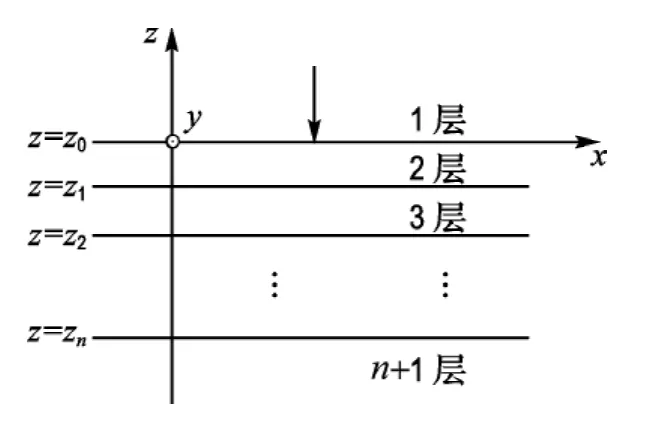
图1 层状体系示意图Fig.1 Sketch of layered system

定义反射系数矩阵R，R＝Au＋/Au－，R为2×2矩阵，式（25）可重写为其中I为2×2单位矩阵.

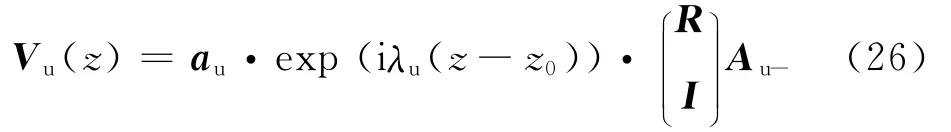
在z＝z0处将上式展开，从而得到上部半空间的边界条件

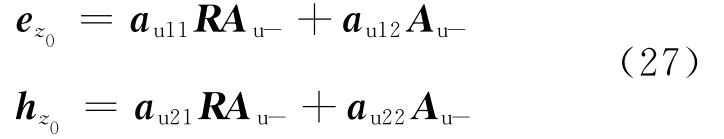
式中au11、au12、au21、au22均为2×2矩阵，可由au分块获得.

3.2 下部边界条件

第n＋1层为下部半无限空间，下部半空间只有向下传播的波，所以

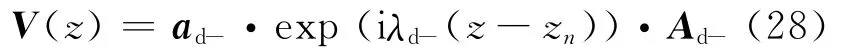
式中：exp （iλd－（z－zn））＝ diag ｛exp （iλd3（zzn）），exp（iλd4（z－zn））｝，λd－为下半空间状态方程中矩阵H的负特征值，代表下半无限空间中向下传播的波.ad－＝ （ad3ad4），Ad－＝ （Ad3Ad4），符号表示与上半空间相同.

定义折射系数矩阵T，T＝Ad－/Au－，T为2×2矩阵.

所以下半空间的波可以写为

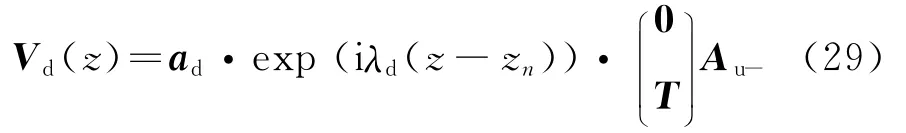
其中0为2×2零矩阵.

在z＝zb处，展开上式可得下半空间的边界条件

将式（27）、（30）代入方程（10），即可求得层状体系的反射系数和折射系数.这里的E、F、G、Q是采用精细积分方法求得的整个层状体系的区段矩阵Ec、Fc、Gc、Qc.

4 数值算例

iωε′，其余元素均为0.其中为电磁波在空气中的传播常数，θ为入射角.设第1层介质介电常数ε1＝9ε0，电导率σ1＝0.05S/m，厚度d1＝0.3m；第2层介质介电常数ε2＝30ε0，电导率σ2＝0.05S/m，为半无限空间.两层介质磁导率均等于真空磁导率，则入射角为0°和30°时，表面反射系数如表1所示.

例2 将例1中第1层介质的电导率σ1变为4.05S/m，其他参数均不变，则垂直入射时，第1层与第2层界面处透射系数如表2所示.

例3 例1中其他参数不变，第1层的介电常数按各向异性考虑，εxx＝9ε0，εxy＝8ε0，εxz＝7ε0，9ε0，εzz＝10ε0，则空气与第1层介质界面处反射系数如表3所示.

例1 均匀平面波由空气入射一个两层体系，设每层介质均为各向同性，空气层的介电常数和磁导率分别为真空中的介电常数和磁导率ε0、μ0.那 么 方 程 （9）中 矩 阵H可 以 简 化 为

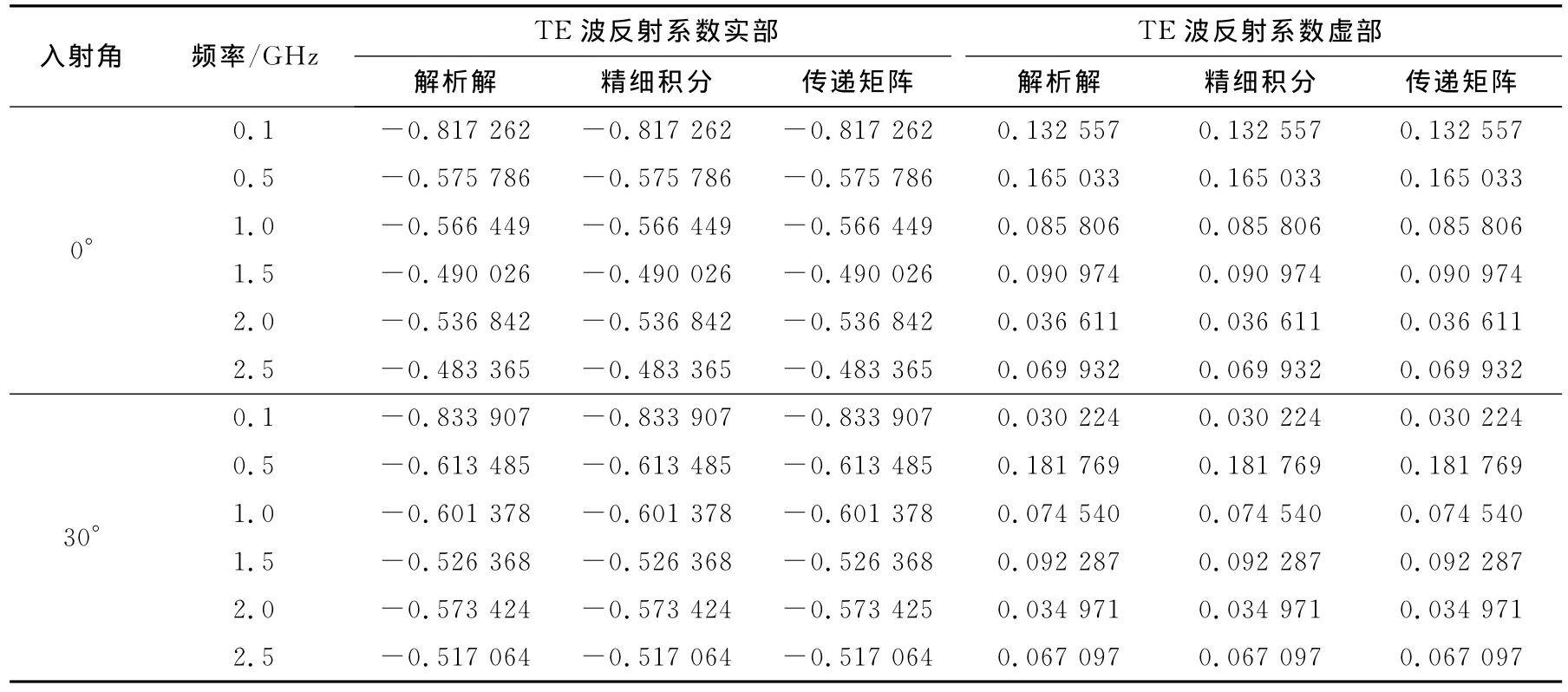
表1 两层体系反射系数对比结果Tab.1 Comparison result of reflection coefficient in two layered medium

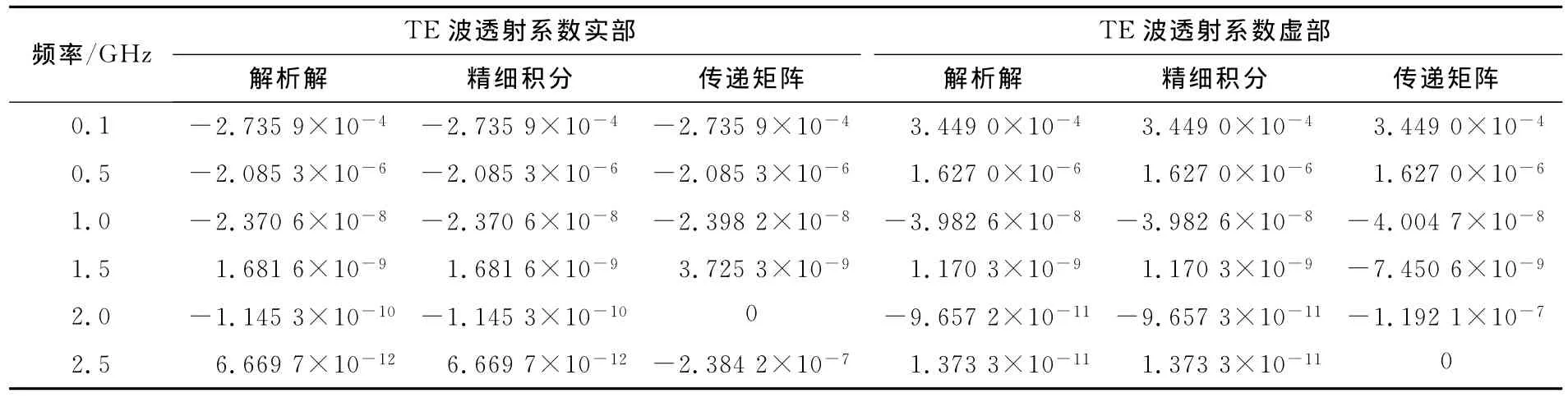
表2 两层体系透射系数对比结果Tab.2 Comparison result of transmission coefficient in two layered medium

表3 各向异性两层体系反射系数Tab.3 Reflection coefficient of two layered anisotropic medium

5 结 论

对比精细积分方法和广义传递矩阵法数值结果可知，对于低耗层状体系，两种方法都能获得精确的结果，但如果介质电导率比较大，广义传递矩阵方法的数值结果就出现了不稳定性.这主要是由于该方法求解结构层总传递矩阵过程是一个指数矩阵相乘的问题，会出现大数溢出的现象，电导率越大，传递矩阵中数值增大的项增长越快，越容易造成数值不稳定.而精细积分方法中所示的层间矩阵合并过程，是一个指数矩阵相除的过程，避免了出现大数溢出的情况，保持了该算法的数值稳定性.利用基于两端边值问题的精细积分方法计算层状体系反射系数和透射系数，具有更高的精度和数值稳定性.

[1] 郑宏兴，葛德彪.广义传播矩阵法分析分层各向异性材料对电磁波的反射与透射[J].物理学报，2000，49（9）：1702－1706.ZHENG Hong－xing，GE De－biao.Electromagnetic wave reflection and transmission of anisotropic layered media by generalized propagation matrix method[J].Acta Physica Sinica，2000，49（9）：1702－1706.（in Chinese）

[2] 赵丽滨，张建宇，王寿梅.精细积分方法的稳定性和精度分析[J].北京航空航天大学学报，2000，26（5）：569－572.ZHAO Li－bin，ZHANG Jian－yu，WANG Shou－mei.Stability and precision analysis for precise integration method [J]. Journal of Beijing University of Aeronautics and Astronautics，2000，26（5）：569－572.（in Chinese）

[3] 周永祖.非均匀介质中的场与波[M].聂在平，柳清伙，译.北京：电子工业出版社，1992.Chew Weng－cho.Waves and Fields in Inhomogeneous Media [M].NIE Zai－ping，LIU Qing－huo，tran.Beijing：Electronic Industry Press， 1992. （in Chinese）

[4] GAO Qiang，ZHONG Wan－xie，Howson W P.A precise method for solving wave propagation problems in layered anisotropic media [J]. Wave Motion，2004，40（3）：191－207.

[5] ZHONG Wan－xie，LIN Jia－hao，GAO Qiang.The precise computation for wave propagation in a stratified materials [J].International Journal for Numerical Methods in Engineering，2004，60（1）：11－25.

[6] GAO Qiang，LIN Jia－hao，ZHONG Wan－xie，etal.A precise numerical method for Rayleigh waves in a stratified half space [J].International Journal for Numerical Methods in Engineering，2006，67（6）：771－786.

[7] ZHONG Wan－xie.Combined method for the solution of asymmetric Riccati differential equations [J].Computer Methods in Applied Mechanics and Engineering，2001，191：93－102