火箭助飞鱼雷海上落点测控系统测量误差分析

张玉涛, 薛 飞, 李 鹏



火箭助飞鱼雷海上落点测控系统测量误差分析

张玉涛, 薛 飞, 李 鹏

(中国人民解放军91439部队, 辽宁 大连, 116041)

火箭助飞鱼雷海上落点是影响其命中精度的重要参数, 在试验测量时, 用于水声定位的海上浮标可能会出现缺失而影响其测量精度。本文利用Matlab软件对火箭助飞鱼雷海上落点测量浮标预设阵型进行了仿真研究, 分析了缺失部分浮标对测量精度的影响, 给出了缺失浮标数量及阵型最低条件, 即当12个浮标中缺失4个浮标且阵型不对称时, 测量精度会迅速下降。研究结果表明, 在落点测控过程中, 如果文中的预设浮标阵型不满足最低条件, 应重新调整浮标。该研究可为海上实际试验指挥决策提供技术支撑。

火箭助飞鱼雷;测量精度; 水声定位; 浮标阵型; 仿真

0 引言

火箭助飞鱼雷发射后在海上的落点散布精度是考核其战技指标的重要参数, 它与鱼雷的作战使用方法、发射平台、系统性能乃至作战海空域自然条件等多方面因素有密切关系。

火箭助飞鱼雷海上落点散布考核由一套基于矢量水听器的被动测量系统进行测量。在海上实施时, 首先布设浮标, 利用浮标携带的矢量水听器完成鱼雷入水击水声的方位估计, 系统显控端分析浮标位置和水听器测角信息后, 确定鱼雷入水点大地坐标。该坐标值与考核指标比对, 完成落点精度考核。本文初步分析了海上预设浮标布阵, 在单个或多个浮标出现海上走锚、通信不畅、性能下降等情况时, 在短暂的鱼雷发射时间窗口内如何保证测量的可靠性和精度, 为试验指挥决策提供依据, 为能否发射鱼雷提供技术支撑。

1 纯方位定位原理

1.1 双浮标阵定位

根据矢量水听器工作原理, 可将纯方位击水声定位归结为图1所示的平面定位问题, 图中,为浮标号,为目标入水点位置。首先对坐标系进行定义: 基线坐标系是以阵元为坐标原点, 阵元和阵元构成的极限为轴, 由到方向为轴正向, 该坐标系称为基线坐标系[x, y],,=1, 2, 3,…,≠。大地坐标系取北地东坐标, 矢量水听器轴方向与正东方向一致,轴方向与正北方向一致。很明显, 利用两浮标定位入水点的问题, 就简化为解算三角形△。

图1 大地坐标系与基线坐标系

定义基线长度为d, 浮标和测得的目标方位角分别为β和β, 大地坐标系与基线坐标系夹角为γ, 且均以顺时针方向为正。α和α分别是△的内角,α,α∈(0,π)。则角度间存在如下关系

在基线坐标系下, 入水点的位置为

1.2 多浮标阵定位

试验实施时, 布放浮标个数必然多于2个, 这样的话入水点在不同基线坐标系下会产生不同测值。为提高定位精度, 用权函数来综合所有基线对入水点的定位结果。

为不失一般性, 以4个浮标组成测量阵为例。浮标1, 2, 3, 4与构成6个三角形, 如图2所示, 在任意一个三角形△下,的坐标由式(2)给出, 其中=12, 23, 34, 41, 13, 24。

基线坐标系的原点在大地坐标系中的位置为(x,y), 由此可知在大地坐标系下入水点的坐标为

其中

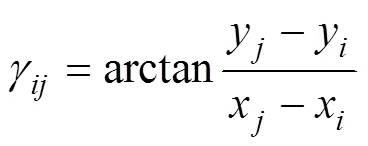
由式(2)及式(3)即可解算入水点的位置。为提高定位精度, 须对解进行误差分析, 得到权函数, 用权函数来综合测量阵所有基线对目标的定位结果。

根据文献[1]可知权函数为误差扩大函数的均方根倒数, 即

对入水点的精确定位结果应为所有基线定位结果的加权综合, 即

其中(kx, ky)由式(3)确定,=12, 23, 34, 41, 13, 24。

2 定位误差传递

根据误差理论, 设1,2,…,x)看成随机变量的函数, 并用,σ1,σ2,…,σ表示,1,2,…,x的标准误差, 则其误差传递公式为

对2个浮标构成的基线坐标系, 目标在其下的坐标由式(2)给出。将其带入式(7)可得到基线坐标系下误差为

其中=π-1-2,1,2∈(0,π)。

试验时, 距离由差分全球定位系统(differ- rence Global Positioning System, DGPS)测出, 测量值的相对误差不足千分之一, 可以认为σ项为小量, 忽略不计。对入水点的定位误差主要由1和2的测量误差产生, 当认为各浮标性能一致时, 可假定其均方误差都相同。同时考虑以往试验结果, 认为在3 km范围内, 测角误差为1°, 则有σ1=σ2=1°。

3 仿真结果及分析

3.1 仿真条件

入水点测量系统共有12个浮标, 为保证测量的可靠性, 海上布设12个浮标, 考虑到鱼雷散布精度, 预设浮标阵型如图3所示, 围绕中心点对称布设12个浮标, 4个置于390 m, 4个置于1 170 m, 4个置于1 650 m。其中单标仿真误差1°。利用MATLAB软件按照预设条件进行仿真计算。

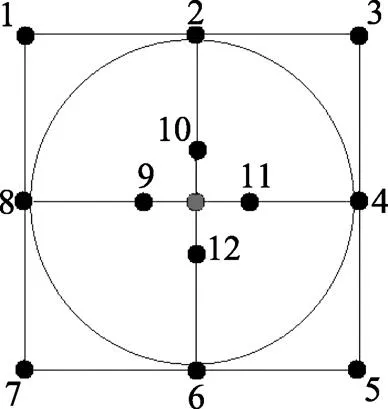
图3 预设浮标阵型

3.2 仿真结果及分析

以式(8)为依据, 设计仿真试验, 对缺少1个浮标、2个浮标、3个浮标、4个浮标及12浮标全工作情况下的入水点测量精度进行分析。

3.2.1 12个浮标全部正常工作

12个浮标全部正常工作时, 误差分布仿真结果如图4所示。由图可见, 浮标误差分布图关于基线有对称性, 越靠近阵中心误差越小, 向外逐渐递增; 阵外一定区域亦有一定精度, 可以利用; 在浮标基线上存在低精度区, 这是因为该区域α,α趋近于零, 式(2)结果发散。

图4 12个浮标全部正常工作时误差分布仿真结果

3.2.2 缺少1个浮标

由于阵型本身的对称性和水声定位的基本原理, 缺失1个浮标情况只讨论内部缺1个、外围中点缺1个和外围顶角缺1个这3种情况。从图5可知, 在缺1浮标时, 精度与图4阵内外精度分布大致相同。

3.2.3 缺少2~3个浮标

类似分析缺失2~3个浮标情况发现, 测阵精度仍可以基本保证, 如图6所示。

3.2.4 缺少4个浮标

缺失4个浮标情况较多, 这里讨论4种典型情况。从图7可见, 当不改变浮标阵对称结构时, 测阵精度尚可保证, 但当破坏了对称性, 出现缺一边或缺一角时, 相应位置精度迅速下降。

图5 缺少1个浮标时误差分布仿真结果

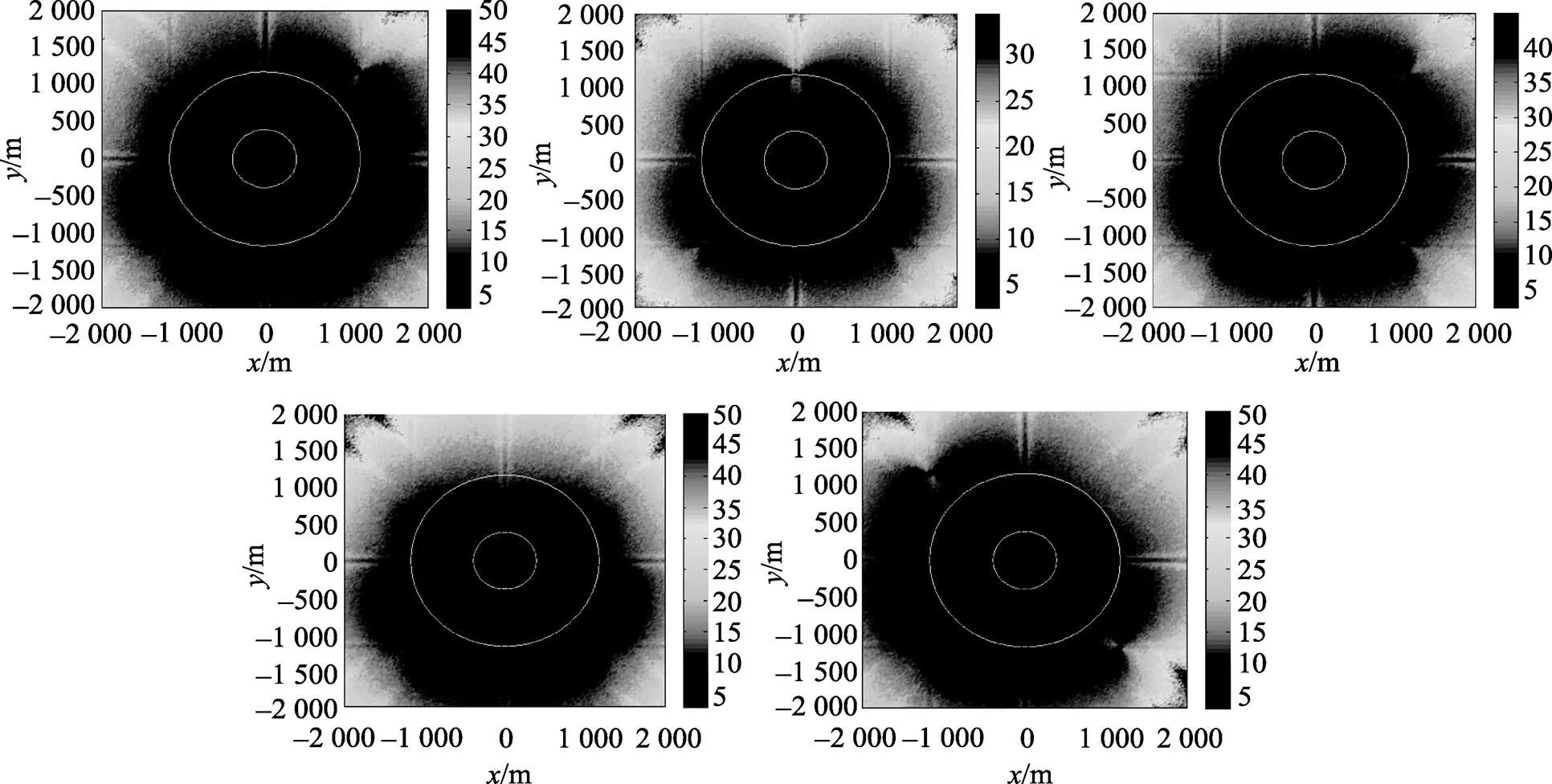
图6 缺少2~3个浮标时误差分布仿真结果

图7 缺少4个浮标时误差分布仿真结果

4 结束语

入水点测量浮标阵中心4个浮标在缺失1个的条件下对测量精度不造成影响, 测量浮标阵缺失2到3个浮标对测量精度也不造成影响; 缺失4个浮标且阵型不对称, 对测量精度迅速下降。在海上实际试验中, 如果缺失浮标数量及阵型大于以上最低条件, 为保证鱼雷入水点测量精度, 则应通报指挥部, 建议取消或延后发射鱼雷, 重新调整浮标, 为指挥决策提供技术支撑。

[1] 胡友峰. 非机动水下三维被动目标运动分析研究[D]. 西安: 西北工业大学, 2002.

[2] 时胜国, 杨德森. 基于矢量水听器的源定向理论及其定向误差分析[J]. 哈尔滨工程大学学报, 2003, 24 (2): 132-135.Shi Sheng-guo, Yang De-sen. Acoustic Source Location by Acoustic Vector-sensor and Its Bearing Error[J]. Journal of Harbin Engineering University, 2003, 24 (2): 132- 135.

[3] 詹艳梅. 纯方位目标运动分析方法研究[D]. 西安: 西 北工业大学, 2001.

Error Analysis of Measuring Water Entry Point for Rocket-Assisted Torpedo

ZHANG Yu-Tao, XUE Fei, LI Peng

(91439thUnit, The People′s Liberation Army of China, Dalian 116041, China)

Absence of buoys used for hydroacoustic localization in sea trial may reduce measurement accuracy of water entry point of a rocket-assisted torpedo. In this paper, the preset buoy array for measuring water entry point of a rocket-assisted torpedo is simulated with the software Matlab, and the effect of absence of some buoys on measurement accuracy of water entry point is analyzed. The results show that when absent buoys and buoy array reach to the lower limit, i.e. 4 of 12 buoys are absent and the buoy array is asymmetric, the measurement accuracy will decrease rapidly. Therefore, if the topology of preset buoy array does not satisfy the lower limit, the array must be adjusted.

rocket-assisted torpedo; measurement accuracy; hydroacoustic localization; buoy array; simulation

TJ631.2; TM46

A

1673-1948(2012)05-0392-04

2011-11-15;

2012-03-05.

张玉涛(1981-), 男, 工程师, 主要从事试验装备指挥和技术保障工作.

(责任编辑: 陈 曦)