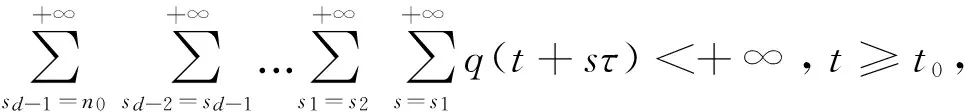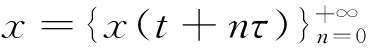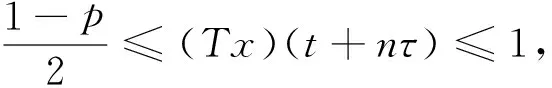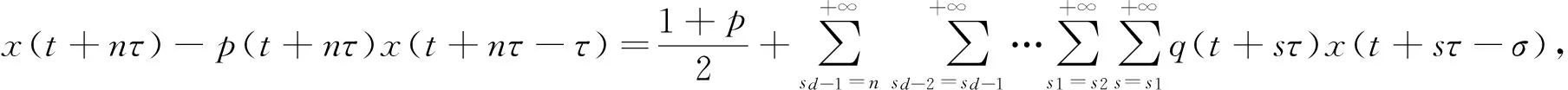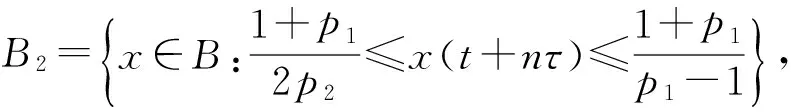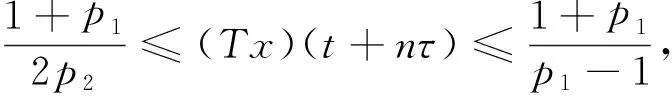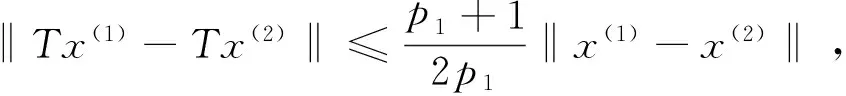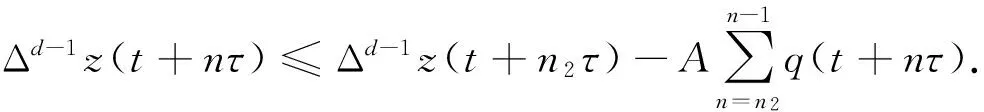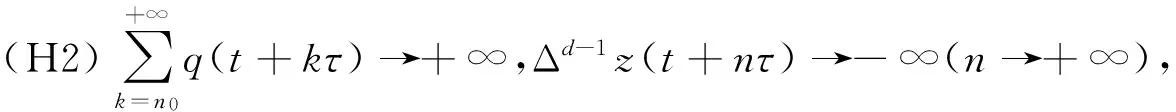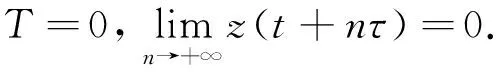具有连续变量高阶差分方程的振动性

赵玉萍

(青海民族大学 数学学院 青海 西宁 810007)

0 引言

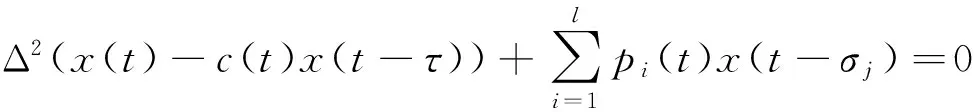
本文研究具有连续变量的高阶差分方程

Δd(x(t)-p(t)x(t-τ))+q(t)x(t-σ)=0, 0

(1)

解的振动性. 其中Δx(t)=x(t+τ)-x(t)，τ>0是步长,d≥1是奇数，σ>0是给定的,p(t)∈C([t0,+∞),R),q(t)∈C([t0,+∞),[0,+∞)).

1 基本引理

引理1[5]假设d≥1是整数,z(t+nτ)是实数列, 如果Δdz(t+nτ)最终定号, (即当n充分大后恒有Δdz(t+nτ)>0或有Δdz(t+nτ)<0), 则Δiz(t+nτ)最终严格单调且定号i=0,1,…,d-1.

引理2[5]假设d≥1是奇数，z(t+nτ)是正实数列且有界，Δdz(t+nτ)最终为负, 则最终有Δdz(t+nτ)≥Δz(t+nτ).

引理3[6]假设d≥1是奇数，z(t+nτ)是负的实数列, Δdz(t+nτ)最终为负, 则Δz(t+nτ)<0.

引理4[6]假设d≥1是奇数,z(t+nτ)是正的实数列, 且Δdz(t+nτ)最终为负, 则Δd-1z(t+nτ)>0.

2 主要结果

证明取充分大n1，n1≥n0，t>t0，使得

(2)

T是连续的，对∀x∈B1(n≥n1)有

证明证明类似于定理1，取充分大n1，n1≥n0，t>t0，使得

(3)

x(t)就是方程(1)的一个有界的最终正解.

定理3设0

(H1)存在函数y(u)∈C(R,R),使得x(u)≥y(u),uy(u)>0(u≠0),且y(u)≥m>0,m是常数;

则方程(1)的解振动.

证明反证法. 设方程(1)具有非振动解，不失一般性，设x(t)是最终正解. 令z(t)=x(t)-p(t)x(t-τ)，则方程(1)可变形为Δdz(t)+q(t)x(t-σ)=0，则z(t)>0.

事实上，Δdz(t)=-q(t)x(t-σ)<0, 由引理1知，z(t)>0或z(t)<0. 如果z(t)<0，则z(t+nτ)<0，由引理3，Δz(t+nτ)<0. 于是n≥n1,z(t+nτ)≤z(t+n1τ)<0, 因此x(t+nτ)≤z(t+n1τ)+p(t+nτ)x(t+nτ-τ)≤z(t+n1τ)+x(t+nτ-τ),n≥n1.

Δz(t+nτ) ≤Δdz(t+nτ)

≤-y(t+nτ-σ)q(t+nτ)

≤-mq(t+nτ)z(t+nτ)

由条件(H2)z(t+nτ)→-∞(n→+∞). 这与z(t+nτ)>0矛盾.所以方程(1)的解振动.

参考文献：

[1] 李同兴，韩振来，张萌，等. 一类具有连续变量的二阶非线性中立型时滞差分方程的振动性[J]. 山东大学学报: 理学版, 2008, 43(2): 70-72.

[2] 刘一龙，杨甲山. 一类二阶超线性中立型时滞差分方程的有界振动性[J]. 郑州大学学报:理学版，2008, 40(2):24-28.

[3] 何严生, 俞元洪. 二阶非线性差分方程的振动定理[J]. 数学研究与评论, 2004, 24(4): 740-744.

[4] 张晓建，刘兴元. 非线性二阶中立型差分方程的振动性[J]. 四川师范大学学报:自然科学版, 2008, 31(2):176-178.

[5] 唐清, 干曾玲. 高阶中立型差分方程的振动性及其非振动解的渐近性态[J]. 数学杂志, 2000, 20(2)：207-210.

[6] 张晓建, 杨甲山. 奇数阶非线性中立型差分方程的振动性[J]. 河南师范大学学报:自然科学版, 2009,37(2): 18-20.