互质因子摄动系统的非脆弱控制

孟新宇，宁 辉，王道波，王西超

（1.南京航空航天大学 自动化学院，南京210016；2.西北核技术研究所，乌鲁木齐841700）

控制系统的鲁棒稳定性是指按标称系统设计的控制器，能使摄动后的系统在某种度量意义下，其附近的一族系统均稳定。在目前大部分相关文献中，通常仅对被控对象摄动情况下的闭环系统的鲁棒稳定性进行了分析［1－2］。然而，在实际问题中，由于元件老化、参数漂移等多种因素，控制器本身的摄动也是不可避免的。众所周知，系统的各项性能指标在摄动情况下不一定能够维持，因此，近年来系统的性能指标对摄动的敏感性、鲁棒稳定性以及非脆弱性等问题，已逐渐成为国内外学者理论研究的热点，并已初步取得一些研究成果［3－4］。在众多研究方法中，互质因子摄动描述已被证明是一种有用的不确定性描述方法，它允许摄动后的系统与标称系统有不同的不稳定极点和不稳定极点的数目，且不需要对被控对象和控制器作某些附加的假设，因此研究互质因子摄动系统的非脆弱鲁棒性问题，更具普遍意义［5－7］。另外，工程上要求系统应有良好的干扰抑制能力，而灵敏度正反映了系统对干扰的敏感性。本文运用该方法，对系统对摄动的灵敏度、鲁棒稳定性及非脆弱性进行讨论。

1 问题描述

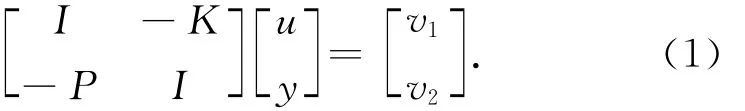
当矩阵

考虑图1所示的标称反馈系统，不难得出

图1 反馈系统

可逆时，方程（1）有唯一解，称系统（1）是适定的。图1反馈系统适定的充分条件是P（s）为严格真的。假定P（s）满足严格真的条件，则由式（1）得

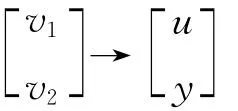
的闭环传递函数为

称S（P，K）＝（I－KP）－1为系统的灵敏度函数矩阵，它反映了系统对外部干扰的敏感性。

对P（s）和K（s）作双互质分解

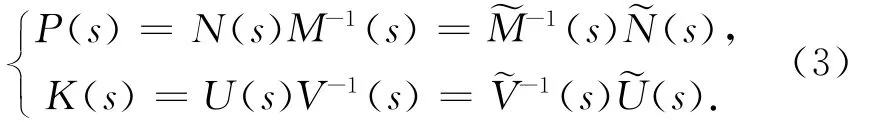
在以下讨论中均要求K（s）能镇定P（s），即有H（P，K）∈RH∞，从而可推断出灵敏度函数矩阵S（P，K）∈RH∞。设灵敏度函数矩阵S（P，K）和闭环传递函数阵H（P，K）的H∞范数满足以下约束：

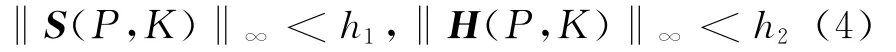
式中，hi（i＝1，2）为正常数。

与标称系统相对应，分别用SΔ、HΔ、PΔ、KΔ表示摄动系统的灵敏度函数矩阵、闭环传递函数矩阵、被控对象传递函数和控制器传递函数。

本文所讨论的非脆弱鲁棒稳定性问题，就是对系统（1）有式（3）所示的双互质分解，在互质因子均存在摄动的情况下，使得摄动系统灵敏度函数矩阵SΔ和闭环传递函数阵HΔ均仍保持稳定，且其H∞范数保持在有限范围内。

2 相关引理

引理1［1］设Δ∈RH∞，若‖Δ‖∞＜1，则有

引理2［1］若P（s）和K（s）有式（3）所示的双互质分解，且系统是能够稳定的，则可以选择稳定的矩阵M，N，˜M，˜N，U，V，˜U，˜V，使下式成立

引理3［3］设标称系统（P，K）是稳定的，且有稳定的右互质分解P＝NM－1，K＝UV－1，则对于被控对象和控制器的摄动族

σ（·）表示最小奇异值。

3 主要结果

由引理3可得如下推论：

推论1 设标称系统（P，K）是稳定的，且有稳定的左互质分解P＝˜M－1˜N，K＝˜V－1˜U，则对于被控对象和控制器的摄动族

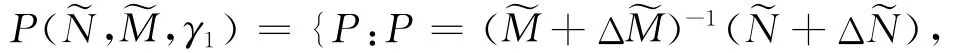
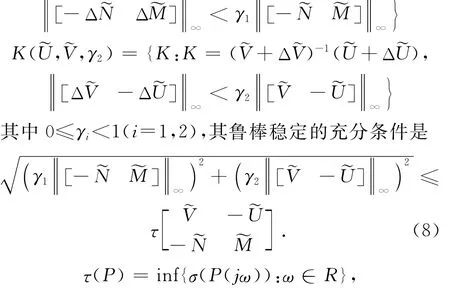
σ（·）表示最小奇异值。

证明过程与引理3的证明过程类似，此略。

定理1 考虑图1所示的标称反馈系统，设被控对象P有右互质分解P＝NM－1，控制器K有左互质分解K＝˜V－1˜U，且满足式（6），假定P和K存在互质因子摄动ΔM，ΔN，Δ˜U，Δ˜V∈RH∞，若满足以下两个条件：

式中，0≤α1＜1.

则有：

1）灵敏度函数摄动矩阵

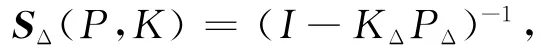
保持稳定，且满足

2）闭环传递函数摄动矩阵HΔ（P，K）保持稳定，且满足

很显然，由式（6）得˜VM－˜UN＝I.令

再由引理1得（I＋Δ1）－1∈RH∞，又因为

则由式（4）与定理条件得

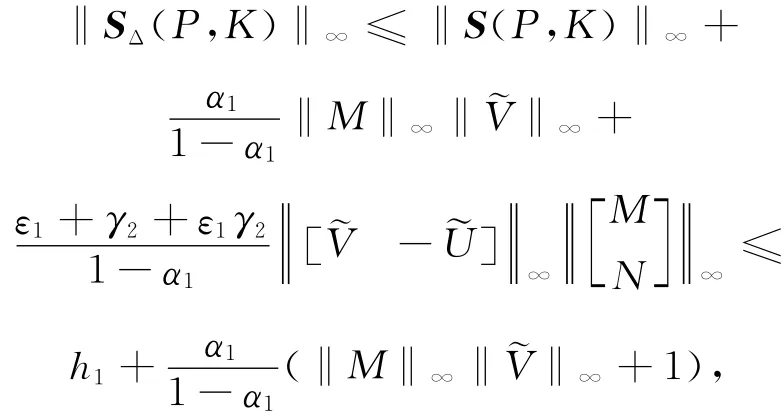
同理可推出

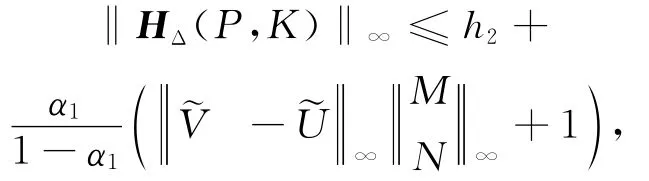
证毕。该定理对被控对象右互质分解和控制器左互质分解情况进行分析，分别得出了灵敏度函数摄动矩阵和闭环传递函数摄动矩阵与原标称矩阵之间的关系，及其在能稳定条件下H∞范数所满足的条件。类似地，在被控对象左互质分解和控制器右互质分解情况下，可得如下推论：

推论2 考虑图1所示的标称反馈系统，设被控对象P有左互质分解P＝˜M－1˜N，控制器K有右互质分解K＝UV－1，且满足式（6）假定P和K 存在互质因子摄动Δ˜M，Δ˜N，ΔU，ΔV∈RH∞，若满足以下两个条件：

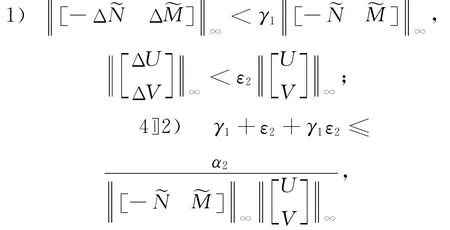
式中，0≤α2＜1.

则有：1）灵敏度函数摄动矩阵

证明过程与定理1类似，此略。以上分别对两种摄动情况下系统的非脆弱鲁棒稳定性作了讨论，这两种情况之间的关系在下面的定理给出了回答。

定理2 图1所示的标称反馈系统，被控对象P和控制器K 有式（3）所示的稳定的双互质分解，若其摄动族均能满足定理1和推论2，则有又因为

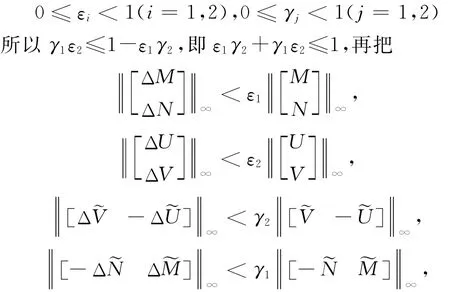
代入得证。

4 结论

1）在推导过程中，引入了一个常数0≤αi＜1（i＝1，2）来衡量互质因子摄动的程度，如果αi＝0（i＝1，2），则有εi＝γi＝0（i＝1，2），即系统不存在任何摄动；

2）如果被控对象P和控制器K的摄动是单独出现的，只需在上述定理中令εi＝0（i＝1，2）或γi＝0（i＝1，2）便可得到相应的结果；

3）不论被控对象P和控制器K的摄动程度如何，还是单独出现摄动，均满足定理2的内容。

研究了被控对象和控制器均存在互质因子摄动时，闭环系统的非脆弱鲁棒稳定性问题，并相应地给出了两类情况下的充分条件，并对两类情况之间的关系作进一步研究，为互质因子摄动下鲁棒控制器的研究与设计问题提供了基础。

［1］ Gu G X，Qiu L.Connection of multiplicative／relative perturbation in coprime factors and gap metric uncertainty［J］.Automatica，1998，34（5）：603-607.

［2］ Catherine Bonnet，Jonathan R.Coprime factorizations and stability of fractional differential systems［J］.Systems ＆Control Letters，2000，41（3）：167-174.

［3］ 张高民，贾英民.基于互质因子摄动的反馈系统的鲁棒稳定性［J］.自动化学报，2002，28（6）：974-976.

［4］ Li Li，Fernando Paganini.Structured coprime factor model reduction based on LMIs［J］.Automatica，2005，41（1）：145-151.

［5］ Ruth F.Robustly stabilizing controllers with respect to left coprime factor perturbations for infinite dimensional linear systems［J］.Systems ＆ Control Letters，2006，55（7）：509-517.

［6］ Carolyn Beck.Coprime factors reduction methods for linear parameter varying and uncertain systems［J］.Systems ＆Control Letters，2006，55（3）：199-213.

［7］ Sokolov V F.Suboptimal robust synthesis for MIMOplant under coprime factor perturbations［J］.Systems ＆ Control Letters，2008，57（4）：348-355.