具有流体动力阻尼项的波动方程解的渐近行为
2012-05-15王宏伟郭红霞
王宏伟, 郭红霞
(1.新乡学院 数学系 河南 新乡 453003; 2.西安交通大学 理学院 陕西 西安 710049; 3.郑州大学 数学系 河南 郑州 450001)
0 引言
研究如下一类具有流体动力阻尼项的波动方程的Cauchy问题
utt-uxxt-uxx-H(uxxx)+uxxxx=f(u)xx,
(1)
u(0)=φ(x),ut(0)=ψ(x).
(2)
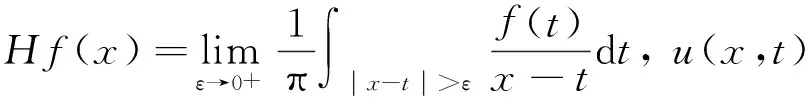
这类方程的研究与Boussinesq方程
utt-uxx+uxxxx=f(u)xx
(3)
有密切的联系. 方程(3)已有很多研究成果. Liu[2]讨论了方程(3)小初值整体解的渐近性质; Cho等[3]讨论了(3)在高维空间中小初值整体解的存在性; Linares在文献[4-5]中也研究了这类方程的整体解的长时间行为. 至于初值问题(1),(2), 尚未见到相关结果.
作者将研究问题(1),(2) 整体解的长时间行为. 通过对方程(1)的线性方程解的衰减估计, 利用压缩映射原理, 得出了整体解在小初值条件下的渐近性质.
1 线性方程的估计
考虑线性方程
utt-uxxt-uxx-H(uxxx)+uxxxx=gxx,
(4)
u(0)=φ(x),ut(0)=ψ(x).
(5)
由Fourier变换和Duhamel原理, (4)和(5)的解由下式给出
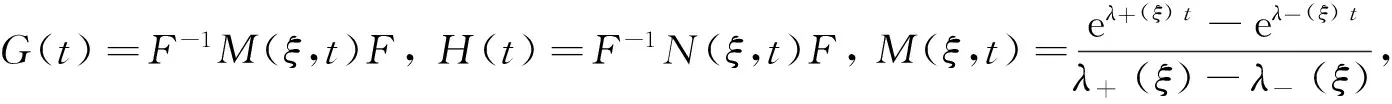

引理1如果k≥0,p∈[2,],q∈[1,2],r∈[1,2],γ≥0,则对有下列衰减估计
(6)
证明把λ±(ξ)代入M(ξ,t)的表达式, 有
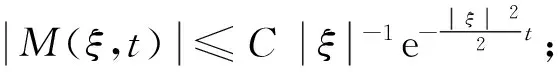
应用Hausdorff-Young不等式, 有
=I1+I2.
I1的估计是

I2的估计是

合并I1和I2的估计, 有(6)式成立.
引理2如果k≥0,p∈[2,],q∈[1,2],r∈[1,2],(当r=p=2时,m≥0),γ≥0, 则对有下列衰减估计
(7)


与引理1的证明类似, 可以得到(7).
引理3如果k≥0,p∈[2,],q∈[1,2],r∈[1,2],(当r=p=2时,m≥0),

(8)
利用(6),(7)和(8)三式, 得到如下线性方程(4),(5)解的存在唯一性定理.
定理1如果k≥0,p∈[2,],q∈[1,2],r∈[1,2],(当r=p=2时,m≥0),γ≥0,那么对则方程(4),(5)存在唯一解且下列衰减估计成立
2 整体解的渐近性质
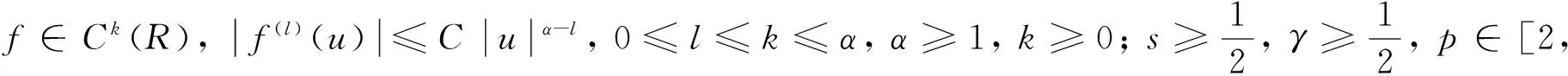
(9)
那么问题(1),(2)存在唯一解u(x,t)∈C([0,);且满足下列衰减性质
(10)
其中,ρ是一个依赖于f和δ的充分小的正数.
证明定义度量空间
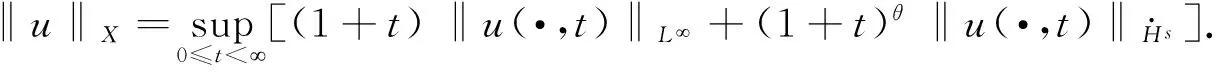
在定理1中取k=0,p=,q=1,r=2,m=s,则
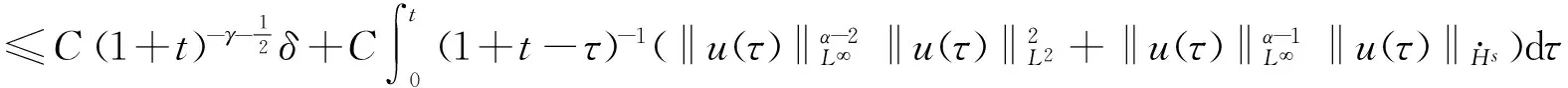
因为α+2θ-2≥α+θ-1≥1, 利用文献[6]的引理4.1, 有
(11)
在定理1中取k=s,p=2,q=1,r=2,m=0, 则
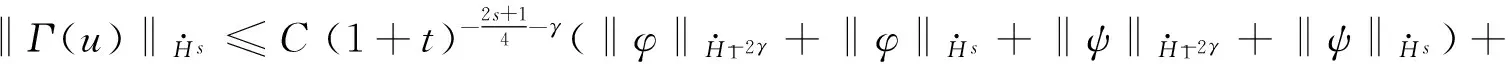
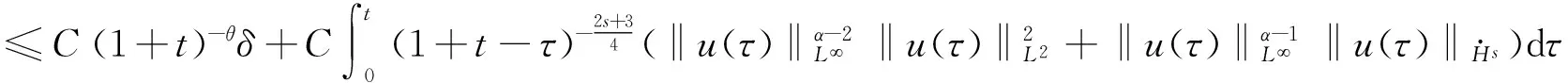
根据θ的定义, 有
(12)
由(11)和(12)两式, 得到‖Γ(u)‖X<ρ, 即Γ是X到X上的映射.
对u,v∈X, 由Γ(u)的表达式, 有
利用(11)和(12)两式的方法, 有
‖Γ(u)-Γ(v)‖X≤C(‖u‖X+‖v‖X)α-1‖u-v‖X≤Cρα-1‖u-v‖X.
即对充分小的ρ,Γ是压缩映射. 根据压缩映射原理,Γ(u)在X上有唯一的不动点u(x,t), 它是问题(1)和(2)的解, 且满足(10).
参考文献:
[1] Mingaleev S F, Gaididei Y B. Solitons in anharmonic chains with power-law long-range interactions[J]. Physical Review E, 1998, 58(3): 3833-3842.
[2] Liu Yue. Decay and scattering of small solutions of a generalized Boussinesq equation[J]. J Funct Anal, 1997, 147(1): 51-68.
[3] Cho Y, Ozawa T. On small amplitude solutions to the generalized Boussinesq equations[J]. Discrete Contin Dyn Syst, 2007, 17(4): 691-711.
[4] Linares F. Global existence of small solutions for a generalized Boussinesq equation [J]. Journal of Differential Equations, 1993, 106(2): 257-293.
[5] Linares F, Scialom M. Asymptotic behavior of solutions of a generalized Boussinesq equation[J]. Nonlinear Analysis TMA, 1995, 25(11): 1147-1158.
[6] Chen Guowang, Wang Shubin. Existence and nonexistence of global solutions for the generalized IMBq equation[J]. Nonlinear Anal, 1999, 36(8): 961-980.
