中心弱Armendariz环
2012-05-15解晓娟宋贤梅
解晓娟, 宋贤梅
(安徽师范大学 数学系 安徽 芜湖 241003)
0 引言
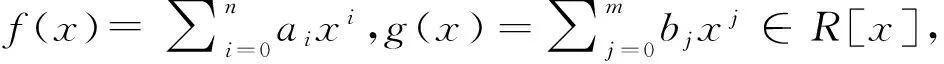
作者定义了新的环类,即中心弱Armendariz环,通过例子说明中心弱Armendariz环是弱Armendariz环的真推广,也是中心Armendariz环的真推广.因此,对中心弱Armendariz环的研究是有意义的.作者主要给出了中心弱Armendariz环的等价刻画;说明了中心弱Armendariz环与Abelian环以及p.p.-环的关系;证明了若R是半素环且R[x]/(x2)是中心弱Armendariz,则R是约化环;若R/I是中心弱Armendariz的且理想I是约化的,则R是中心弱Armendariz的.
1 主要结果
定义设R是环.对任意的f(x)=a0+a1x,g(x)=b0+b1x∈R[x],若f(x)g(x)=0,则对任意的i,j,有aibj∈C(R),那么称R是中心弱Armendariz环.
由定义易知,交换环、约化环、中心Armendariz环、弱Armendariz环和中心弱Armendariz环的子环都是中心弱Armendariz环.
例1存在一个环,是中心弱Armendariz环,但不是中心Armendariz环.
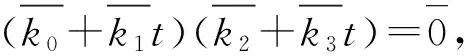
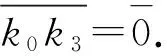
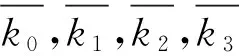
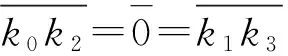
故R是弱Armendariz环.所以R是中心弱Armendariz环.
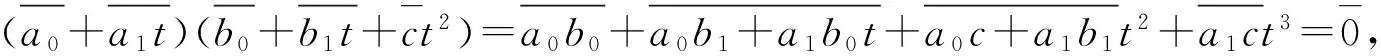
例2存在一个环,是中心弱Armendariz环,但不是弱Armendariz环.
设R=Z2[x,y]/(x2,y2),其中Z2是阶为2的Galois域,Z2[x,y]是Z2上关于可交换的未定元x,y的多项式环,(x2,y2)是由x2,y2生成的理想.
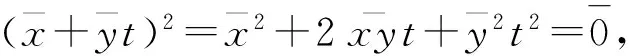
在文[2]和文[3]中,分别给出了中心Armendariz环和弱Armendariz环的等价刻画.下面给出中心弱Armendariz环的等价刻画.回忆R称为Abelian环,如果R的每个幂等元都在中心C(R)中[7].
定理1若R是环,则下列条件等价:
(1)R是中心弱Armendariz环;
(2)R是Abelian环,且对任意的幂等元e∈R,eR和(1-e)R是中心弱Armendariz环;
(3)存在中心幂等元e∈R,使得eR和(1-e)R是中心弱Armendariz环.
证明(1)⟹(2) 易知eR和(1-e)R是中心弱Armendariz的.下证R是Abelian的.
设e是R的幂等元,则对任意r∈R,令f(x)=e-er(1-e)x,g(x)=(1-e)+er(1-e)x∈R[x],则f(x)g(x)=0.由于R是中心弱Armendariz环,于是er(1-e)∈C(R),故er(1-e)=e[er(1-e)]=[er(1-e)]e=0,即er=ere.
类似地,令h(x)=(1-e)-(1-e)rex,t(x)=e+(1-e)rex∈R[x],则h(x)t(x)=0.于是(1-e)re=0,即ere=re.因此re=er.所以R是Abelian环.
(2)⟹(3)是显然的.
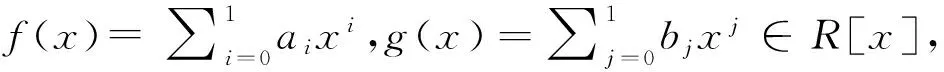
由条件(2)知,对任意的i,j,有eaiebj∈C(eR),(1-e)ai(1-e)bj∈C((1-e)R).
因为e∈C(R),(1-e)∈C(R),R=eR⊕(1-e)R.故aibj=eaibj+(1-e)aibj∈C(R).所以R是中心弱Armendariz环.
例3Abelian环未必是中心弱Armendariz环.
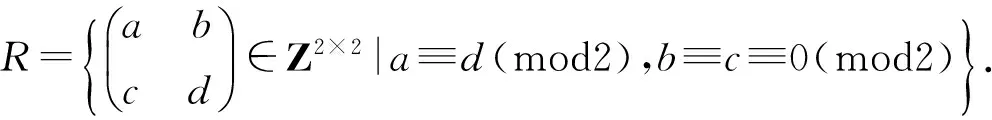
在文[7]中,环R称为右p.p.-环,如果R中元素的右零化子由幂等元生成.
定理2若环R是右p.p.中心弱Armendariz环,则R是弱Armendariz环.
证明由定理1可知,R是Abelian环.
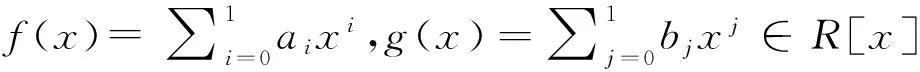
由于R是右p.p.-环,所以存在ei∈R,使得r(ai)=eiR,i=0,1.因此a0e0=0,b0=e0b0.对等式a0b1+a1b0=0两边同时右乘e0,有0=a0b1e0+a1b0e0=a0e0b1+a1e0b0=a1b0,于是a0b1=0.所以R是弱Armendariz环.
例4存在一个中心弱Armendariz环,既不是弱Armendariz环,也不是右p.p.-环.
设R=T(Z8,Z8).因为R是交换环,所以R是中心弱Armendariz环.
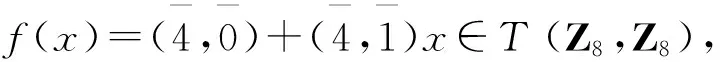
环R称为可逆的,如果对任意的a,b∈R,若ab=0有ba=0[8].
例5存在一个可逆环R,使得R的平凡扩张T(R,R)不是中心弱Armendariz环.
根据文[3],若R的约化环(即R中不含非零的幂零元),则R[x]/(x2)是弱Armendariz环,因此也是中心弱Armendariz的.在半素的条件下,有逆命题成立.
定理3设R是半素环.如果R[x]/(x2)是中心弱Armendariz环,则R是约化环.
证明设R是半素环,且S=R[x]/(x2)是中心弱Armendariz环.只需证明对任意r∈R且r2=0,有r=0即可.
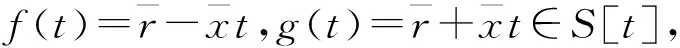
最后,考虑对环R,如果环R/I和理想I都是中心弱Armendariz,那么R是否是中心弱Armendariz环.例6说明一般情况下是不成立的,但是定理4证明了在I是约化的条件下,结论成立.
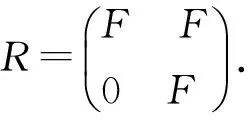
定理4设I是环R的约化理想,且R/I是中心弱Armendariz环,则R是中心弱Armendariz的.
证明设a,b∈R.若ab=0,则abI=0,于是(bIa)2=0.而I是约化的,故有bIa=0.注意到(aIb)3⊆(aIb)I(aIb)=0,因此aIb=0.
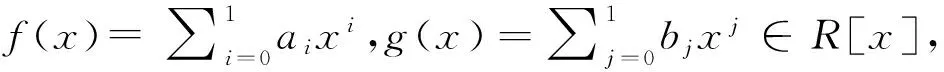
下证对任意的ai,bj,ajIbj=bjIai=0.
对等式a0b1+a1b0=0两边同时右乘Ib0,则有a0b1Ib0+a1b0Ib0=0.由于a0b1Ib0⊆a0Ib0=0,于是a0b1Ib0=0,进而a1b0Ib0=0.注意到(b0Ia1)3⊆(b0I)(a1b0Ia1b0)Ia1⊆(b0I)(a1b0Ib0)Ia1=0,故b0Ia1=0,进而a1Ib0=0.
对等式a0b1+a1b0=0两边同时左乘a0I,有a0Ia0b1+a0Ia1b0=0,于是a0Ia0b1=0,因此有(b1Ia0)3=0,于是b1Ia0=0,进而a0Ib1=0.所以aiIbj=bjIai=0.
参考文献:
[1] Rege M B, Chhawchharia S. Armendariz rings[J]. Proc Japan Acad: Ser A Math Sci, 1997, 73: 14-17.
[3] Jeon Y C, Kim H K, Lee Y, et al. On weak Armendariz rings[J]. Bull Korean Math Soc, 2009, 46(1): 135-146.
[4] Lee T E, Wong T L. On Armendariz rings[J]. Houston J Math, 2003, 29: 583-593.
[5] Kim N K, Lee Y. Armendariz rings and reduced rings[J]. J Algedra, 2000, 223: 477-488.
[6] Hong C Y, Kwak T K, Rizvi S T. Extensions of generalized Armendariz rings[J]. Algebra Collq, 2002, 30(2): 751-761.
[7] Armendariz E. A note on extensions of Baer and p.p.-rings[J]. J Austral Math Soc, 1974, 18:470-473.
[8] Kim N K, Lee Y. Extensions of reversible rings[J]. J Pure Appl Algebra, 2003, 185: 207-223.
