THE SLOP FLUX METHOD FOR NUMERICAL BALANCE IN USING ROE’S APPROXIMATE RIEMANN SOLVER*

WANG Dang-wei

State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China, E-mail: wangdw17@126.com

LIU Xiao-fang

Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China

Graduate University of the Chinese Academy of Sciences, Beijing 100049, China

CHEN Jian-guo, JI Zu-wen

State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China

THE SLOP FLUX METHOD FOR NUMERICAL BALANCE IN USING ROE’S APPROXIMATE RIEMANN SOLVER*

WANG Dang-wei

State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China, E-mail: wangdw17@126.com

LIU Xiao-fang

Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China

Graduate University of the Chinese Academy of Sciences, Beijing 100049, China

CHEN Jian-guo, JI Zu-wen

State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China

(Received August 12, 2011, Revised November 9, 2011)

Imbalance arises when the Roe’s method is directly applied in the shallow water simulation. The reasons are different for the continuity equation and the momentum equations. Based on the Roe’s method, a partial surface method is proposed for a perfect balance for the continuity equation. In order to generate a mathematically hyperbolic formulation, the momentum equations are split, which causes incompatibility in the calculation of the momentum equations. In this article a numerical approach named the Slop Flux Method (SFM) is proposed to balance the source terms and the flux gradient based on the finite volume method. The method is first applied to shallow water equations. The model is verified by analytical results of classical test cases with good agreement. Finally the method is applied to a steady flow simulation over a practical complicated topography and the result shows good balance and conservation.

shallow water simulation, Roe’s method, complicated topography, partial surface method, bed slop flux method

Introduction

The flows in rivers are very complex that failure often occurs in numerical simulations, especially, when there are shock waves involved[1]. For the equation system related with conservation laws, the Godunov-type methods can account for correct information in nearly all flow patterns even for cases including discontinuities by solving a set of Riemann problems over the entire computational domain. As the computational efficiency is too low when Riemann problems are solved directly, many approximate Riemann solvers are available that can provide good approximate results with much less computation time. The Roe’s method is one of the most robust approximate Riemann solvers widely used in aerodynamics and hydrodynamics. But difficulties still arise in solving the Riemann problems, especially, when the source terms are included in Shallow Water Equations (SWEs).

In order to keep the equations as a hyperbolic system and adopt the Roe’s method directly, the flux gradients and the source terms of SWEs are split artificially. Thus a numerical imbalance will be found for flows over natural riverbeds often with complicated topographies. It is understood that the imbalance is caused solely because of mathematical splitting[2]. This problem is usually treated in two different ways, namely, by the numerical method and by the mathematical method. Mathematical method involves revi-sing the formulation of the governing equations before any numerical algorithms to be implemented. Nugic[3]obtained SWEs in a revised mathematical formulation of the SWEs, by reallocating all bed-slope related flux gradients to the source terms. Rogers et al.[4]proposed an alternative splitting of the free surface gradient terms and derived a deviatoric form by subtracting an equilibrium solution that could refer to the still water conditions or the equilibrium conditions to allow one to drive a simulation to a steady state. Recently Liang[5,6]suggested another way for splitting free surface gradient terms to solve problems involving wetting and drying. On the other hand, the numerical methods make some revisions based on numerical algorithms without any change of the governing equations. Considerable progress was made in this direction[7-17]and the most representative work is Vázquez-Cendón’s[14]upwind scheme for the source terms, Zhou’s surface gradient method[15]and LeVeque’s[16,17]quasi-steady wave-propagation algorithm. Most of the above approaches are to keep a balance between the flux and the source terms in the motion equations but the conservative property of these approaches is usually not well addressed.

In this article we apply the Roe’s method to discretize the conservative form SWEs. For the imbalance thus caused, different techniques are proposed for the continuity equation and the momentum equations, separately. An approach of balancing the source terms with the flux is presented based on the finite volume method and it can be easily extended to other approximate Riemann solvers. Besides keeping a strict balance, the model established in this article has a good performance for conservation.

1. The nature of the problem

1.1 Governing equations

Neglecting the vertical acceleration of water particles and taking the pressure to be hydrostatic, the 2-D non-linear SWEs may be derived by depth-integrating the 3-D Reynolds averaged Navier-Stokes equations. In the matrix form, a conservation law of the 2-D non-linear shallow water equations can be written as

where U, F, G and S are the vectors representing the conserved variables, the numerical fluxes in x- and y-directions, and the source terms, respectively. Ignoring the viscous terms, the surface stress caused by the wind, and the Coriolis effects, these vectors can be written as

This is the popular form of the SWEs and it can be solved by Godunov-type schemes. In these expressions, h is the water depth, u and v are the depth averaged velocity in x- and y-directions, respectively, g is the acceleration due to the gravity,xs andys are the bed slopes in x- and y-directions, respectively, and are expressed as

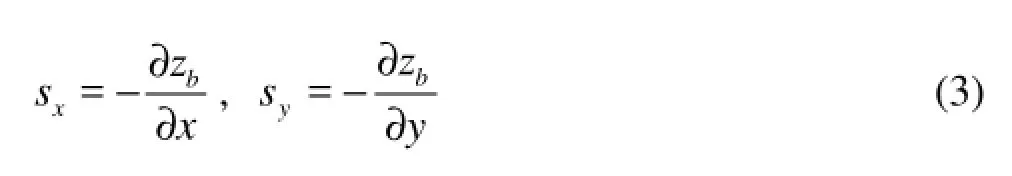
wherebz is the bed elevation,xf andyf are the bed friction due to the bed roughness in x- and y-directions, respectively and they can be estimated by empirical formulas as

where n is the Manning coefficient.

1.2 Discretizing by finite volume method The integral form of Eq.(1) is

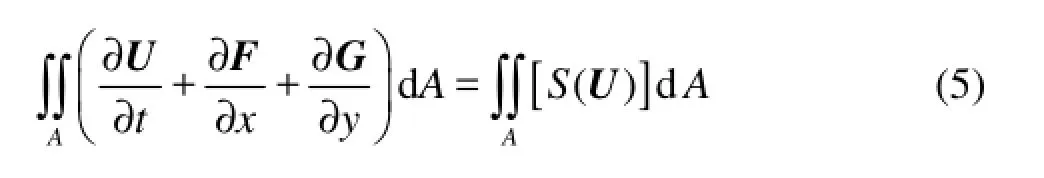
Applying Green’s theorem, Eq.(5) can be written as

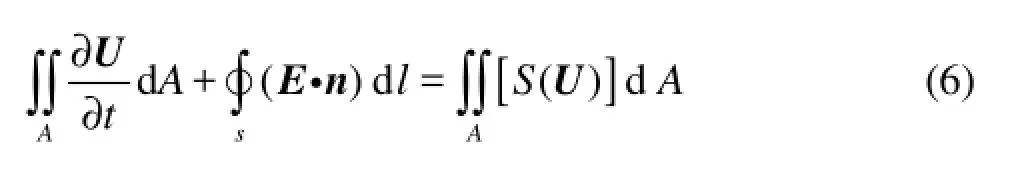
where E=(F, G), the n is the unit normal vectors of the cell boundary. The computational domain consists of quadrilateral cells and the variables are taken at the centre of each cell. So Eq.(3) becomes

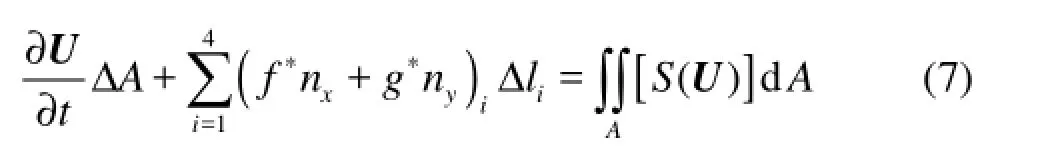
where AΔ is the area of the cell,ilΔ is the length of the boundary i,xn andyn are the Cartesian components of n in x- and y-directions, respectively, f∗and g∗denotes the numerical flux in x- and ydirections, respectively, which can be estimated by the Roe’s approximate Riemann solver as follows

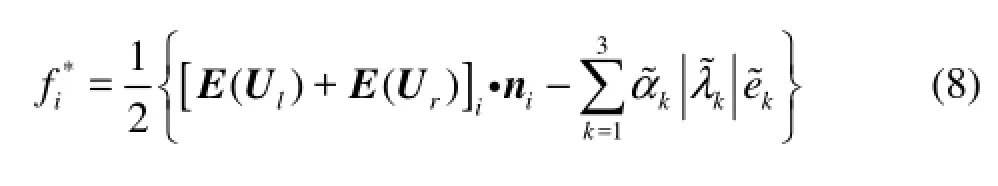
in whichlU andrU are the terms on the conservative left and right sides, separated by a discontinuity at the interface,andare the eigenvalue and the eigenvector of the linearized coefficient matrix of the SWEs. According to the principle of the Roe’s method, the linearized Jacobianfor Eq.(1) can be derived as

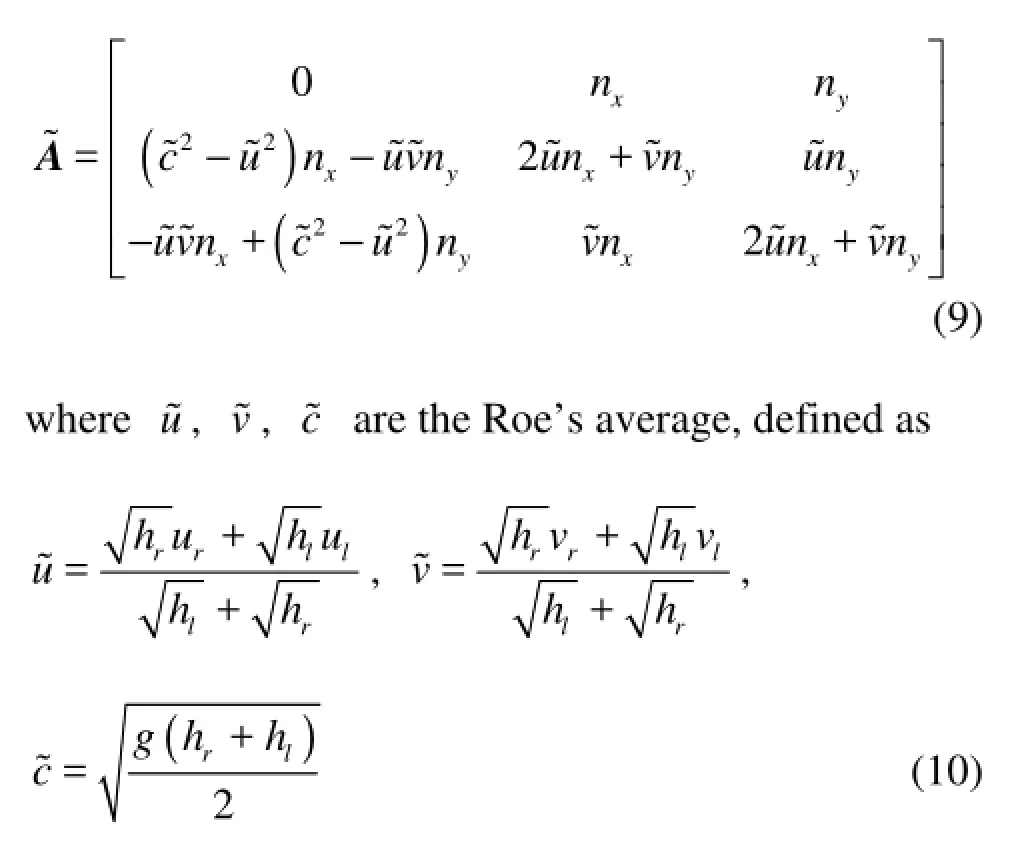
So the eigenvalues and eigenvectors ofare as follows

In the Roe’s method, the discontinuity at the interface of the computational element can be estimated by the eigen-decomposition algorithms as

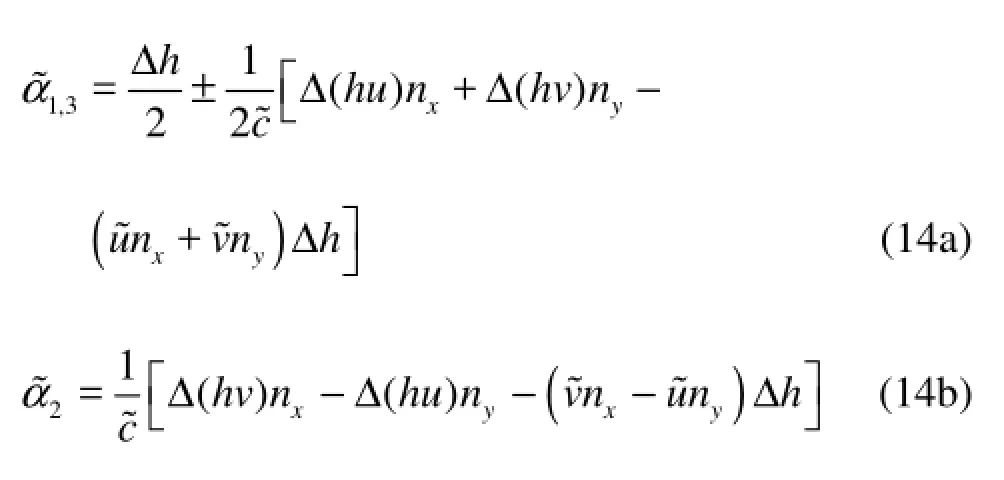
where ΔU is the jump value, or the difference between right and left Riemann states on either side of a cell interface of the variable U.

For a quiescent still water without any input, the values in SWEs should be u=v=0. Substituting Eqs.(10)-(14) into Eq.(7), the discretized form of the SWEs by the Roe’s method can be written as

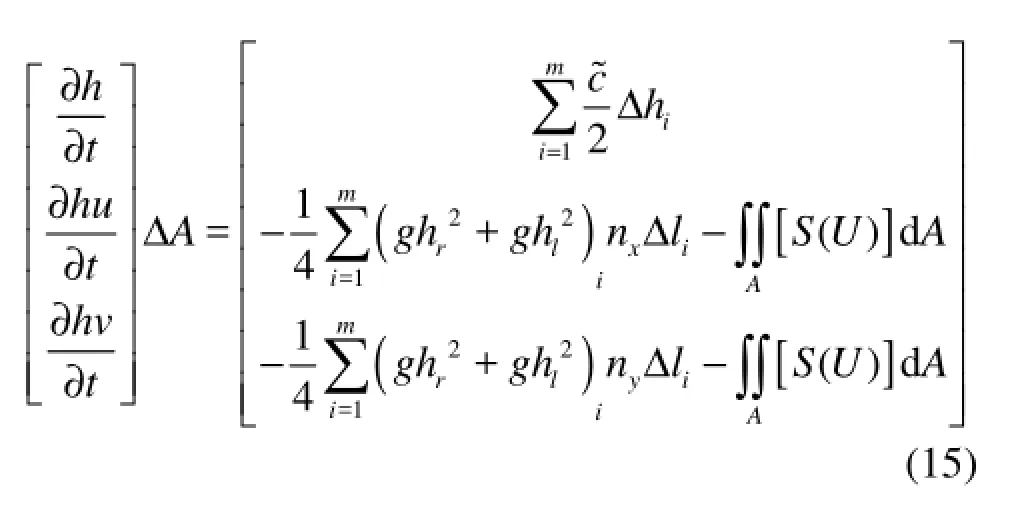
It is obvious that the water will keep quiescent if there is no inflow current and the variables would not change with time, so the right matrix must be equal to 0. Now the key is to keep the terms in the right matrix equal to 0.

1.3 Balancing methods

The imbalances of the continuity equation and the momentum equation are different and they need to be solved separately.

1.3.1 Partial surface method[18]for continuity equation

In the start, the water is still. Thus the continuity equation should satisfy the condition

But Eq.(16) does not always hold true. In fact, the condition of keeping Eq.(16) in equilibrium is so rigor for a riverbed that is rarely required in a natural environment and a flatterrain is one of conditions that may suit the needs. This problem is related to the physical nature of the Roe’s approximate Riemann solver. The Roe’s method is a kind of Godunov-type schemes, where the problem is treated as sets of Riemann problems over the entire computational domain, so the

jump value should be the driving force. From the physical point of view, the water movement is a kind of gravity wave, while hΔ is definitely not the original driving force for a gravity-driven flow like the water flow. It is obvious that the jump value of the water level would not drive the water from still to motion, so Eq.(16) should be

where z is the water level. Then the continuity equation should be written as

With no riverbed deformation, it can be easily shown that Eq.(18) becomes a typical continuity equation in 2-D SWEs. So Eq.(17) is correct both physically and mathematically and the imbalance caused by the continuity equation is thus eliminated.

1.3.2 Slop flux method for motion equations

For still water, the motion equations discretized by the Roe’s method (in x-direction, for example) is

The key is how to deal with the bed slope and the imbalance and the false flow caused by direct discretization. In order to solve this problem under the frame of FVM and keep the result conservative, the second term in Eq.(19) can be written as

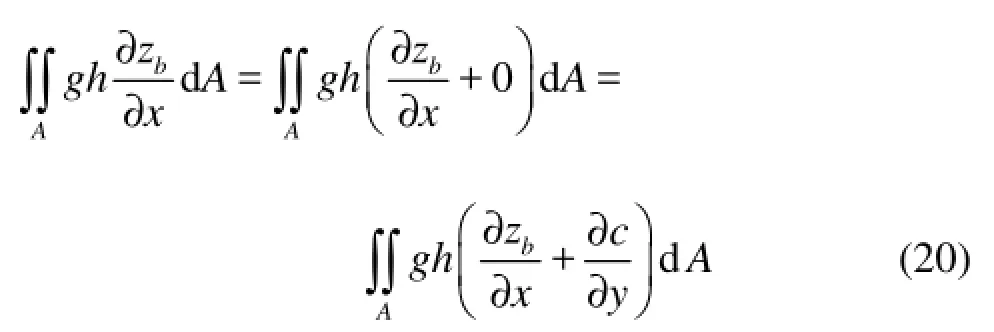
where c is a constant in a single cell. Applying Green’s theorem to the right side term of Eq.(20), we have

It can be considered as a Riemann problem, so Eq.(17) can be written as

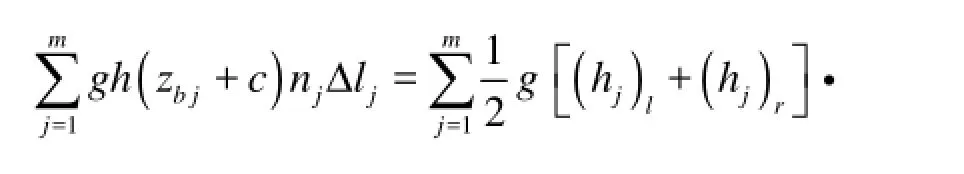
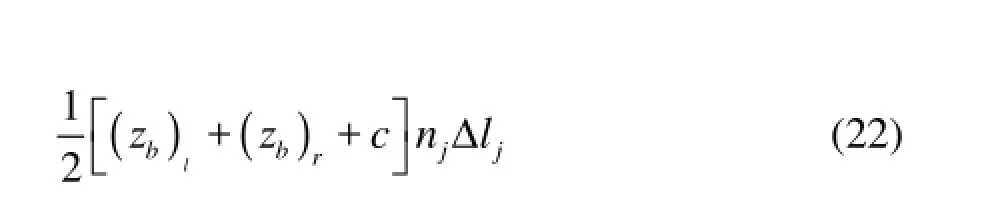
Now we need to calculate the value of c with the still water state as a boundary condition for this problem. In the still water state, we have

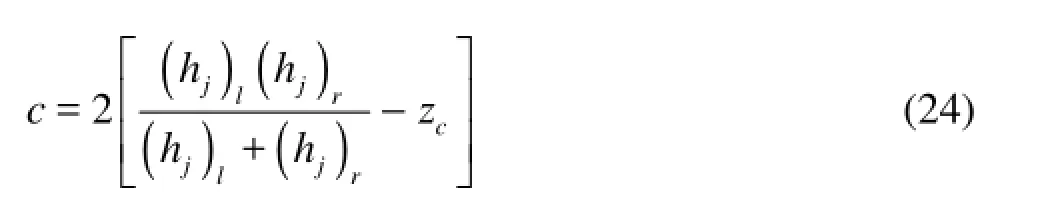
wherecz is the water level at the center of the cell. Substituting Eq.(24) into Eq.(22) we obtain the final discretization form of the bed slope in the source terms of the motion equations.

In view of stability and computational efficiency, the self-adaptable time step method[19]is adopt for solving the bed shear stress terms.

2. Results and discussion

The numerical scheme is validated against benchmark tests. The results are first compared with analytical solutions, then the model is applied in a practical flow simulation in Songhuajiang River with complicated natural topography. In all cases, g= 9.81m/s2.

2.1 Steady flow over a bump

The bed elevation of a 25 m long channel with a bump is defined by

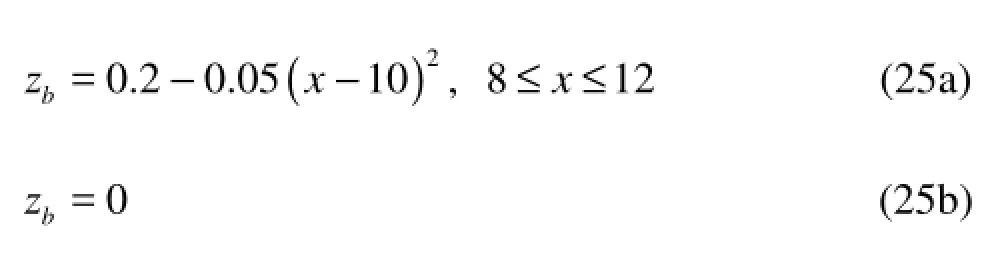
which is a classical test problem used as a benchmark test case for numerical methods at the workshop on dam-break wave simulations. A discharge per unit width of q=0.18 m2/s is imposed at the upstream boundary and h=0.33m is specified as the downstream boundary condition and the bed shear stress is ignored. In this case, the flow is trans-critical with a sGhoouctka l[w15a].ve and the analytical result was given by

The global relative error R is defined by

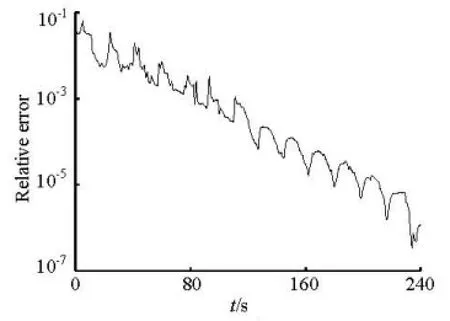
Fig.1 Convergence history of global error

Fig.2 Comparison of discharge

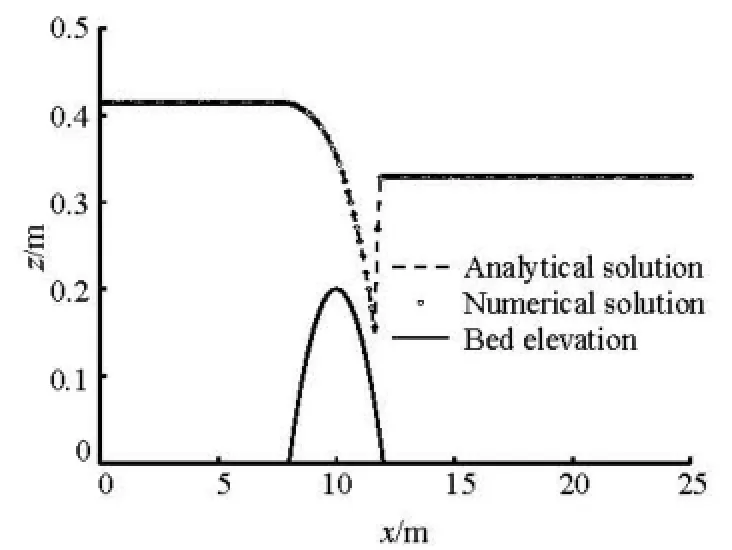
Fig.3 Comparison of water surface

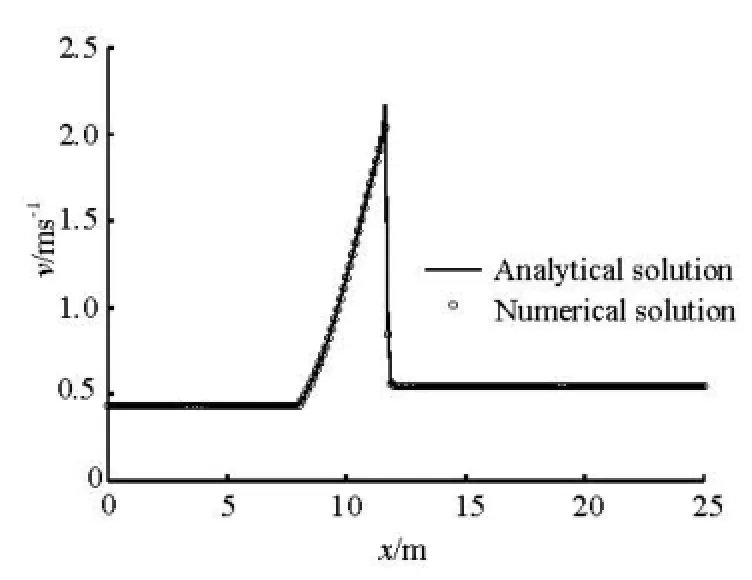
Fig.4 Comparison of velocity

Fig.5 Comparison of Froude number

2.2 Tidal wave flow over an irregular bed

绛蜡丛中一讲庐，披图想见过庭趋。埙篪韵事真馨逸，得许升堂展谒无。梓桥俯仰傍寒林，伴结幽芳夙抱深。家法岂惟传治谱，先将铁石炼胸襟。

This is a 1-D problem with bed topography defined by

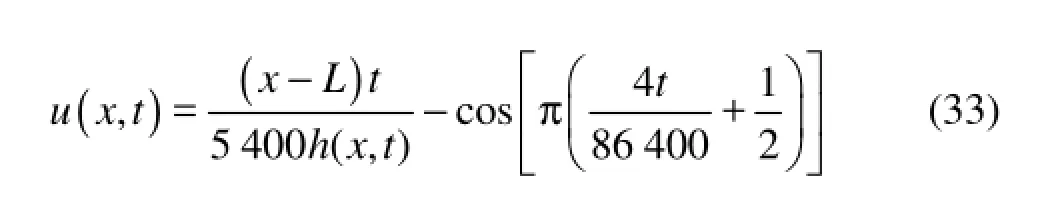
A comparison of the numerical results with the asymptotic analytical solution at t=7 552s is shown in Figs.6 and 7. The agreement is excellent especially for the water surface. The largest difference between the numerical and analytical values of the velocity is about 0.004 m/s. This suggests that the proposed scheme is accurate for tidal flow problems.

Fig.6 Comparison of water velocity

Fig.7 Comparison of water surface

2.3 Steady flow in Songhuajiang River with compli

cated bed topography

The model is used in Jiamusi reach of Songhuajiang River to evaluate the influence of building Liushudao dike on the flood control. The dike is built to protect people and animals on the island from flood disaster. The computational area is about 35 km2and the area of Liushudao Island is about 10 km2, as is shown in Fig.7. The whole computational domain is divided into 100×200 irregular quadrilateral grids. A discharge of 17 100 m3/s is imposed at the inlet and the corresponding water surface at the outlet is 79.290 m.

The relative error of discharge between inlet and outlet is defined as

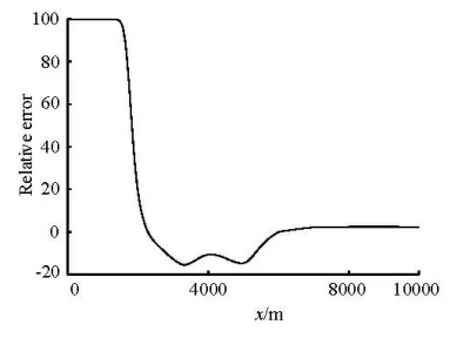
Fig.8 Convergence history ofDR

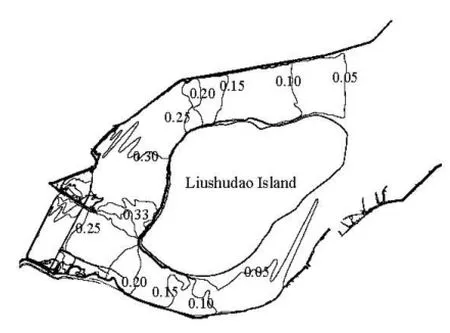
Fig.9 Change of water surface due to embankment around the island

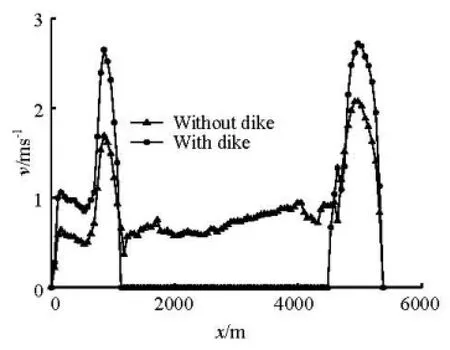
Fig.10 Velocity profile of a typical cross section

Figure 8 shows the convergence history of RDand RD=0.9% when the steady state is reached after 6 000 s. It shows that the model can keep variables conservative perfectly. Figure 9 shows the contour of the water surface change due to the Liushudao dike. In most area, the water surface rises when the Liushudao dike is built and this is because the water can not flow over the island as it did without the dike. The largest rise is about 0.33 m, which is near the inlet of the left branch because of an anti-flow there. Figure 10 shows the profile of the velocity of a typical cross section which goes across the island. Barred by theLiushudao dike, the water can not flood the island, where the velocity is decreased to 0 while the velocity in the main channel is increased.

3. Conclusion

This article presents a numerical model by solving 2-D SWEs using the Roe’s method. Imbalance would occur when the Roe’s method is directly applied to solve the SWEs, therefore, the partial surface method is proposed for balancing the continuity equations based on the physical nature of the Roe’s method. The source terms, especially, the bed slope term, often cause imbalance in the simulation of 2-D shallow water over complicated topography. In this article we propose a numerical method based on FVM to keep the conservative property of the conservation laws. The model is verified by results of classical test cases and the Songhuajiang River is taken as an example to show that the numerical model in this article enjoys generality, balance and conservation.

[1] YU Ming-hui, DENG Yin-ling and QIN Lian-chao et al. Numerical simulation of levee breach flows under complex boundary conditions[J]. Journal of Hydrodynamics, 2009, 21(5): 633-639

[2] ROGERS B. D., BORTHWICK A. G. L. and TAYLOR P. H. Mathematical balancing of flux gradient and source terms prior to using Roe’s approximate Riemann solver[J]. Journal of Computational Physics, 2003, 192(2): 422-451.

[3] NUGIC M. Efficient implementation of non-oscillatory schemes for the computation of free-surface flows[J]. Journal of Hydraulic Research, 1995, 33(1): 101-111.

[4] ROGERS B., FUJIHARA M. and BORTHWICK A. G. L. Adaptive Q-tree Godunov-type scheme for shallow water equations[J]. International Journal for Numerical Methods in Fluids, 2001, 35(3): 247-280.

[5] LIANG Q., BORTHWICK A. G. L. Adaptive quadtree simulation of shallow flows with wet–dry fronts over complex topography[J]. Computers and Fluids, 2009, 38(2): 221-234.

[6] LIANG Qiuhua. A coupled morphodynamic model for applications involving wetting and drying[J]. Journal of Hydrodynamics, 2011, 23(3): 273-281.

[7] AUDUSSE E., BOUCHUT F. and BRISTEAU M. O. et al. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows[J]. Journal of Scientific Computation, 2004, 25(6): 2050-2065.

[8] VALIANI A., BEGNUDELLI L. Divergence form for bed slope source term in shallow water equations[J]. Journal of Hydraulic Engineering, 2006, 132(7): 652-665.

[9] TORNBERGA A. K., ENGQUIST B. Numerical approximations of singular source terms in differential equations[J]. Journal of Computational Physics, 2004, 200(2): 462-488.

[10] LIANG Q., MARCHE F. Numerical resolution of wellbalanced shallow water equations with complex source terms[J]. Advances in Water Resources, 2009, 32(6): 873-884.

[11] XING Y., SHU C. A new approach of high order well-balanced finite volume WENO schemes and discontinuous Galerkin methods for a class of hyperbolic systems with source terms[J]. Communications in Computational Physics, 2006, 1(1): 100-134.

[12] BEGNUDELLI L., BRETT F. S. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying[J]. Journal of Hydraulic Engineering, 2006, 132(4): 371-384

[13] NOELLEA S., XING Y. and SHU C. High-order wellbalanced finite volume WENO schemes for shallow water equation with moving water[J]. Journal of Computational Physics, 2007, 226(1): 29-58.

[14] GARCÍA-NAVARRO P., VÁZQUEZ-CENDÓN M. E. On numerical treatment of the source terms in the shallow water equations[J]. Computers and Fluids, 2000, 29(1): 951-979

[15] ZHOU J. G., CAUSON D. M. and MINGHAM C. G. et al. The surface gradient method for the treatment of source terms in the shallow-water equations[J]. Journal of Computational Physics, 2001, 168(1): 1-25.

[16] LEVEQUE R. J. Finite volume methods for hyperbolic problems[M]. Cambridge, UK: Cambridge University Press, 2002.

[17] BALE D. S., LEVEQUE R. J. and MITRAN S. et al. A wave propagation method for conservation laws and balance laws with spatially varying flux functions[J]. Journal on Scientific Computing, 2002, 24(3): 955-978.

[18] WANG Dang-wei, YU Ming-hui and CHEN Jian-guo et al. Improve on WENO-Roe method for simulation of shallow water with complicated topography[J]. Chinese Journal of Applied Mechanics, 2011, 28(3): 249-253(in Chinese).

[19] WANG Xin, CAO Zhi-xian and YUE Zhi-yuan. Numerical modeling of shallow flows over irregular topography[J]. Journal of Hydrodynamics, Ser. A, 2009, 24(1): 56-62(in Chinese).

10.1016/S1001-6058(11)60219-9

* Project supported by the National Basic Research and Development Program of China (973 Program, Grant No. 2011CB409901), the Special Funds for Public Welfare Project (Grant No. 200901014), and the “12th Five-Year Plan” to Support Science and Technology Project (Grant No. 2012BAB02B01).

Biography: WANG Dang-wei (1982-), Male, Ph. D., Engineer

2012,24(1):58-64